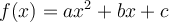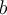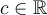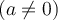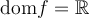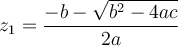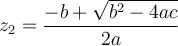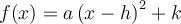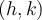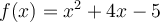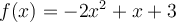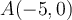2.2 Les fonctions algébriques
- Fonction linéaire (droite)
- Fonction quadratique (parabole)
- Fonction puissance (exposant naturel)
- Fonction rationnelle
- Fonction racine et exposant fractionnaire
- Trouver le domaine d'une fonction algébrique
2. Fonction quadratique (parabole)
Le graphique de la fonction est représenté par une parabole. À partir du graphique GeoGebra suivant, étudions plus en détail la fonction quadratique afin d'observer plusieurs de ses caractéristiques.
-
L'orientation de la parabole est déterminée par le paramètre
 .
.Son ouverture est vers le haut si
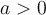 et vers le bas si
et vers le bas si 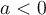 .
. Déplacez le curseur « a » afin de remarquer l'effet sur l'ouverture de la parabole pour différentes valeurs de
Déplacez le curseur « a » afin de remarquer l'effet sur l'ouverture de la parabole pour différentes valeurs de  .
.  Cochez la case Ordonnée. L'ordonnée à l'origine est le point
Cochez la case Ordonnée. L'ordonnée à l'origine est le point 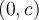 .
.
Déplacez le curseur « c » afin de remarquer l'effet sur le graphique pour différentes valeurs de
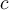 . La parabole se déplace parallèlement à l'axe des
. La parabole se déplace parallèlement à l'axe des  .
.-
 Cochez la case Sommet. Le sommet de la parabole est le point
Cochez la case Sommet. Le sommet de la parabole est le point 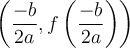 . En effet, il y a un axe de symétrie en
. En effet, il y a un axe de symétrie en 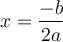 . Tout point de la parabole possède donc un deuxième point symétrique.
. Tout point de la parabole possède donc un deuxième point symétrique.En déplaçant le curseur « b », vous remarquez que l'axe de symétrie se déplace, mais que la distance entre les points symétriques reste la même. De plus, si
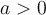 , le sommet est un minimum et si
, le sommet est un minimum et si 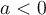 , le sommet est un maximum.
, le sommet est un maximum. - Les zéros de la parabole sont les solutions de l'équation
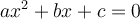 . On peut trouver, s'ils existent, les zéros de la fonction par la formule quadratique
. On peut trouver, s'ils existent, les zéros de la fonction par la formule quadratique 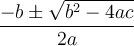 ou par la factorisation.
ou par la factorisation.
On appelle le discriminant
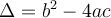 . Il aide à déterminer le nombre de zéros que possède la fonction.
. Il aide à déterminer le nombre de zéros que possède la fonction.  Cochez la case Zéro(s) et déplacez les différents curseurs « a », « b » et « c ».
Cochez la case Zéro(s) et déplacez les différents curseurs « a », « b » et « c ».-
Si
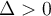 , la fonction possède deux zéros,
, la fonction possède deux zéros,  et
et 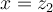 tels que
tels queOn peut exprimer la fonction en factorisant le polynôme sous la forme
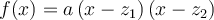 .
. Ex. : Choisissez a = 2, b = 3 et c = -5. Les zéros de la parabole sont
Ex. : Choisissez a = 2, b = 3 et c = -5. Les zéros de la parabole sont 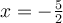 et
et 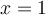 . En factorisant, on obtient
. En factorisant, on obtient 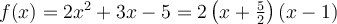 . Le discriminant
. Le discriminant 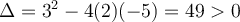 .
. -
Si
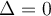 , la fonction possède un zéro
, la fonction possède un zéro  situé au sommet de la parabole.
situé au sommet de la parabole.On peut exprimer la fonction en factorisant le polynôme sous la forme
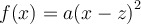 .
. Ex. : Choisissez a = 1, b = -6 et c = 9. La parabole possède un seul zéro en
Ex. : Choisissez a = 1, b = -6 et c = 9. La parabole possède un seul zéro en 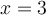 . En factorisant, on obtient
. En factorisant, on obtient 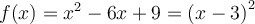 . Le discriminant
. Le discriminant 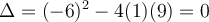 .
. -
Si
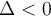 , la fonction ne possède aucun zéro. On ne peut factoriser le polynôme
, la fonction ne possède aucun zéro. On ne peut factoriser le polynôme 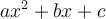 .
. Ex. : Choisissez a = 1 et b = 2. En déplaçant le curseur « c », on a que pour les valeurs
Ex. : Choisissez a = 1 et b = 2. En déplaçant le curseur « c », on a que pour les valeurs 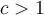 , la parabole ne possède aucun zéro. En effet, le discriminant
, la parabole ne possède aucun zéro. En effet, le discriminant 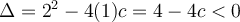 si
si 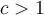 .
.
-
L'équation d'une parabole peut aussi être exprimée sous la forme canonique. Cette forme sera explorée plus en détails à partir du graphique GeoGebra dans la section des fonctions puissances.
On peut tracer le graphique d'une fonction quadratique à partir des éléments précédents. Voici quelques exemples.