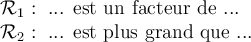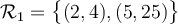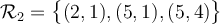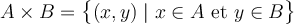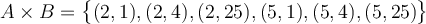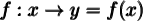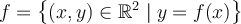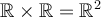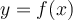2.1 Les fonctions
- Relation et fonction
- Domaine et image
- Graphique d'une fonction
- Points d'intersection avec les axes
1. Relation et fonction
En mathématiques, on définit une relation lorsque les éléments d'un ensemble de départ 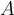 et d'un ensemble d'arrivée
et d'un ensemble d'arrivée 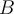 sont reliés par une loi quelconque
sont reliés par une loi quelconque 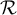 .
.
Exemple : Soit l'ensemble de départ 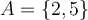 et l'ensemble d'arrivée
et l'ensemble d'arrivée 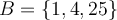 et les relations
et les relations
Ces relations peuvent être représentées par les diagrammes suivants :
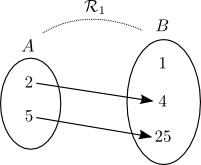
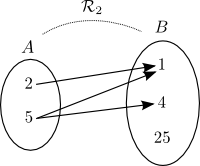
Chacune des relations est donc égale à l'ensemble des couples qui ont été formés entre les éléments des deux ensembles.
En fait, si on crée un ensemble contenant tous les couples 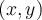 formés en prenant la première composante
formés en prenant la première composante  dans l'ensemble de départ
dans l'ensemble de départ 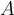 et la deuxième composante
et la deuxième composante  dans l'ensemble d'arrivée
dans l'ensemble d'arrivée 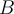 , on obtient ce qu'on appelle le produit cartésien de
, on obtient ce qu'on appelle le produit cartésien de 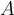 par
par 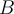 .
.
On le note :
Une relation 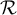 est en fait un sous-ensemble de
est en fait un sous-ensemble de 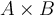 .
.
Dans notre exemple, 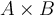 est un ensemble contenant 6 couples
est un ensemble contenant 6 couples 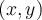 :
:
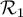 et
et 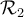 sont donc des sous-ensembles de
sont donc des sous-ensembles de 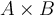 contenant chacun respectivement 2 et 3 couples.
contenant chacun respectivement 2 et 3 couples.
Certaines relations sont appelées fonctions. Pour cela, elles doivent posséder la caractéristique suivante :
Dans notre exemple, 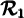 est une fonction, tandis que
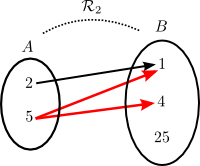
est une fonction, tandis que 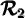 n'en est pas une puisque l'on y retrouve les couples
n'en est pas une puisque l'on y retrouve les couples 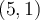 et
et 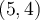 . En effet, dans le diagramme de
. En effet, dans le diagramme de 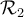 on remarque que l'élément
on remarque que l'élément 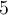 de l'ensemble
de l'ensemble 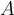 est relié à 2 éléments de l'ensemble
est relié à 2 éléments de l'ensemble 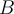 .
.
En général, nous nous intéressons aux fonctions réelles, c'est-à-dire aux fonctions dont les éléments de 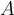 et
et 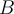 appartiennent à
appartiennent à 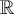 . De telles fonctions sont égales à un ensemble de couples ordonnés de nombres réels. Pour préciser les ensembles de départ
. De telles fonctions sont égales à un ensemble de couples ordonnés de nombres réels. Pour préciser les ensembles de départ 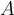 et d'arrivée
et d'arrivée 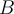 d'une fonction, on note
d'une fonction, on note 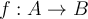 . Si l'on écrit
. Si l'on écrit 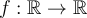 ,
,  est alors définie comme étant une fonction réelle.
est alors définie comme étant une fonction réelle.
La variable  se nomme la variable indépendante. On peut lui attribuer une valeur arbitraire choisie dans
se nomme la variable indépendante. On peut lui attribuer une valeur arbitraire choisie dans 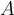 . Mais à partir du moment où la valeur de
. Mais à partir du moment où la valeur de  est déterminée, la valeur de
est déterminée, la valeur de  ou
ou 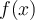 dépend de
dépend de  . On dit alors que
. On dit alors que  est la variable dépendante.
est la variable dépendante.