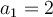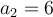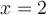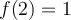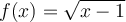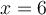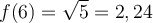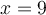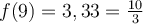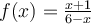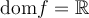2.3 Quelques fonctions particulières
- Fonction définie par parties ou par morceaux
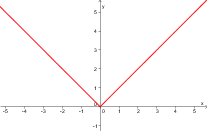
- Fonction valeur absolue
- Fonctions paires et impaires
1. Fonction définie par parties ou par morceaux
Les fonctions examinées dans les sections précédentes étaient toutes définies par une seule équation. Par contre, plusieurs phénomènes de la vie courante nécessitent plus d'une règle pour les définir.
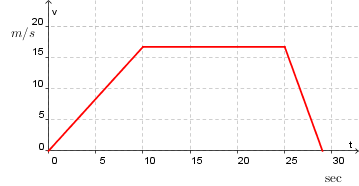
Le graphique suivant correspond à la vitesse d'une voiture variant en fonction de différents intervalles de temps. Durant les 10 premières secondes, la voiture a accéléré de manière uniforme pour atteindre une vitesse de 60 km/h (50/3 m/s). Elle a ensuite maintenu cette vitesse constante pendant 15 secondes, et à l'approche d'un feu rouge, elle a freiné de façon constante pendant 4 secondes jusqu'à un arrêt complet.
L'équation correspondant à cette situation est définie par
Pour évaluer la vitesse de la voiture à un temps 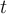 donné, nous devons déterminer auparavant à quelle partie du domaine appartient cette valeur. Par exemple :
donné, nous devons déterminer auparavant à quelle partie du domaine appartient cette valeur. Par exemple :
Si 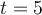 s., la vitesse de la voiture est
s., la vitesse de la voiture est 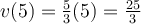 m/s ou 30 km/h, car
m/s ou 30 km/h, car ![5 \in \left[0, 10\right] 5 \in \left[0, 10\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f230a7e29506da9bd074f4623807762a.png) secondes.
secondes.
Si 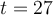 s., la vitesse de la voiture est
s., la vitesse de la voiture est 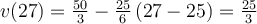 m/s ou 30 km/h, car
m/s ou 30 km/h, car ![27 \in \left[25, 29\right] 27 \in \left[25, 29\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/bc1b08a7098d2156f8538af2f4ed5d08.png) secondes.
secondes.
Un exemple classique d'une fonction définie par parties est la fonction valeur absolue. En effet, cette fonction est définie différemment selon que les valeurs sur son domaine sont positives ou négatives.
Comment déterminer le domaine d'une fonction définie par morceaux
Il faut d'abord se rappeler que le domaine d'une fonction algébrique est trouvé en respectant, entre autres, deux restrictions :
Pour déterminer le domaine d'une fonction définie par morceaux, il faut étudier la règle de la fonction pour chacun de ses sous-intervalles.
Par exemple, étudions plus en détail la fonction suivante :
Dans un premier temps, évaluons les images 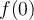 ,
, 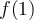 et
et 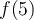 :
:
- Si
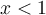 , la valeur de
, la valeur de 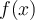 est
est 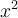 . Comme
. Comme 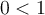 , on obtient que
, on obtient que 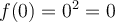 .
. - Si
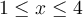 , la valeur de
, la valeur de 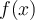 est
est 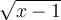 . Comme
. Comme ![1 \in \left[1, 4\right] 1 \in \left[1, 4\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/981491f647e62ea80161c49aef8d3b31.png) , on a que
, on a que 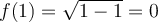 .
. - Si
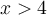 , la valeur de
, la valeur de 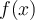 est
est 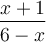 . Comme
. Comme 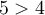 , on a que
, on a que 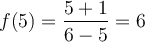 .
.
Si nous voulons maintenant déterminer le domaine de cette fonction, nous devons étudier la règle de correspondance pour chacun des trois sous-intervalles suivants : ![\left]-\infty, 1\right[ \left]-\infty, 1\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3fe97ae4b91d11cc8f6bcd108273a994.png) ,
, ![\left[1, 4\right] \left[1, 4\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d6756a3380c7423a8b9aa58fcff17a9a.png) et
et ![\left]4, \infty \right[ \left]4, \infty \right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c5d3a99841b133f88d73068672c0918d.png) .
.
- Pour
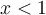 ; la fonction
; la fonction 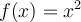 est polynômiale, elle est donc définie sur tout l'intervalle
est polynômiale, elle est donc définie sur tout l'intervalle ![\left]-\infty, 1\right[ \left]-\infty, 1\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3fe97ae4b91d11cc8f6bcd108273a994.png) .
. - Pour
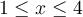 ; la fonction
; la fonction 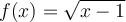 est définie si l'intérieur de la racine est positif ou nul. Or, on a que
est définie si l'intérieur de la racine est positif ou nul. Or, on a que 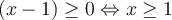 ,
,![\left[1, 4\right] \left[1, 4\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1ea2e67281c7305bfbfecbd88389a397.png) .
. - Pour
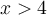 ; la fonction
; la fonction 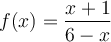 est définie si le dénominateur est non nul. Or, on a que
est définie si le dénominateur est non nul. Or, on a que 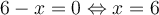 .
. est définie sur
est définie sur ![\left]4, 6\right[ \cup \left]6, \infty\right[ \left]4, 6\right[ \cup \left]6, \infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3e531d7c27cd66e1f0b8bbbcfa18137c.png) .
.
Par conséquent, en prenant l'union des domaines des trois parties, on obtient que :
Vous pouvez vous amuser à modifier les sous-intervalles de la fonction précédente dans le graphique Geogebra ci-dessous.
Dans ce graphique, la fonction  est définie par
est définie par
Ainsi, les trois sous-intervalles de définition sont : ![\left]-\infty, a_1\right[ \left]-\infty, a_1\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2e557138a058069d548c88cb8f0014ce.png) ,
, ![\left[a_1, a_2\right] \left[a_1, a_2\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c7450809725930c5a81109f544b622a1.png) et
et ![\left]a_2, \infty\right[ \left]a_2, \infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f8e19cc89deae188980f891618f4311f.png) .
.
![]() Déplacez le point bleu sur l'axe des
Déplacez le point bleu sur l'axe des  avec le pointeur. Son image
avec le pointeur. Son image 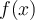 est calculée dans le rectangle bleu en utilisant l'équation de la courbe rose, c'est-à-dire la branche de la courbe associée au sous-intervalle possédant la valeur de
est calculée dans le rectangle bleu en utilisant l'équation de la courbe rose, c'est-à-dire la branche de la courbe associée au sous-intervalle possédant la valeur de  . Vous pouvez donc voir pour quelles valeurs de
. Vous pouvez donc voir pour quelles valeurs de  la fonction est définie. De plus, en déplaçant les curseurs associés aux paramètres
la fonction est définie. De plus, en déplaçant les curseurs associés aux paramètres 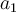 et
et 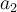 afin de modifier leurs valeurs, vous pouvez observer le changement sur le domaine de la fonction.
afin de modifier leurs valeurs, vous pouvez observer le changement sur le domaine de la fonction.
![]() Ex. : Modifiez
Ex. : Modifiez 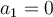 et
et 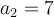 en déplaçant leur curseur. On a que
en déplaçant leur curseur. On a que ![\text{dom}f = \left]-\infty, 0\right[ \cup \left[1,\infty\right[ \text{dom}f = \left]-\infty, 0\right[ \cup \left[1,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c95980a831dc1145094151a4c2d3f858.png) . En déplaçant le point sur l'axe des
. En déplaçant le point sur l'axe des  sur l'intervalle
sur l'intervalle 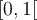 , vous pouvez voir que
, vous pouvez voir que 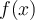 n'existe pas, donc que la fonction n'est pas définie sur cet intervalle.
n'existe pas, donc que la fonction n'est pas définie sur cet intervalle.
![v(t) = \left\{ {\begin{array}{cll} \frac{5}{3} t&\text{si}& 0 \leq t \leq 10 \\[0.8em] \frac{50}{3}&\text{si}&10 < t < 25 \\[0.8em] \frac{50}{3} -\frac{25}{6}\left({ t-25}\right)&\text{si}&25 \leq t \leq 29 \end{array}}\right. v(t) = \left\{ {\begin{array}{cll} \frac{5}{3} t&\text{si}& 0 \leq t \leq 10 \\[0.8em] \frac{50}{3}&\text{si}&10 < t < 25 \\[0.8em] \frac{50}{3} -\frac{25}{6}\left({ t-25}\right)&\text{si}&25 \leq t \leq 29 \end{array}}\right.](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c8a637b8576b8af9dede73689acd223d.png)
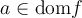
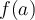

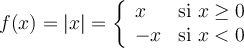
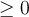
![f(x)=\left\{{\begin{array}{ll} x^2 & \text{si } x < 1 \\[0.8em] \sqrt{x-1} & \text{si } 1 \leq x \leq 4 \\[0.8em] \dfrac{x+1}{6-x} & \text{si } x > 4 \end{array}}\right. f(x)=\left\{{\begin{array}{ll} x^2 & \text{si } x < 1 \\[0.8em] \sqrt{x-1} & \text{si } 1 \leq x \leq 4 \\[0.8em] \dfrac{x+1}{6-x} & \text{si } x > 4 \end{array}}\right.](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0f6656fd7ae15aef0ea940bdaa6d9fa8.png)
![\text{dom}f = \left]-\infty, 6\right[ \cup \left]6, \infty\right[ \text{dom}f = \left]-\infty, 6\right[ \cup \left]6, \infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/832cb4561654d479dc50e179abed81c9.png)
![f(x)=\left\{{\begin{array}{ll} x^2 & \text{si } x < a_1 \\[0.8em] \sqrt{x-1} & \text{si } a_1 \leq x \leq a_2 \\[0.8em] \dfrac{x+1}{6-x} & \text{si } x > a_2 \end{array}}\right. f(x)=\left\{{\begin{array}{ll} x^2 & \text{si } x < a_1 \\[0.8em] \sqrt{x-1} & \text{si } a_1 \leq x \leq a_2 \\[0.8em] \dfrac{x+1}{6-x} & \text{si } x > a_2 \end{array}}\right.](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c0a1b786e34dbde8d00fd9d0b4fab391.png)