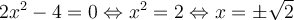2.5 Fonctions exponentielles et logarithmiques: Introduction

2.5 Fonctions exponentielles et logarithmiques

Introduction
Fonction exponentielle
Nombre d'Euler
Logarithme et ses propriétés
Table des logarithmes décimaux
Fonction logarithmique
Équations contenant des fonctions exponentielles et logarithmiques

1. Introduction

Nous connaissons bien la différence entre les nombres rationnels et irrationnels. Tous les nombres qui peuvent s'écrire sous la forme d'une fraction sont des nombres rationnels. Par exemple :

Nombre rationnel	Fraction correspondante
$2,5$	$\dfrac{5}{2}$
$0,125$	$\dfrac{1}{8}$
$0,\overline{3}$	$\dfrac{1}{3}$
$1,\overline{714285}$	$\dfrac{12}{7}$
$3,\overline{9}$	$\dfrac{4}{1}$

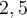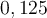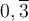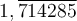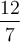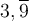Ainsi, un nombre qui possède un développement décimal fini ou périodique est un nombre rationnel, tandis qu'un nombre qui s'écrit à l'aide d'un nombre infini de décimales sans suite logique est un nombre irrationnel. Certains des nombres les plus célèbres sont des nombres irrationnels :

$\begin{array}{lcl} \pi & = & 3,141 \: 592 \: 653 \: 59... \\ e & = & 2,718 \: 281 \:828\: 46... \\ \sqrt{2} & = & 1, 414 \: 213\: 562\: 37... \end{array}$

Parmi les nombres irrationnels, on peut faire une distinction importante. Certains d'entre eux sont dits transcendants alors que d'autres sont algébriques. Voici un exemple pour bien comprendre la différence entre ces deux notions. Résolvons l'équation suivante :

$2x^2-4=0\Leftrightarrow x^2 = 2 \Leftrightarrow x=\pm \sqrt{2}$

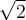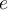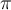Nous pouvons dire que le nombre $\sqrt{2}$ est un nombre algébrique, car il est solution d'une équation polynomiale à coefficients entiers. Un nombre est dit transcendant s'il n'est pas solution de ce type d'équation, par exemple les nombres $e$ et $\pi$ . La démonstration de la transcendance de ces nombres n'est pas de tout repos, mais pour les curieux, cliquez sur ce lien : Quelques démonstrations mathématiques simples. Vous y trouverez même quelques démonstrations d'irrationalité.