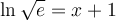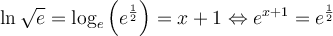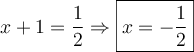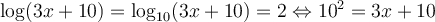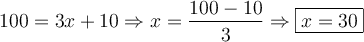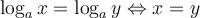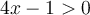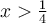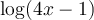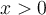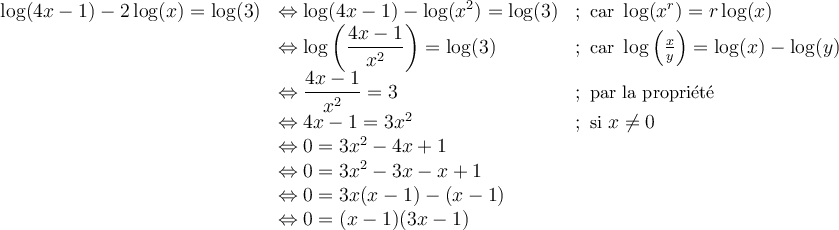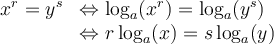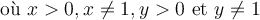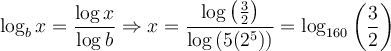2.5 Fonctions exponentielles et logarithmiques
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 2.5 Fonctions exponentielles et logarithmiques |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 06:47 |
Description
- Introduction
- Fonction exponentielle
- Nombre d'Euler
- Logarithme et ses propriétés
- Table des logarithmes décimaux
- Fonction logarithmique
- Équations contenant des fonctions exponentielles et logarithmiques
1. Introduction
Nous connaissons bien la différence entre les nombres rationnels et irrationnels. Tous les nombres qui peuvent s'écrire sous la forme d'une fraction sont des nombres rationnels. Par exemple :
| Nombre rationnel | Fraction correspondante |
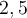 |
 |
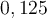 |
 |
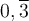 |
 |
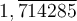 |
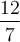 |
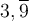 |
 |
Ainsi, un nombre qui possède un développement décimal fini ou périodique est un nombre rationnel, tandis qu'un nombre qui s'écrit à l'aide d'un nombre infini de décimales sans suite logique est un nombre irrationnel. Certains des nombres les plus célèbres sont des nombres irrationnels :
Parmi les nombres irrationnels, on peut faire une distinction importante. Certains d'entre eux sont dits transcendants alors que d'autres sont algébriques. Voici un exemple pour bien comprendre la différence entre ces deux notions. Résolvons l'équation suivante :
Nous pouvons dire que le nombre 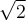 est un nombre algébrique, car il est solution d'une équation polynomiale à coefficients entiers. Un nombre est dit transcendant s'il n'est pas solution de ce type d'équation, par exemple les nombres
est un nombre algébrique, car il est solution d'une équation polynomiale à coefficients entiers. Un nombre est dit transcendant s'il n'est pas solution de ce type d'équation, par exemple les nombres  et
et 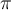 . La démonstration de la transcendance de ces nombres n'est pas de tout repos, mais pour les curieux, cliquez sur ce lien : Quelques démonstrations mathématiques simples. Vous y trouverez même quelques démonstrations d'irrationalité.
. La démonstration de la transcendance de ces nombres n'est pas de tout repos, mais pour les curieux, cliquez sur ce lien : Quelques démonstrations mathématiques simples. Vous y trouverez même quelques démonstrations d'irrationalité.
2. Fonction exponentielle
Les fonctions exponentielles peuvent décrire plusieurs phénomènes importants en mathématiques appliquées et sont notamment utilisées pour prévoir la taille d'une population, pour déterminer l'âge d'un objet ancien en archéologie, pour calculer la valeur d'une hypothèque, etc.
Qu'ont en commun ces phénomènes et pourquoi peuvent-ils être décrits selon un modèle exponentiel? Considérons la situation suivante :
Supposons qu'un troupeau d'éléphants double à tous les 6 ans. Si le troupeau compte 7 éléphants en 2010,
en 2016 (6 ans plus tard) la population du troupeau sera de 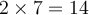 éléphants (elle aura doublé),
éléphants (elle aura doublé),
en 2022, la population du troupeau sera de 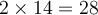 éléphants ou bien
éléphants ou bien 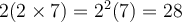 ,
,
en 2028, la population du troupeau sera de 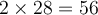 éléphants ou bien
éléphants ou bien 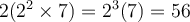 ,
,
...
après  période(s) de 6 années, la population du troupeau sera de
période(s) de 6 années, la population du troupeau sera de 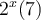 éléphants.
éléphants.
La variable  représente le temps et elle est l'exposant dans l'expression ci-dessus. Par conséquent, on dira que la population du troupeau d'éléphants varie en fonction du temps et selon un modèle exponentiel.
représente le temps et elle est l'exposant dans l'expression ci-dessus. Par conséquent, on dira que la population du troupeau d'éléphants varie en fonction du temps et selon un modèle exponentiel.
La population 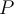 d'éléphants varie donc en fonction du temps
d'éléphants varie donc en fonction du temps  par un modèle exponentiel décrit par l'équation
par un modèle exponentiel décrit par l'équation 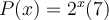 .
.
De façon générale,
Pour bien comprendre la fonction exponentielle et ses caractéristiques principales, il faut savoir manipuler adéquatement les propriétés des exposants entiers et rationnels. Dans cette section, nous faisons un rappel de ces propriétés, mais voici celles qui vous seront d'une grande utilité :
Par ces lois, on peut donner une explication logique à l'expression 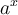 , où
, où 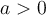 .
.
- Si l'exposant est un entier positif
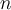 , alors
, alors 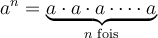 ;
; - Si l'exposant est un entier négatif
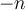 , alors
, alors 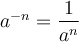 ;
; - Si l'exposant est un nombre rationnel
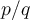 , où
, où 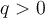 , alors
, alors ![a^{p/q}=\sqrt[q]{a^p}=\left({\sqrt[q]{a}}\right)^p a^{p/q}=\sqrt[q]{a^p}=\left({\sqrt[q]{a}}\right)^p](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9ebc8192f407efb646a4d8fbaf0c19f8.png) .
.
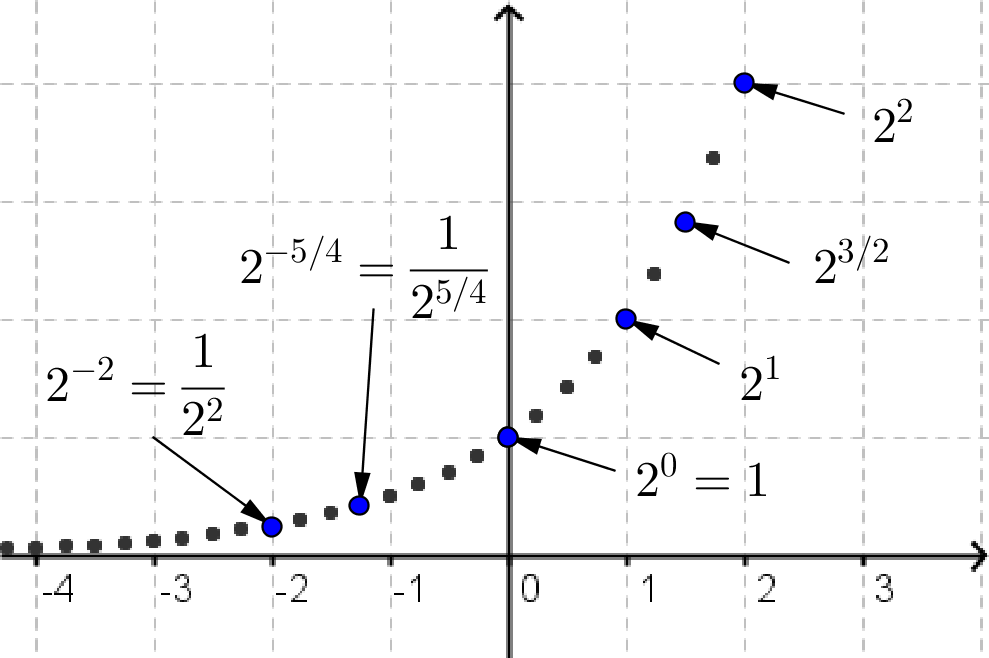
Cependant, si l'exposant est un nombre irrationnel, quelle explication peut-on donner ? Analysons plus en détails la fonction 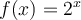 afin de répondre à cette question. Dans la figure ci-dessus, les trous dans le graphique sont en fait les valeurs de
afin de répondre à cette question. Dans la figure ci-dessus, les trous dans le graphique sont en fait les valeurs de 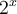 lorsque
lorsque  est un nombre irrationnel. Ainsi, ces valeurs sont comprises entre deux autres valeurs de
est un nombre irrationnel. Ainsi, ces valeurs sont comprises entre deux autres valeurs de 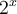 possédant des exposants rationnels.
possédant des exposants rationnels.
Par exemple, cherchons la valeur du nombre 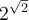 . On sait que
. On sait que
alors
Nous aurons de meilleures approximations de 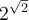 si nous prenons des valeurs rationnelles de
si nous prenons des valeurs rationnelles de  de plus en plus près de
de plus en plus près de 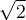 .
.
Représentations des fonctions exponentielles
Il existe deux types de fonctions exponentielles 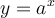 , celles dont
, celles dont 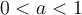 et celles dont
et celles dont 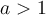 . À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions exponentielles pour différentes valeurs positives de
. À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions exponentielles pour différentes valeurs positives de 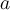 .
.
Toutes ces fonctions ont comme point commun 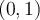 , car si l'exposant est
, car si l'exposant est 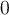 , alors
, alors
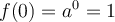
pour toute valeur positive de 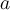 .
.
- Si
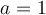 , la fonction obtenue est la droite horizontale
, la fonction obtenue est la droite horizontale 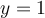 , car
, car 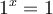 quelle que soit la valeur de l'exposant réel.
quelle que soit la valeur de l'exposant réel.
![]() Déplacez le curseur vertical à droite afin de remarquer l'effet obtenu sur le graphique en augmentant ou en diminuant la valeur de la base
Déplacez le curseur vertical à droite afin de remarquer l'effet obtenu sur le graphique en augmentant ou en diminuant la valeur de la base 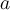 .
.
- Si
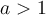 (au dessus de la ligne rose)
(au dessus de la ligne rose) - La fonction est croissante sur le domaine
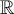 .
. - Les valeurs de
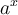 sont strictement positives, ainsi l'image est
sont strictement positives, ainsi l'image est![\left]{0, \infty}\right[ \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d13a6e4c304d2f4a427dad83ef19750a.png) . Cela signifie que la fonction possède l'axe des
. Cela signifie que la fonction possède l'axe des  comme asymptote horizontale.
comme asymptote horizontale. - Si
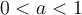
- On peut remarquer qu'étant donné que
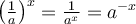 , le graphique de
, le graphique de 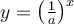 est une réflexion du graphique de
est une réflexion du graphique de 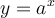 par rapport à l'axe des
par rapport à l'axe des 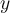 (voir la section : Transformations de fonctions).
(voir la section : Transformations de fonctions). - La fonction est décroissante sur le domaine
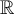 .
. - Son image est
![\left]{0,\infty}\right[ \left]{0,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6dd307f673b8f1b9fa5cdb6b6c78a955.png) .
.
Faites apparaître la fonction exponentielle 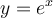
![]() en cochant la case associée. La courbe représentant cette fonction est en vert. Cette fonction possède des propriétés bien spéciales que nous explorons dans la section suivante.
en cochant la case associée. La courbe représentant cette fonction est en vert. Cette fonction possède des propriétés bien spéciales que nous explorons dans la section suivante.
![]() Pour l'instant, en déplaçant le curseur vertical pour déplacer la courbe rouge de plus en plus près de la courbe verte, vous obtenez une petite approximation de la valeur de cette base
Pour l'instant, en déplaçant le curseur vertical pour déplacer la courbe rouge de plus en plus près de la courbe verte, vous obtenez une petite approximation de la valeur de cette base  .
.
Vous remarquez que la valeur de  est très proche de
est très proche de 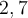 . En fait, ce nombre est irrationnel, donc son développement décimal n'est pas périodique. On l'appelle le nombre d'Euler et sa valeur approximative est :
. En fait, ce nombre est irrationnel, donc son développement décimal n'est pas périodique. On l'appelle le nombre d'Euler et sa valeur approximative est :
Exercices formatifs WeBWorK
 Fonction exponentielle
Fonction exponentielle
3. Nombre d'Euler
Les applications du nombre  sont variées. Au moyen de la fonction exponentielle, il est utilisé en économie (calcul des intérêts versés de façon continue), en biologie (mesure de la multiplication des cellules vivant dans un organisme), en sciences physiques, etc.
sont variées. Au moyen de la fonction exponentielle, il est utilisé en économie (calcul des intérêts versés de façon continue), en biologie (mesure de la multiplication des cellules vivant dans un organisme), en sciences physiques, etc.
C'est le mathématicien Leonhard Euler qui, en 1727, a choisi la lettre  pour désigner cette constante. Même s'il s'agit de l'initiale de son nom, ce serait plutôt parce que e est la première lettre du mot exponentiel. Euler obtient une estimation de
pour désigner cette constante. Même s'il s'agit de l'initiale de son nom, ce serait plutôt parce que e est la première lettre du mot exponentiel. Euler obtient une estimation de  avec 18 décimales en utilisant la formule suivante :
avec 18 décimales en utilisant la formule suivante :
Si vous n'avez jamais vu le symbole « ! », il signifie factoriel, par exemple 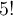 se dit « 5 factoriel » et est égal à
se dit « 5 factoriel » et est égal à 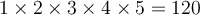 .
.
Mais bien avant les études d'Euler sur le nombre  , ce nombre fabuleux fit sa première apparition en 1618, dans un livre de John Napier, qui traitait des logarithmes. Eh oui, les logarithmes étaient pour les mathématiciens et scientifiques de cette époque bien plus intéressants à étudier, car ils facilitaient les calculs astronomiques qu'ils devaient faire. C'est pourquoi
, ce nombre fabuleux fit sa première apparition en 1618, dans un livre de John Napier, qui traitait des logarithmes. Eh oui, les logarithmes étaient pour les mathématiciens et scientifiques de cette époque bien plus intéressants à étudier, car ils facilitaient les calculs astronomiques qu'ils devaient faire. C'est pourquoi  n'était pas en lui-même le centre d'intérêt. Ce livre définissait
n'était pas en lui-même le centre d'intérêt. Ce livre définissait  comme la base du logarithmique naturel qui, dans le langage d'aujourd'hui, est défini de la façon suivante :
comme la base du logarithmique naturel qui, dans le langage d'aujourd'hui, est défini de la façon suivante :
À cette époque, on ne remarqua par les merveilleuses possibilités du nombre  . Ce n'est que plusieurs années plus tard, précisément en 1683, que Jacob Bernoulli, un mathématicien qui s'intéressait à la finance et aux intérêts composés, donna une première estimation de
. Ce n'est que plusieurs années plus tard, précisément en 1683, que Jacob Bernoulli, un mathématicien qui s'intéressait à la finance et aux intérêts composés, donna une première estimation de  à l'aide du concept de limite (cette notion est abordée dans le cours Calcul différentiel).
à l'aide du concept de limite (cette notion est abordée dans le cours Calcul différentiel).
L'activité suivante vous permettra de comprendre cette estimation.
Un placement d'argent à la banque engendre des intérêts composés lorsque, à la fin de chaque période, les intérêts sont ajoutés au placement afin de générer de nouveaux intérêts.
Même si ce n'est pas représentatif de la réalité, si l'on investit une somme de 1 $ à un taux d'intérêt annuel de 100 % et si les intérêts sont calculés une fois par année, la valeur de ce placement à la fin de l'année est de :
1 $ × 2 = 2 $
Vous avez fait 1 $ d'intérêt sur votre 1 $ de placement.
Mais si les intérêts annuels de 100 % sont calculées 2 fois par année (aux 6 mois), la valeur du placement à la fin de l'année se calcule ainsi :
- après 6 mois : 1 $ + 1 × 50 % = 1 + 0,5 = 1,50 $
- après 12 mois : 1,50 $ + 1,50 × 50 % = 1,50 (1 + 0,5) = 1,50 × 1,5 = 2,25 $
Au total, la somme accumulée sera de 1 $ × 1,5 × 1,5 = 2,25 $
Complétez maintenant le tableau suivant :
Vous pouvez comparer vos réponses avec l'application Geogebra suivante :
Elle évalue l'expression de la dernière ligne pour différentes valeurs de n. ![]() Déplacez le curseur n afin de faire augmenter sa valeur ou, tout simplement, entrez la valeur de n désirée dans le champ de saisie. De quelle valeur l'expression
Déplacez le curseur n afin de faire augmenter sa valeur ou, tout simplement, entrez la valeur de n désirée dans le champ de saisie. De quelle valeur l'expression 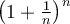 se rapproche-t-elle lorsque la valeur de n est de plus en plus grande ?
se rapproche-t-elle lorsque la valeur de n est de plus en plus grande ?
La réponse est le nombre d'Euler 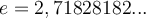
En effet, si l'on investit une somme de 1 $ à un taux d'intérêt annuel de 100 % et que les intérêts sont calculés de façon continue, cela signifie que n prend des valeurs infiniment grandes, ainsi la valeur de notre placement à la fin de l'année sera :
Pour terminer, voici un extrait du « Théorème du perroquet », un roman de Denis Guedj publié en 1998 et qui illustre bien cette dernière représentation du nombre  :
:
Si au lieu de toucher les intérêts à la fin de l'année, tu les avais touchés tous les six mois et que tu les aies replacés, au bout d'un an ça t'aurait fait P(1 + 1/2)2. Calcule ! Tu aurais plus que doublé ton pécule tu aurais 2,25P. Si au lieu de toucher les intérêts tous les six mois, tu les avais touchés tous les trimestres et que tu les aies replacés, au bout de l'année, ça t'aurait fait P(1 + 1/4)4. Calcule ! Tu aurais gagné encore plus : 2,441P. Si tu les avais touchés tous les mois et que tu les aies replacés, ça t'aurait fait P(l + 1/12)12. Calcule ! 2, 596. Encore plus ! Puis, tous les jours : P(1 + 1/365)365. Encore plus toutes les secondes, encore plus. Et puis, tous les riens du tout, « en continu ». Tu n'en peux plus, tu t'envoles, tu planes, tu te dis que c'est Byzance, que ton pécule pécuple, qu'il va quadrupler, décupler, centupler, millionupler, milliardupler, [ ... ] Tes intérêts composés, ils ont beau se décomposer, eh bien, à l'arrivée, tu n'as même pas le triple de ton pécule, ni même 2,9 fois plus, ni même 2,8 fois plus, ni même 2,75 fois plus, ni même 2,72 fois plus... Tu as seulement 2, 71 828 1828 ! ... Mon pauvre John, après toute cette richesse, te voilà seulement e fois moins pauvre qu'au départ ! »
4. Logarithme et ses propriétés
Les origines du logarithme

John Napier
Au XVIe siècle, les calculatrices n'existaient évidemment pas encore et les nombres décimaux n'étaient pas d'usage courant. Pourtant, l'astronomie, la navigation et le commerce demandaient d'effectuer des opérations de plus en plus complexes avec des nombres très élevés. C'est ainsi que le mathématicien John Napier, aussi connu sous le nom francisé de Neper, publie en 1614 un outil permettant de simplifier les calculs opératoires : le logarithme.
Au départ, Neper a développé les logarithmes pour simplifier les calculs de trigonométrie utiles en astronomie. Il donne ainsi une première table des logarithmes des sinus d'angles. L'astronome écossais Jost Bürgi aurait également inventé les logarithmes au même moment et indépendamment, mais sa publication est postérieure.
Toutefois, les logarithmes ne trouveront leur essor dans la communauté scientifique qu'après la mort de Napier. Le mathématicien anglais Henry Briggs (1561-1630) imagina un autre système de logarithmes en base 10, aussi appelés logarithmes vulgaires ou décimaux, qui seront rapidement adoptées par tous.
Pour comprendre comment fonctionnait ces calculs, il faut d'abord définir les logarithmes.Commençons avec le logarithme en base 10. On décida de définir les logarithmes décimaux, noté 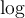 , comme les exposants de 10. Ainsi,
, comme les exposants de 10. Ainsi,
Par exemple,
On comprend bien cette définition avec des puissances positives et négatives de 10, mais 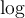 ne donne pas nécessairement une valeur entière. Par exemple,
ne donne pas nécessairement une valeur entière. Par exemple,
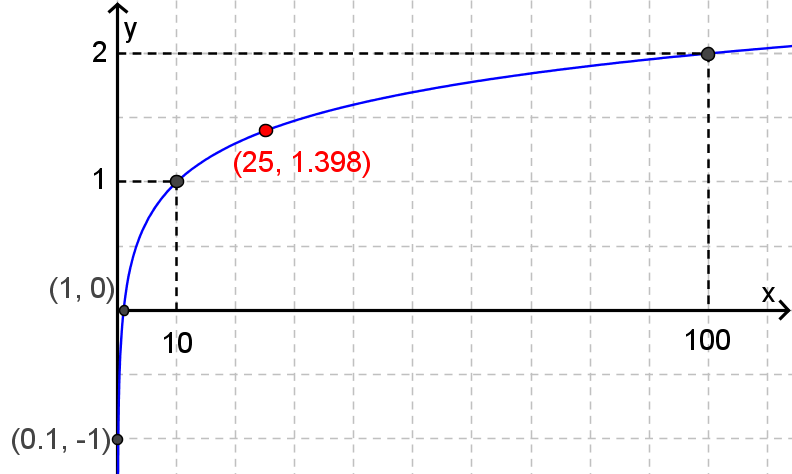
Si log(10) = 1 et log(100) = 2, alors on imagine que pour tout nombre  situé entre 10 et 100, log(x) est situé entre 1 et 2. En effet, log(25) = 1,397...
situé entre 10 et 100, log(x) est situé entre 1 et 2. En effet, log(25) = 1,397...
Ainsi, log est une fonction qui associe une valeur log(x) (l'exposant de 10) à chaque valeur de  donnée. On peut construire la courbe représentative de la fonction logarithmique de base 10 pour les valeurs de
donnée. On peut construire la courbe représentative de la fonction logarithmique de base 10 pour les valeurs de  strictement positives.
strictement positives.
Propriétés des logarithmes
L'idée de départ de l'utilisation des logarithmes était de remplacer les multiplications par des additions et les divisions par des soustractions afin de faciliter, rappelons-le, les calculs astronomiques à une époque où tout se faisait manuellement. Observons le tableau suivant.

La dernière ligne représente ce qu'on appelle une progression géométrique de raison 10 (101, 102, 103, 104) et la première ligne représente plutôt une progression arithmétique de raison 1 (1, 2, 3, 4). Tout simplement, lorsqu'on multiplie des puissances de 10 ensemble, il existe un lien d'addition entre leurs exposants. C'est ce que représente la propriété des exposants suivante :
Par exemple, on sait que log(10)=1, log(102)=2 et log(103)=3. On peut donc écrire
De plus, on sait que 103 = 10 × 102. Alors on peut conclure que
On peut généraliser cette propriété pour tout nombre réel positif et on peut également en déduire une propriété équivalente pour les soustractions de log.
On peut aussi déduire d'autres propriétés tout aussi importantes à partir de ces dernières.
Voici quelques exemples d'applications des propriétés précédentes.
Exercices formatifs WeBWorK
 Propriétés des logarithmes
Propriétés des logarithmes
5. Table des logarithmes décimaux
Avant l'arrivée des calculatrices et des ordinateurs, il n'y a pas si longtemps d'ailleurs, on utilisait des tables de logarithmes pour faire des calculs périlleux comportant des multiplications, des divisions et des exposants.
Tout d'abord, étant donné que nous travaillons avec les logarithmes décimaux, on peut remarquer la caractéristique suivante :
 |
 |
|
| 100 = 1 | 2 | 0,30103 |
| 5 | 0,69897 | |
| 101 | 12 | 1,07918 |
| 75 | 1,87506 | |
| 102 | 225 | 2,35218 |
| 600 | 2,77815 | |
| 835 | 2,92168 | |
| 103 | 1200 | 3,07918 |
| 5310 | 3,72509 | |
| 9420 | 3,97405 |
Par la propriété des logarithmes, si on prend par exemple le nombre 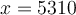 , on aura
, on aura
Par conséquent, dans une table, le logarithme d'un nombre se compose de deux parties :
- Une partie entière (3) qui indique l'ordre de grandeur du nombre
 : c'est la caractéristique. C'est aussi l'exposant de la puissance de 10 la plus près et inférieure à notre nombre.
: c'est la caractéristique. C'est aussi l'exposant de la puissance de 10 la plus près et inférieure à notre nombre. - Une partie décimale (0,72509), qui porte le nom de mantisse. C'est cette dernière qui est lue sur la table.
Par exemple, comme 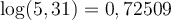 , on peut déduire les logarithmes de 531 et 53100.
, on peut déduire les logarithmes de 531 et 53100.
a) Calculons le produit suivant :
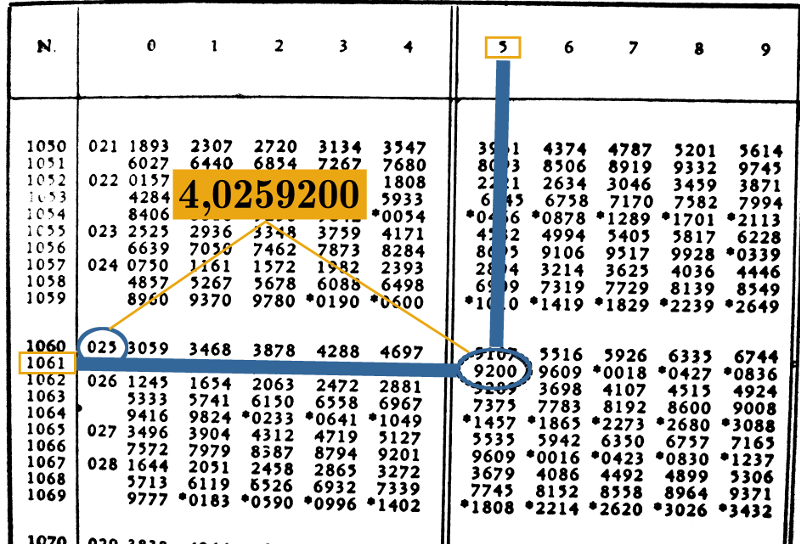
En lisant sur une table de logarithmes, on trouve que
On peut ainsi conclure que
b) Donnons une approximation du nombre
À la calculatrice, ce calcul est impossible, mais en utilisant les propriétés des logarithmes, on peut approximer ce nombre. En effet,
Pour trouver notre nombre, on va avoir besoin de trouver le nombre dont le logarithme correspond à 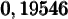 . En lisant sur une table de logarithme, on trouve que
. En lisant sur une table de logarithme, on trouve que
On peut donc conclure que
et donc
6. Fonction logarithmique
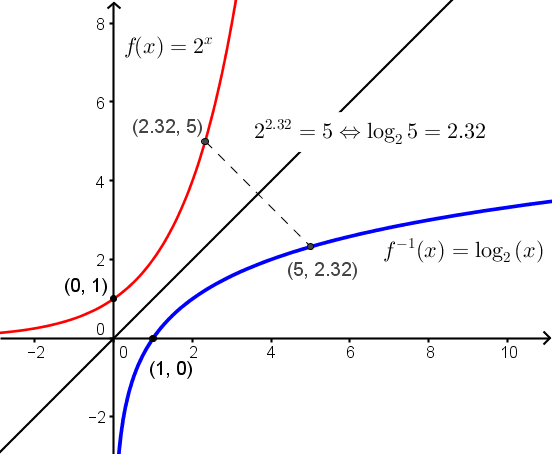
La fonction logarithmique est la fonction réciproque de la fonction exponentielle. Si 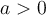 et
et 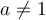 , la fonction exponentielle
, la fonction exponentielle 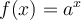 possède une fonction réciproque
possède une fonction réciproque 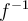 , qu'on appelle la fonction logarithmique de base
, qu'on appelle la fonction logarithmique de base 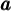 et que l'on note
et que l'on note 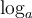 .
.
Par définition de la fonction réciproque, le graphique de la fonction logarithmique est la réflexion des points du graphique de la fonction exponentielle par rapport à la droite 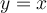 . Par conséquent, on aura :
. Par conséquent, on aura :
De plus, sachant que deux fonctions réciproques sont telles que 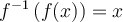 et
et 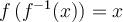 , on peut déduire deux autres propriétés des logarithmiques.
, on peut déduire deux autres propriétés des logarithmiques.
Ces deux dernières propriétés nous permettent de créer la formule de changement de base suivante :
Preuve :
La formule de changement de base est utile pour calculer, à l'aide de la calculatrice, des valeurs comme 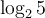 en utilisant le logarithme décimal
en utilisant le logarithme décimal 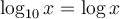 ou le logarithme naturel
ou le logarithme naturel 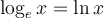 . En effet,
. En effet,
Représentations des fonctions logarithmiques
Il existe deux types de fonctions logarithmiques 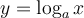 , celles pour lesquelles
, celles pour lesquelles 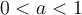 et celles pour lesquelles
et celles pour lesquelles 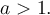 À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions logarithmiques pour ces différentes valeurs positives de
À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions logarithmiques pour ces différentes valeurs positives de 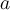 .
.
Toutes ces fonctions ont comme point commun 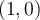 , car si l'exposant est
, car si l'exposant est 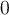 , alors
, alors
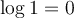 , car
, car 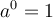
pour toutes valeurs positives de 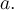
De plus, ![\text{dom }f = \left]{0, \infty}\right[ \text{dom }f = \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3002e546d7172a9563ec19bf9dd43cfc.png) . Cela signifie que la fonction possède une asymptote verticale, soit l'axe des
. Cela signifie que la fonction possède une asymptote verticale, soit l'axe des 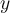 . Finalement, il n'y a ni minimum, ni maximum, de sorte que l'image de la fonction est
. Finalement, il n'y a ni minimum, ni maximum, de sorte que l'image de la fonction est 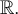
![]() Déplacez le curseur vertical à droite afin de noter l'effet sur le graphique de l'augmentation et de la diminution de la base
Déplacez le curseur vertical à droite afin de noter l'effet sur le graphique de l'augmentation et de la diminution de la base 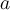 .
.
Fonction logarithmique naturel 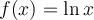
![]() Faites apparaître la fonction logarithmique
Faites apparaître la fonction logarithmique 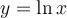 en cochant la case associée. La courbe représentant cette fonction est en vert. En déplaçant le curseur vertical pour que la courbe rouge se rapproche de plus en plus de la courbe verte, vous remarquez que la base
en cochant la case associée. La courbe représentant cette fonction est en vert. En déplaçant le curseur vertical pour que la courbe rouge se rapproche de plus en plus de la courbe verte, vous remarquez que la base 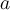 s'approche du nombre d'Euler
s'approche du nombre d'Euler 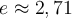 . Le logarithme naturel est en fait le logarithmique de base
. Le logarithme naturel est en fait le logarithmique de base  .
.
Ainsi, la fonction 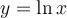 est la fonction réciproque de la fonction exponentielle
est la fonction réciproque de la fonction exponentielle 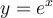 . On peut en déduire que
. On peut en déduire que
Le domaine de fonctions logarithmiques composées
Dans une section précédente, nous avons vu les conditions à respecter pour trouver le domaine d'une fonction composée. Cliquez sur ce lien si vous désirez vous rafraîchir la mémoire. Pour trouver le domaine d'une fonction composée, il faut tenir compte du domaine de chacune des fonctions qui la compose. Voici un exemple où la fonction logarithmique fait partie d'une de ces fonctions.
Trouvons le domaine de la fonction 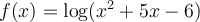 .
.
solution Puisque la fonction 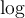 est définie seulement sur les réels positifs, c'est-à-dire sur
est définie seulement sur les réels positifs, c'est-à-dire sur ![\left]0,+\infty\right[ \left]0,+\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8a44a3d914a6c2134c9bda0c382a20dd.png) , il faut que la fonction « à l'intérieur » du
, il faut que la fonction « à l'intérieur » du 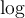 appartienne à cet intervalle.
appartienne à cet intervalle.
On peut exprimer notre fonction composée par  où
où 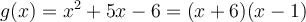 .
.
Ainsi, il faut trouver les valeurs de  pour que
pour que ![g(x)=(x+6)(x-1)\in\left]0,+\infty\right[ g(x)=(x+6)(x-1)\in\left]0,+\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/35e0e14a93be7832f85a539be77abf19.png) . Il faut donc résoudre l'inéquation
. Il faut donc résoudre l'inéquation
À partir du graphique de la fonction quadratique, on a que 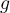 est strictement positive si
est strictement positive si  et
et 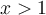 .
.
De plus, comme 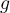 est définie sur les réels, on a que le domaine de
est définie sur les réels, on a que le domaine de 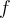 est
est ![\left]-\infty,-6\right[\cup\left]1,+\infty\right[ \left]-\infty,-6\right[\cup\left]1,+\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3d5fab69bf73cd6fc7755a12066f239c.png) .
.
Exercices formatifs WeBWorK
 Fonction logarithmique
Fonction logarithmique
 Autres propriétés des logarithmes
Autres propriétés des logarithmes
7. Équations contenant des fonctions exponentielles et logarithmiques
Dans une équation exponentielle, la variable qui se retrouve en exposant ne peut pas être isolée à l'aide des opérations arithmétiques de base 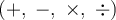 . De même, lorsqu'une équation comporte un ou plusieurs logarithmes, il faut d'abord effectuer une transformation pour faire disparaître ce dernier. Voici différentes catégories d'équations contenant des expressions exponentielles ou des logarithmes qui seront résolues dans cette page.
. De même, lorsqu'une équation comporte un ou plusieurs logarithmes, il faut d'abord effectuer une transformation pour faire disparaître ce dernier. Voici différentes catégories d'équations contenant des expressions exponentielles ou des logarithmes qui seront résolues dans cette page.
Nous aurons besoin des différentes propriétés des logarithmes vues dans les sections précédentes. Voici un tableau résumant ces propriétés.
Les équations contenant des expressions exponentielles qu'on peut ramener à une base commune
La propriété suivante dit que pour deux fonctions exponentielles égales, si les bases sont identiques, alors les exposants doivent être égaux.
Nous allons résoudre les équations suivantes à l'aide de cette propriété.
solution On peut exprimer 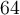 comme une puissance de
comme une puissance de 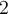 , ainsi :
, ainsi :

Les solutions de cette équation sont  et
et  .
.
solution Résoudre cette équation signifie isoler le  situé dans les exposants. Tout d'abord, il faut transformer les deux membres de l'égalité pour les mettre sur une base commune, soit
situé dans les exposants. Tout d'abord, il faut transformer les deux membres de l'égalité pour les mettre sur une base commune, soit 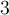 .
.
Les équations contenant des logarithmes
Nous avons vu qu'un logarithme n'est rien d'autre qu'un exposant. La définition de logarithme permet ainsi de transformer l'équation logarithmique en une équation exponentielle.
Cette égalité se traduit par la phrase suivante : « 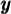 , le logarithme, est l'exposant que l'on doit attribuer à
, le logarithme, est l'exposant que l'on doit attribuer à 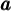 pour obtenir
pour obtenir 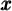 ».
».
Nous allons résoudre les équations suivantes à l'aide de cette définition.
solution On sait que
solution On sait que
Si les deux membres de l'égalité contiennent des logarithmes de même base, on peut utiliser la propriété de la fonction logarithmique suivante :
Nous allons résoudre l'équation 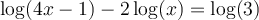 à l'aide de cette propriété.
à l'aide de cette propriété.
solution La solution de cette équation doit faire partie du domaine de l'équation, donc respecter les conditions suivantes :
Le domaine de l'équation est dont ![\left]\frac{1}{4},\infty\right[ \left]\frac{1}{4},\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7df16ac6a553c11ab9a673147f03a467.png) et la solution doit faire partie de ce domaine.
et la solution doit faire partie de ce domaine.
On résout l'équation de la façon suivante :
Les solutions de cette équation sont  et
et 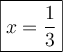 , car elles font parties du domaine.
, car elles font parties du domaine.
Les équations exponentielles que l'on peut résoudre à l'aide des logarithmes
Si l'on veut résoudre une équation contenant des exponentielles où il est impossible de trouver une base commune, il faut utiliser la propriété suivante :Nous allons résoudre l'équation 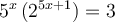 .
.
solution On ne peut pas trouver de base commune à 5 et 2. On utilise donc la propriété précédente en calculant le logarithme décimal à chaque membre de l'égalité.
La solution de l'équation est 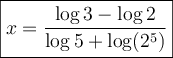 ou, en simplifiant à l'aide des propriétés des logarithmes,
ou, en simplifiant à l'aide des propriétés des logarithmes, 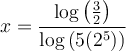 .
.
Pour le plaisir, on pourrait également exprimer cette solution à l'aide d'un seul logarithme en utilisant la formule de changement de base et le fait que 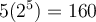 .
.

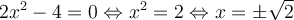
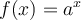
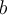
![\begin{array}{l@{ \hskip 5em}l} a^{x+y}=a^x a^y & a^{x-y}=\dfrac{a^x}{a^y} \\[0.8em] a^{xy}=\left({a^x}\right)^y & a^x b^x = \left({ab}\right)^x \end{array} \begin{array}{l@{ \hskip 5em}l} a^{x+y}=a^x a^y & a^{x-y}=\dfrac{a^x}{a^y} \\[0.8em] a^{xy}=\left({a^x}\right)^y & a^x b^x = \left({ab}\right)^x \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e4e8cb9218fd01ee954f1723be58274d.png)
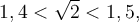
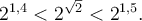
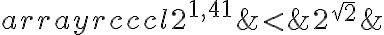
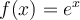
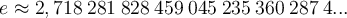
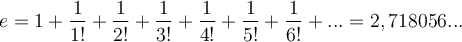
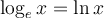
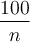
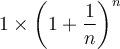
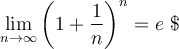
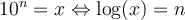

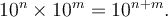
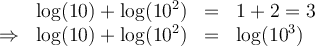
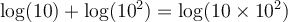
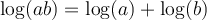
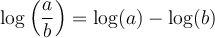
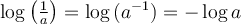
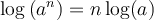
![\log\left({\sqrt[n]{a}}\right)=\dfrac{1}{n}\log(a) \log\left({\sqrt[n]{a}}\right)=\dfrac{1}{n}\log(a)](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2b0a33480737704c262c9df58e21cff0.png)
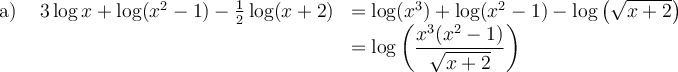
![\begin{array}{lrlr}\text{b) }&\dfrac{\log 5}{\log 100}+\log 1 &= \dfrac{\log 5}{\log_{10}(10^2)}+\log_{10}(10^0)&;\small\text{ attention: } \frac{\log a}{\log b}\neq\log a-\log b \\[0.8em]&&= \dfrac{\log 5}{2} + 0&\\[0.8em] &&=\frac{1}{2}(\log 5)&\\[0.8em]&&=\log\sqrt{5}&\end{array} \begin{array}{lrlr}\text{b) }&\dfrac{\log 5}{\log 100}+\log 1 &= \dfrac{\log 5}{\log_{10}(10^2)}+\log_{10}(10^0)&;\small\text{ attention: } \frac{\log a}{\log b}\neq\log a-\log b \\[0.8em]&&= \dfrac{\log 5}{2} + 0&\\[0.8em] &&=\frac{1}{2}(\log 5)&\\[0.8em]&&=\log\sqrt{5}&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/aa70f475b624d0bc12826d7497e0f1e5.png)
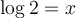
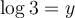
![\begin{array}{lrl}\text{a) }&\log\dfrac{8}{9}&=\log 8-\log 9\\[0.8em]&&=\log 2^3-\log 3^2\\[0.8em]&&=3\log 2 - 2\log 3\\[0.8em]&&=3x-2y \end{array} \begin{array}{lrl}\text{a) }&\log\dfrac{8}{9}&=\log 8-\log 9\\[0.8em]&&=\log 2^3-\log 3^2\\[0.8em]&&=3\log 2 - 2\log 3\\[0.8em]&&=3x-2y \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d5277db2aeb0f8c90362287e5fd1596a.png)
![\begin{array}{lrlr}\text{b) }&\log\sqrt{120}&=\dfrac{1}{2}\log(4\times 3\times 10)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 4 + \log 3 + \log 10\right)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 2^2 +\log 3 + 1\right)&;\small\text{ car } \log_{10} 10 = 1\\[0.8em]&&=\dfrac{1}{2}\left(2\log 2+\log 3 + 1\right)&\\[0.8em]&&=\dfrac{1}{2}\left(2x+y+1\right)& \end{array} \begin{array}{lrlr}\text{b) }&\log\sqrt{120}&=\dfrac{1}{2}\log(4\times 3\times 10)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 4 + \log 3 + \log 10\right)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 2^2 +\log 3 + 1\right)&;\small\text{ car } \log_{10} 10 = 1\\[0.8em]&&=\dfrac{1}{2}\left(2\log 2+\log 3 + 1\right)&\\[0.8em]&&=\dfrac{1}{2}\left(2x+y+1\right)& \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/207262676be5906b140d4faeb60dc95b.png)
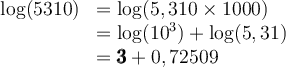
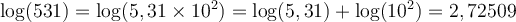
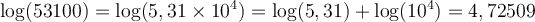
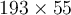
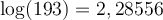
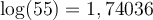
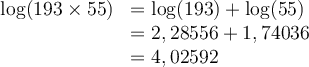
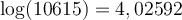
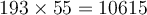
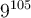
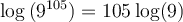
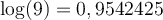
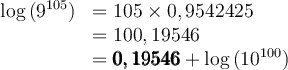
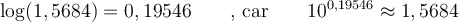
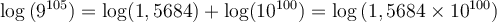
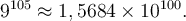
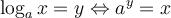
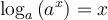
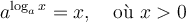
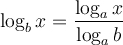
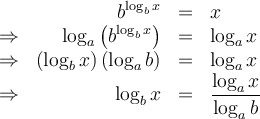
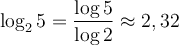
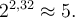
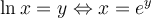
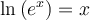
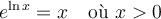
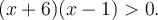
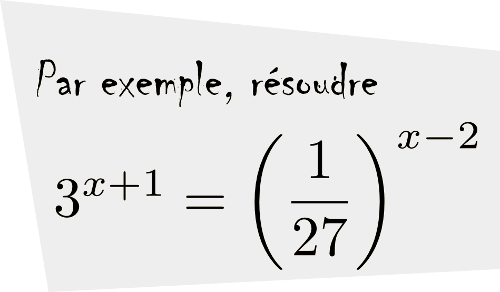
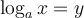
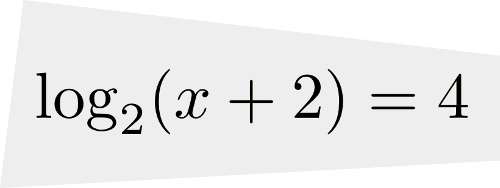
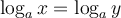
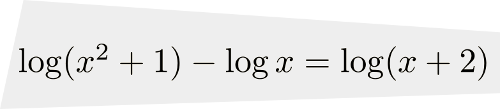
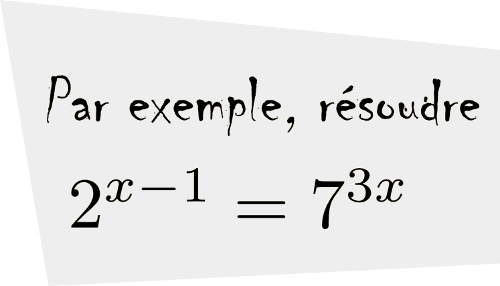
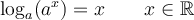
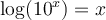
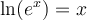
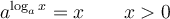
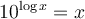
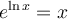
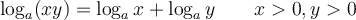
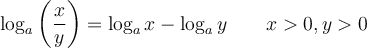
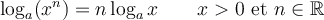
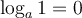
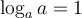
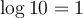
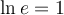
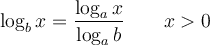
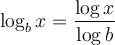
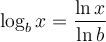
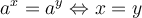
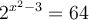
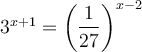
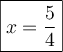
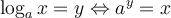
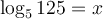
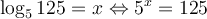
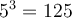
 b) Résoudre l'équation
b) Résoudre l'équation