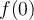2.1 Les fonctions
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 2.1 Les fonctions |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 04:51 |
Description
- Relation et fonction
- Domaine et image
- Graphique d'une fonction
- Points d'intersection avec les axes
1. Relation et fonction
En mathématiques, on définit une relation lorsque les éléments d'un ensemble de départ 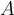 et d'un ensemble d'arrivée
et d'un ensemble d'arrivée 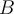 sont reliés par une loi quelconque
sont reliés par une loi quelconque 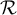 .
.
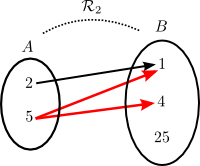
Exemple : Soit l'ensemble de départ 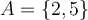 et l'ensemble d'arrivée
et l'ensemble d'arrivée 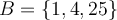 et les relations
et les relations
Ces relations peuvent être représentées par les diagrammes suivants :
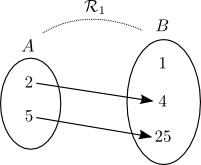
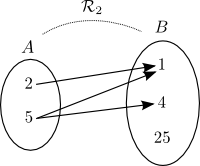
Chacune des relations est donc égale à l'ensemble des couples qui ont été formés entre les éléments des deux ensembles.
En fait, si on crée un ensemble contenant tous les couples 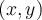 formés en prenant la première composante
formés en prenant la première composante  dans l'ensemble de départ
dans l'ensemble de départ 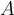 et la deuxième composante
et la deuxième composante  dans l'ensemble d'arrivée
dans l'ensemble d'arrivée 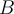 , on obtient ce qu'on appelle le produit cartésien de
, on obtient ce qu'on appelle le produit cartésien de 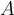 par
par 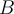 .
.
On le note :
Une relation 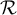 est en fait un sous-ensemble de
est en fait un sous-ensemble de 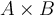 .
.
Dans notre exemple, 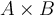 est un ensemble contenant 6 couples
est un ensemble contenant 6 couples 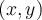 :
:
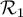 et
et 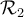 sont donc des sous-ensembles de
sont donc des sous-ensembles de 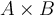 contenant chacun respectivement 2 et 3 couples.
contenant chacun respectivement 2 et 3 couples.
Certaines relations sont appelées fonctions. Pour cela, elles doivent posséder la caractéristique suivante :
Dans notre exemple, 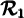 est une fonction, tandis que
est une fonction, tandis que 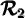 n'en est pas une puisque l'on y retrouve les couples
n'en est pas une puisque l'on y retrouve les couples 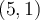 et
et 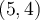 . En effet, dans le diagramme de
. En effet, dans le diagramme de 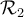 on remarque que l'élément
on remarque que l'élément 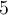 de l'ensemble
de l'ensemble  est relié à 2 éléments de l'ensemble
est relié à 2 éléments de l'ensemble  .
.
En général, nous nous intéressons aux fonctions réelles, c'est-à-dire aux fonctions dont les éléments de  et
et  appartiennent à
appartiennent à  . De telles fonctions sont égales à un ensemble de couples ordonnés de nombres réels. Pour préciser les ensembles de départ
. De telles fonctions sont égales à un ensemble de couples ordonnés de nombres réels. Pour préciser les ensembles de départ 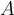 et d'arrivée
et d'arrivée 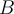 d'une fonction, on note
d'une fonction, on note 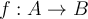 . Si l'on écrit
. Si l'on écrit 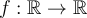 ,
,  est alors définie comme étant une fonction réelle.
est alors définie comme étant une fonction réelle.
La variable  se nomme la variable indépendante. On peut lui attribuer une valeur arbitraire choisie dans
se nomme la variable indépendante. On peut lui attribuer une valeur arbitraire choisie dans 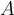 . Mais à partir du moment où la valeur de
. Mais à partir du moment où la valeur de  est déterminée, la valeur de
est déterminée, la valeur de  ou
ou 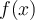 dépend de
dépend de  . On dit alors que
. On dit alors que  est la variable dépendante.
est la variable dépendante.
2. Domaine et image
Les fonctions sont souvent exprimées par une équation qui relie la variable  à son image. Ainsi, lorsque l'on veut déterminer l'image de
à son image. Ainsi, lorsque l'on veut déterminer l'image de 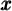 par la fonction
par la fonction 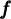 , il suffit de remplacer
, il suffit de remplacer  dans l'équation par sa valeur ou son expression afin d'obtenir son image
dans l'équation par sa valeur ou son expression afin d'obtenir son image 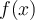 ou
ou  .
.
On peut imaginer que la fonction  agit comme une machine qui effectue une transformation de
agit comme une machine qui effectue une transformation de  .
.
Exemple :
Considérons la fonction réelle 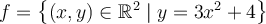 .
.
Lorsque l'on introduit  dans la machine
dans la machine  , celle-ci fait subir à
, celle-ci fait subir à  les transformations de l'opération
les transformations de l'opération 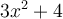 afin d'obtenir
afin d'obtenir 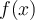 à la sortie. C'est-à-dire que
à la sortie. C'est-à-dire que  est élevé au carré, ensuite le résultat est multiplié par 3 et finalement, ce dernier est ajouté à 4.
est élevé au carré, ensuite le résultat est multiplié par 3 et finalement, ce dernier est ajouté à 4.
Ainsi, si on y introduit :
Il existe également plusieurs fonctions pour lesquelles une valeur réelle  ne possède pas d'image réelle
ne possède pas d'image réelle 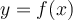 .
.
Exemple :
Par conséquent, l'équation 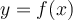 qui définit la relation qui existe entre les variables réelles
qui définit la relation qui existe entre les variables réelles  et
et  permet de déterminer quels éléments de l'ensemble de départ
permet de déterminer quels éléments de l'ensemble de départ  possèdent une image dans l'ensemble d'arrivée
possèdent une image dans l'ensemble d'arrivée  . L'ensemble des éléments possédant une image forme le domaine de la fonction
. L'ensemble des éléments possédant une image forme le domaine de la fonction  et l'ensemble des images forme le codomaine de la fonction
et l'ensemble des images forme le codomaine de la fonction  .
.
3. Graphique d'une fonction
Chaque couple 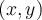 appartenant à une fonction réelle
appartenant à une fonction réelle  peut être représenté par un point dans le plan cartésien.
peut être représenté par un point dans le plan cartésien.  est alors l'abcisse et
est alors l'abcisse et  l'ordonnée du point dans le plan. On peut ainsi donner une représentation graphique d'une fonction qui dépend notamment de son domaine et de son équation.
l'ordonnée du point dans le plan. On peut ainsi donner une représentation graphique d'une fonction qui dépend notamment de son domaine et de son équation.
Exemple :
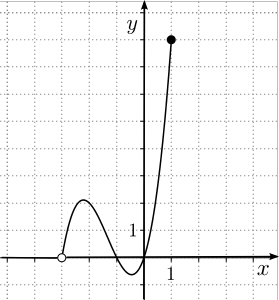
Le graphique ci-contre représente la fonction 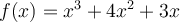 , où le
, où le ![\text{dom}f = \left]{-3,1}\right]. \text{dom}f = \left]{-3,1}\right].](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/a49914b0c0a9f5bcb62d3e9d39f3bf18.png)
Puisque le domaine est l'intervalle réel ![\left]{-3,1}\right], \left]{-3,1}\right],](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6360ae1fb0eba421f34bf4d5c1455cc6.png) le graphique est constitué d'une infinité de points. À partir d'un tableau de valeurs, il est possible d'obtenir quelques points du graphique en remplaçant les valeurs de
le graphique est constitué d'une infinité de points. À partir d'un tableau de valeurs, il est possible d'obtenir quelques points du graphique en remplaçant les valeurs de  dans l'équation.
dans l'équation.
 |
 |
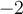 |
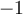 |
 |
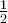 |
 |
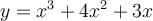 |
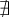 |
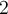 |
 |
 |
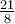 |
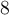 |
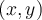 |
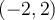 |
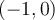 |
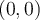 |
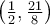 |
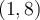 |
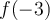 n'est pas défini, puisque
n'est pas défini, puisque 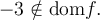 On indique donc un point vide
On indique donc un point vide 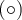 à l'extrémité gauche du graphique.
à l'extrémité gauche du graphique.
Puisque 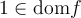 , on peut calculer
, on peut calculer 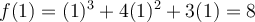 et on place un point plein
et on place un point plein  à l'autre extrémité pour indiquer que le point
à l'autre extrémité pour indiquer que le point 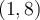 appartient à la courbe.
appartient à la courbe.
Un tableau de valeurs est utile pour tracer une esquisse, mais il ne permet pas de connaître avec certitude la forme de la courbe entre ces points. Nous verrons plus loin quelques modèles de fonctions courantes et les caractéristiques de leur graphique.
Test de la droite verticale
Le test de la droite verticale nous permet de déterminer si un graphique représente une fonction et non seulement une relation.
Par exemple :
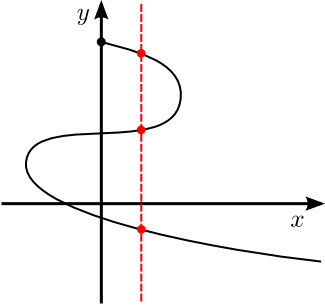
Le graphique ci-contre n'est pas celui d'une fonction, car il existe entre autres une droite verticale qui coupe la courbe en trois points, soit plus d'un point.
Le graphique d'une fonction peut révéler plusieurs informations. On peut par exemple visualiser :
- Le domaine et le codomaine;
- Les points qui croisent les axes de coordonnées;
- Le signe de la fonction;
- Les extremums de la fonction.
Exemple :
-
 Cochez la case dom f, puis faites bouger le curseur « Valeur de x ». Le tracé en rouge correspond aux valeurs de
Cochez la case dom f, puis faites bouger le curseur « Valeur de x ». Le tracé en rouge correspond aux valeurs de  possédant une image
possédant une image 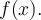
-
 Cochez la case codom f, puis faites bouger le curseur « Valeur de x ». Le tracé en vert correspond aux valeurs de
Cochez la case codom f, puis faites bouger le curseur « Valeur de x ». Le tracé en vert correspond aux valeurs de 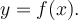
-
 En cochant la case Signe de la fonction et en modifiant toujours la valeur de
En cochant la case Signe de la fonction et en modifiant toujours la valeur de  , vous pouvez voir lorsque la fonction est positive et lorsqu'elle est négative. En effet, pour tout
, vous pouvez voir lorsque la fonction est positive et lorsqu'elle est négative. En effet, pour tout 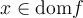 :
:
4. Points d'intersection avec les axes
Les points d'intersection avec les axes présentent un intérêt particulier pour l'analyse d'une fonction. Ces points sont appelés abcisse à l'origine et ordonnée à l'origine.
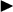 Abcisse à l'origine
Abcisse à l'origine
Les points d'intersection du graphique d'une fonction  avec l'axe horizontal sont tous les points du graphique de la forme
avec l'axe horizontal sont tous les points du graphique de la forme 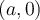 .
.
De plus, la valeur  est un zéro de la fonction
est un zéro de la fonction  , car
, car 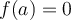 . Ainsi, le nombre de points d'intersection du graphique avec l'axe des
. Ainsi, le nombre de points d'intersection du graphique avec l'axe des  est égal au nombre de zéros de la fonction. On peut en déduire que si une fonction n'a aucun zéro, son graphique ne coupe jamais l'axe horizontal.
est égal au nombre de zéros de la fonction. On peut en déduire que si une fonction n'a aucun zéro, son graphique ne coupe jamais l'axe horizontal.
 est une valeur de
est une valeur de  appartenant au domaine de
appartenant au domaine de  pour laquelle
pour laquelleDe plus, par le théorème de factorisation,
 est un zéro de la fonction
est un zéro de la fonction 

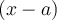 est un facteur de
est un facteur de 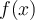 .
.Par conséquent, si une fonction est définie par un produit de facteurs, on peut facilement trouver ses zéros.
Exemple :
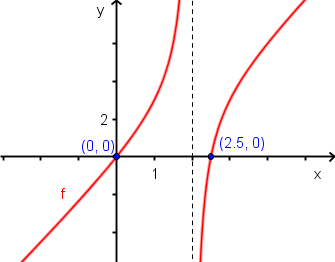
Trouvons, si possible, les zéros de la fonction 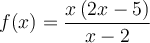 .
.
Pour trouver les zéros de la fonction  , il suffit de trouver les solutions de l'équation
, il suffit de trouver les solutions de l'équation 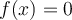 qui appartiennent au domaine.
qui appartiennent au domaine.
Étant donné que ces deux valeurs appartiennent au domaine, la fonction possède deux zéros : 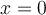 et
et 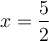 .
.
Les points 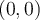 et
et 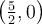 sont donc les points où la courbe croise l'axe des
sont donc les points où la courbe croise l'axe des  .
.
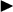 Ordonnée à l'origine
Ordonnée à l'origine
Ce point d'intersection est unique, car la valeur 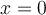 ne peut avoir qu'une seule image par la fonction
ne peut avoir qu'une seule image par la fonction  .
.
Exemple :
Soit la fonction 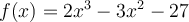 . Trouvons, si possible, tous les zéros de la fonction
. Trouvons, si possible, tous les zéros de la fonction  sachant que le point
sachant que le point 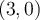 est une abscisse à l'origine.
est une abscisse à l'origine.
Il faut d'abord factoriser le polynôme 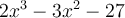 afin de résoudre l'équation
afin de résoudre l'équation  .
.
Étant donné que  est une solution de l'équation, alors par le théorème de factorisation,
est une solution de l'équation, alors par le théorème de factorisation, 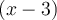 est un facteur de
est un facteur de 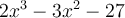 . Nous obtenons donc que
. Nous obtenons donc que
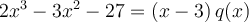 , où
, où 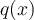 est un polynôme de degré
est un polynôme de degré 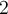 .
.
Nous pouvons trouver le polynôme 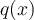 en effectuant la division suivante:
en effectuant la division suivante:
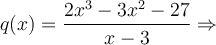 |
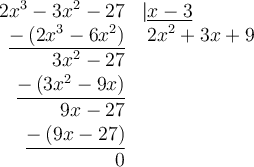 |
On peut donc écrire 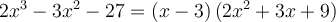 .
.
Or, le polynôme 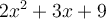 est non factorisable, car son discriminant
est non factorisable, car son discriminant 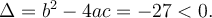
Alors 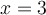 est la seule solution de l'équation
est la seule solution de l'équation 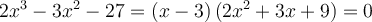 .
.
Donc la fonction 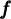 possède comme seul zéro
possède comme seul zéro 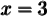 .
.
De plus, l'ordonnée à l'origine est 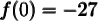 . Ainsi, le graphique coupe l'axe des
. Ainsi, le graphique coupe l'axe des  au point
au point 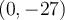 .
.
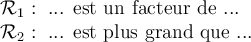
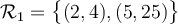
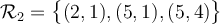
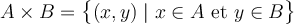
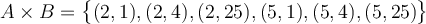
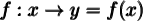
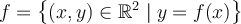
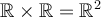
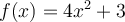
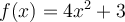
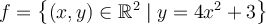
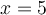
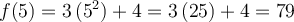
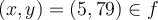
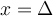

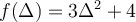
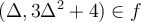
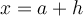
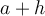
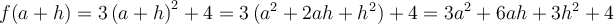
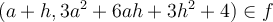
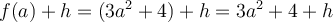
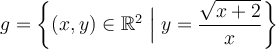
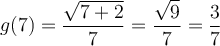
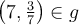
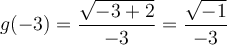
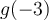
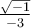
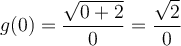
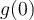
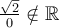
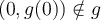
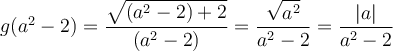
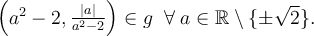
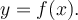
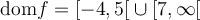
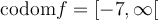
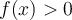
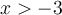
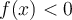
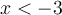
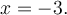
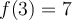
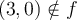
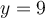
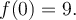
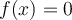
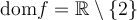
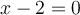
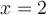
![\begin{array}{lcl} \dfrac{x\left({2x-5}\right)}{x-2} =0 & \Leftrightarrow & x\left({2x-5}\right)=0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } 2x-5 = 0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } x = \frac{5}{2} \end{array} \begin{array}{lcl} \dfrac{x\left({2x-5}\right)}{x-2} =0 & \Leftrightarrow & x\left({2x-5}\right)=0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } 2x-5 = 0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } x = \frac{5}{2} \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6aa5aff29220bfa7b9ebef9c1d3632e6.png)