2.2 Les fonctions algébriques
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 2.2 Les fonctions algébriques |
| Imprimé par: | Visiteur anonyme |
| Date: | vendredi 17 mai 2024, 23:52 |
Description
- Fonction linéaire (droite)
- Fonction quadratique (parabole)
- Fonction puissance (exposant naturel)
- Fonction rationnelle
- Fonction racine et exposant fractionnaire
- Trouver le domaine d'une fonction algébrique
1. Fonction linéaire (droite)
Le graphique GeoGebra suivant nous permet d'étudier plus en détail la fonction linéaire afin d'observer plusieurs de ses caractéristiques.
-
Le graphique de la fonction est représenté par une droite ni verticale, ni horizontale.
-
La fonction coupe l'axe des abcisses au point
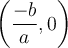 et possède donc un seul zéro.
et possède donc un seul zéro.Elle coupe l'axe des ordonnées au point
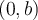 .
.  Déplacez le curseur « b » afin de remarquer l'effet sur le graphique de différentes valeurs de
Déplacez le curseur « b » afin de remarquer l'effet sur le graphique de différentes valeurs de 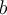 .
. -
La pente
 de la droite indique la variation de
de la droite indique la variation de  pour chaque accroissement de 1 unité de
pour chaque accroissement de 1 unité de  .
. Déplacez le curseur « a » afin de modifier sa valeur. Nous remarquons que :
Déplacez le curseur « a » afin de modifier sa valeur. Nous remarquons que : -
La pente d'une fonction linéaire est constante, c'est-à-dire qu'elle a la même valeur, quels que soient les points de la droite entre lesquels on la calcule.
Si
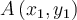 et
et 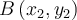 sont deux points de cette droite, alors
sont deux points de cette droite, alors En déplaçant le point A sur la droite, vous pouvez remarquez que ce rapport demeure constant.
En déplaçant le point A sur la droite, vous pouvez remarquez que ce rapport demeure constant.
On peut tracer le graphique d'une droite ou trouver son équation soit à l'aide de deux points ou à l'aide d'un point et de la pente. Voici quelques exemples.
2. Fonction quadratique (parabole)
Le graphique de la fonction est représenté par une parabole. À partir du graphique GeoGebra suivant, étudions plus en détail la fonction quadratique afin d'observer plusieurs de ses caractéristiques.
-
L'orientation de la parabole est déterminée par le paramètre
 .
.Son ouverture est vers le haut si
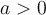 et vers le bas si
et vers le bas si 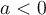 .
. Déplacez le curseur « a » afin de remarquer l'effet sur l'ouverture de la parabole pour différentes valeurs de
Déplacez le curseur « a » afin de remarquer l'effet sur l'ouverture de la parabole pour différentes valeurs de  .
.  Cochez la case Ordonnée. L'ordonnée à l'origine est le point
Cochez la case Ordonnée. L'ordonnée à l'origine est le point 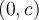 .
.
Déplacez le curseur « c » afin de remarquer l'effet sur le graphique pour différentes valeurs de
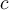 . La parabole se déplace parallèlement à l'axe des
. La parabole se déplace parallèlement à l'axe des  .
.-
 Cochez la case Sommet. Le sommet de la parabole est le point
Cochez la case Sommet. Le sommet de la parabole est le point 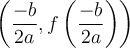 . En effet, il y a un axe de symétrie en
. En effet, il y a un axe de symétrie en 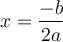 . Tout point de la parabole possède donc un deuxième point symétrique.
. Tout point de la parabole possède donc un deuxième point symétrique.En déplaçant le curseur « b », vous remarquez que l'axe de symétrie se déplace, mais que la distance entre les points symétriques reste la même. De plus, si
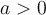 , le sommet est un minimum et si
, le sommet est un minimum et si 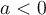 , le sommet est un maximum.
, le sommet est un maximum. - Les zéros de la parabole sont les solutions de l'équation
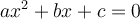 . On peut trouver, s'ils existent, les zéros de la fonction par la formule quadratique
. On peut trouver, s'ils existent, les zéros de la fonction par la formule quadratique 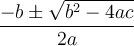 ou par la factorisation.
ou par la factorisation.
On appelle le discriminant
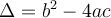 . Il aide à déterminer le nombre de zéros que possède la fonction.
. Il aide à déterminer le nombre de zéros que possède la fonction.  Cochez la case Zéro(s) et déplacez les différents curseurs « a », « b » et « c ».
Cochez la case Zéro(s) et déplacez les différents curseurs « a », « b » et « c ».-
Si
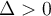 , la fonction possède deux zéros,
, la fonction possède deux zéros,  et
et 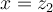 tels que
tels queOn peut exprimer la fonction en factorisant le polynôme sous la forme
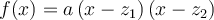 .
. Ex. : Choisissez a = 2, b = 3 et c = -5. Les zéros de la parabole sont
Ex. : Choisissez a = 2, b = 3 et c = -5. Les zéros de la parabole sont 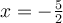 et
et 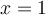 . En factorisant, on obtient
. En factorisant, on obtient 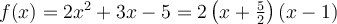 . Le discriminant
. Le discriminant 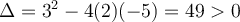 .
. -
Si
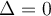 , la fonction possède un zéro
, la fonction possède un zéro  situé au sommet de la parabole.
situé au sommet de la parabole.On peut exprimer la fonction en factorisant le polynôme sous la forme
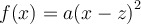 .
. Ex. : Choisissez a = 1, b = -6 et c = 9. La parabole possède un seul zéro en
Ex. : Choisissez a = 1, b = -6 et c = 9. La parabole possède un seul zéro en 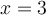 . En factorisant, on obtient
. En factorisant, on obtient 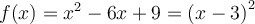 . Le discriminant
. Le discriminant 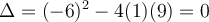 .
. -
Si
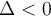 , la fonction ne possède aucun zéro. On ne peut factoriser le polynôme
, la fonction ne possède aucun zéro. On ne peut factoriser le polynôme 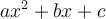 .
. Ex. : Choisissez a = 1 et b = 2. En déplaçant le curseur « c », on a que pour les valeurs
Ex. : Choisissez a = 1 et b = 2. En déplaçant le curseur « c », on a que pour les valeurs 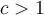 , la parabole ne possède aucun zéro. En effet, le discriminant
, la parabole ne possède aucun zéro. En effet, le discriminant 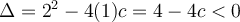 si
si 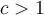 .
.
-
L'équation d'une parabole peut aussi être exprimée sous la forme canonique. Cette forme sera explorée plus en détails à partir du graphique GeoGebra dans la section des fonctions puissances.
On peut tracer le graphique d'une fonction quadratique à partir des éléments précédents. Voici quelques exemples.
3. Fonction puissance (exposant naturel)
Si  est un entier négatif, il s'agit de fonctions rationnelles et elles seront traitées dans la prochaine section. Les exposants de la forme
est un entier négatif, il s'agit de fonctions rationnelles et elles seront traitées dans la prochaine section. Les exposants de la forme 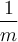 , les fonctions racines, et les exposants réels seront également abordés plus loin. Les fonctions puissances à exposant naturel, celles qui nous intéressent, servent de base dans la construction des fonctions polynomiales de degré
, les fonctions racines, et les exposants réels seront également abordés plus loin. Les fonctions puissances à exposant naturel, celles qui nous intéressent, servent de base dans la construction des fonctions polynomiales de degré  de la forme :
de la forme :
où les coefficients 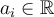 pour tout
pour tout 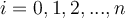 ,
, 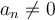 et
et 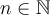 .
.
À partir du graphique GeoGebra suivant, étudions plus en détails les caractéristiques des fonctions puissances pour différentes valeurs de  .
.
Les premières valeurs de  correspondent à des fonctions de base :
correspondent à des fonctions de base :
- Pour
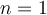 , c'est la fonction linéaire
, c'est la fonction linéaire 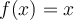 .
. - Pour
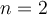 , c'est la fonction quadratique
, c'est la fonction quadratique 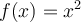 .
. - Pour
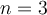 , c'est la fonction cubique
, c'est la fonction cubique 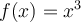 .
. - Si
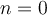 , on aura la fonction constante
, on aura la fonction constante 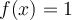 .
.
Toutes ces fonctions ont comme point commun 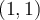 .
. ![]() Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique d'une augmentation ou d'une diminution de l'exposant.
Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique d'une augmentation ou d'une diminution de l'exposant.
On peut séparer les fonctions puissances en deux catégories, selon que l'exposant  est pair ou impair.
est pair ou impair.
- Pour
 pair,
pair, 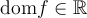
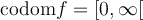 .
.- La fonction possède l'axe des
 comme axe de symétrie.
comme axe de symétrie. - Elle possède un seul zéro en
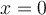 et il s'agit d'un minimum.
et il s'agit d'un minimum. - Pour
 impair,
impair,
On peut également créer d'autres fonctions composées à partir des fonctions puissances de base. Nous élaborerons ce concept plus en détail dans la section sur les transformations de fonctions. Pour l'instant, dans le graphique Geogebra, on s'intéresse aux fonctions de la forme
![]() Déplacez les différents curseurs « a », « h » et « k ».
Déplacez les différents curseurs « a », « h » et « k ».
![]() Ex. : Choisissez la fonction de base
Ex. : Choisissez la fonction de base 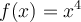 . Si
. Si 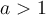 , la fonction décroit et croit plus rapidement que la fonction
, la fonction décroit et croit plus rapidement que la fonction 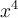 (la courbe se comprime sur l'axe des
(la courbe se comprime sur l'axe des  ). Si
). Si 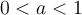 , la fonction décroit et croit moins rapidement. De plus, pour
, la fonction décroit et croit moins rapidement. De plus, pour 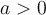 , la fonction est positive et pour
, la fonction est positive et pour 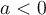 , la fonction est négative.
, la fonction est négative.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 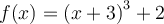 . On remarque le graphique de la fonction de base
. On remarque le graphique de la fonction de base 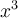 subit un déplacement vers la gauche de
subit un déplacement vers la gauche de 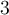 et vers le haut de
et vers le haut de 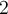 . Donc le point
. Donc le point 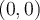 s'est déplacé au point
s'est déplacé au point 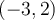 .
.
Par conséquent, on peut généraliser les résultats précédents.
4. Fonction rationnelle
Tout comme les fonctions puissances, les graphiques des fonctions rationnelles peuvent prendre différentes formes selon les degrés des polynômes. Tracer le graphique de telles fonctions peut s'avérer complexe. Le cours de Calcul différentiel nous permettra d'analyser plusieurs caractéristiques de ces courbes dont les intervalles de croissance et de décroissance, les extremums et le sens de la concavité.
À partir du graphique GeoGebra suivant, nous allons tout d'abord étudier en détails les caractéristiques des fonctions rationnelles de base de la forme
![]() Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique de l'augmentation ou de la diminution de l'exposant. Les premières valeurs de
Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique de l'augmentation ou de la diminution de l'exposant. Les premières valeurs de  correspondent aux fonctions suivantes :
correspondent aux fonctions suivantes :
Voici quelques caractéristiques communes de ces fonctions.
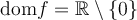 .
.- Toutes ces fonctions ont comme asymptote verticale
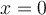 et comme asymptote horizontale
et comme asymptote horizontale 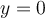 . Le centre du graphique est le point d'intersection des deux asymptotes, soit le point
. Le centre du graphique est le point d'intersection des deux asymptotes, soit le point 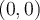 .
. - Elles n'ont aucun zéro ni ordonnée à l'origine.
- Elles possèdent aucun minimum ni maximum.
On peut également créer d'autres fonctions composées à partir des fonctions rationnelles de base. Nous élaborerons ce concept plus en détail dans la section sur les transformations de fonctions. Pour l'instant, dans le graphique Geogebra, on s'intéresse aux fonctions de la forme
![]() Déplacez les différents curseurs « a », « h » et « k ».
Déplacez les différents curseurs « a », « h » et « k ».
![]() Ex. : Choisissez la fonction de base
Ex. : Choisissez la fonction de base 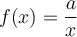 . Si
. Si 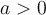 , la fonction est décroissante sur son domaine et est positive sur l'intervalle
, la fonction est décroissante sur son domaine et est positive sur l'intervalle ![\left]{0, \infty}\right[ \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d13a6e4c304d2f4a427dad83ef19750a.png) . Si
. Si 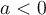 , la fonction est croissante sur son domaine et est positive sur l'intervalle
, la fonction est croissante sur son domaine et est positive sur l'intervalle ![\left]{-\infty, 0}\right[ \left]{-\infty, 0}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/da7e2fe2d02a9ece3c4691a384fe1f74.png) .
.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 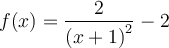 . On remarque que tous les points du graphique de base
. On remarque que tous les points du graphique de base 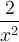 subissent un déplacement vers la gauche de
subissent un déplacement vers la gauche de  et vers le bas de
et vers le bas de 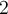 . Le centre
. Le centre 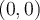 se déplace donc au point
se déplace donc au point 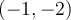 . Ainsi,
. Ainsi, 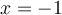 est l'asymptote verticale et
est l'asymptote verticale et 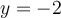 est l'asymptote horizontale.
est l'asymptote horizontale.
Par conséquent, on peut généraliser les résultats précédents.
Nous nous intéressons également au domaine des fonctions rationnelles. Les sections sur la simplification de fractions rationnelles et sur la résolution d'équations contenant des fractions rationnelles nous aideront particulièrement.
Voici quelques exemples de fonctions intéressantes, ainsi que leur représentation graphique.
5. Fonction racine et exposant fractionnaire
Comme nous avons vu dans une section précédente, les fonctions de la forme 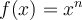 sont appelées fonctions puissances. Si l'exposant est un nombre fractionnaire, cela signifie que la fonction est irrationnelle et, dans son équation, la variable indépendante apparaît sous un radical.
sont appelées fonctions puissances. Si l'exposant est un nombre fractionnaire, cela signifie que la fonction est irrationnelle et, dans son équation, la variable indépendante apparaît sous un radical.
Voici la définition et le graphique de quelques fonctions à exposant fractionnaire.
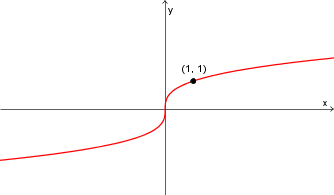
![f(x) = x^{1/3} = \sqrt[3]{x} f(x) = x^{1/3} = \sqrt[3]{x}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1f88f99349b9b43ffb704dfc00690fdb.png) 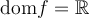 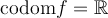 |
 |
![f(x) = x^{2/3} = \sqrt[3]{x^2} f(x) = x^{2/3} = \sqrt[3]{x^2}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cf72359649a6fb5f3a0fb6ad5cb7fb21.png) 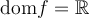 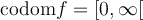 |
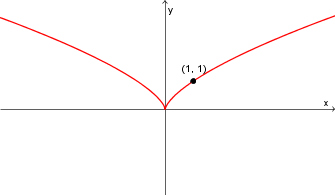 |
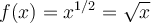 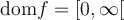 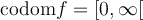 |
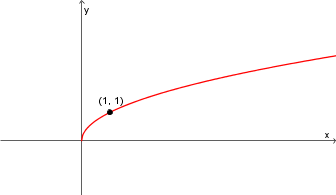 |
Étudions plus en détail cette dernière fonction, soit la fonction racine carrée
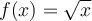 . Pour définir la fonction racine carrée, on peut faire appel à la réciproque de la fonction quadratique
. Pour définir la fonction racine carrée, on peut faire appel à la réciproque de la fonction quadratique 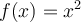 . Ce sujet est abordé dans une autre section. Contentons-nous d'explorer les caractéristiques de la fonction racine à partir du graphique GeoGebra suivant.
. Ce sujet est abordé dans une autre section. Contentons-nous d'explorer les caractéristiques de la fonction racine à partir du graphique GeoGebra suivant.La fonction racine carrée de base 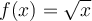 possède les caractéristiques suivantes:
possède les caractéristiques suivantes:
- La fonction possède un seul zéro en
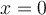 et il s'agit d'un minimum.
et il s'agit d'un minimum. - Elle est croissante sur tout son domaine, soit sur
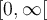 .
. - Elle est positive sur
![\left]{0, \infty}\right[ \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d13a6e4c304d2f4a427dad83ef19750a.png) et nulle si
et nulle si 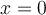 . Elle n'est jamais négative.
. Elle n'est jamais négative.
On peut également créer d'autres fonctions composées à partir de la fonction racine de base. Nous élaborerons ce concept plus en détails dans la section sur les transformations de fonctions. Pour l'instant, dans le graphique Geogebra, on s'intéresse aux fonctions de la forme
![]() Déplacez les différents curseurs « a », « b », « h » et « k ».
Déplacez les différents curseurs « a », « b », « h » et « k ».
- Le paramètre
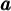 déforme verticalement la fonction racine de base. De plus, si
déforme verticalement la fonction racine de base. De plus, si  change de signe, la courbe subit une réflexion par rapport à l'axe des
change de signe, la courbe subit une réflexion par rapport à l'axe des 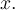
- Le paramètre
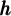 fait subir à la fonction
fait subir à la fonction 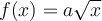 une translation horizontale et le paramètre
une translation horizontale et le paramètre 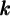 , une translation verticale.
, une translation verticale. - Si
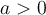 , le point
, le point 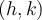 est un minimum et si
est un minimum et si  , le point
, le point 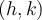 est un maximum.
est un maximum. - Le paramètre
 déforme horizontalement la fonction racine de base. Par contre, si
déforme horizontalement la fonction racine de base. Par contre, si 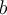 change de signe, la courbe subit une réflexion par rapport à la droite verticale passant par le sommet
change de signe, la courbe subit une réflexion par rapport à la droite verticale passant par le sommet 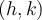 .
. - La règle de transformation appliquée au graphique de la fonction de base est :
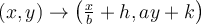 . Tous les points
. Tous les points 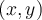 de la fonction
de la fonction 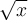 sont transformés par cette règle.
sont transformés par cette règle.
Dans le graphique Geogebra, cela est illustré par le point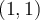 de la fonction
de la fonction 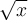 pointillée qui s'est déplacé au point P.
pointillée qui s'est déplacé au point P.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 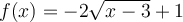 .
.
On a que 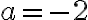 et
et 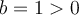 . La courbe est donc décroissante, car elle a subit une réflexion verticale. On remarque aussi que tous les points du graphique
. La courbe est donc décroissante, car elle a subit une réflexion verticale. On remarque aussi que tous les points du graphique 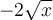 subissent un déplacement vers la droite de
subissent un déplacement vers la droite de 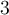 et vers le haut de
et vers le haut de  . L'extrémité
. L'extrémité 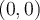 s'est donc déplacé au point
s'est donc déplacé au point 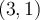 . Il s'agit d'un maximum.
. Il s'agit d'un maximum.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 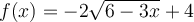 .
.
En effectuant une mise en évidence, on a que 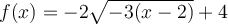 . Ainsi,
. Ainsi, 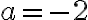 et
et 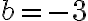 . La courbe est donc croissante, car elle a subit une réflexion verticale et une réflexion horizontale. De plus, le sommet
. La courbe est donc croissante, car elle a subit une réflexion verticale et une réflexion horizontale. De plus, le sommet 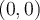 s'est déplacé au point
s'est déplacé au point 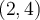 . Il s'agit d'un minimum.
. Il s'agit d'un minimum.
6. Trouver le domaine d'une fonction algébrique
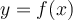 , l'ensemble des éléments
, l'ensemble des éléments  possédant une image réelle
possédant une image réelle  forment le domaine de la fonction
forment le domaine de la fonction  .
.Pour trouver le domaine d'une fonction algébrique quelconque, il faut toujours s'assurer de respecter ces deux restrictions. Voici quelques exemples.
Exemples : Trouvons le domaine des fonctions suivantes.
Le domaine de cette fonction dépend des deux restrictions suivantes :
-
Le dénominateur doit être non nul, c'est-à-dire
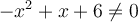 . Trouvons ces valeurs en factorisant :
. Trouvons ces valeurs en factorisant : -
L'expression à l'intérieur de la racine carrée doit être non-négative, c'est-à-dire
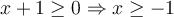 .
.

En combinant ces deux restrictions (voir la droite des réels ci-dessus), on obtient le domaine de  , soit
, soit ![\text{dom }f = \left[-1,3\right[ \cup \left] 3, \infty \right[ \text{dom }f = \left[-1,3\right[ \cup \left] 3, \infty \right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9e06f3805607c907e8a6b502aa725815.png) . On remarque que
. On remarque que 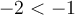 et il s'agit donc d'une valeur qui est déjà enlevée à cause de la deuxième restriction.
et il s'agit donc d'une valeur qui est déjà enlevée à cause de la deuxième restriction.
Voici un dernier exemple de détermination du domaine d'une fonction algébrique où nous avons recours à un tableau de signes pour résoudre une inéquation. Pour revoir les notions théoriques sur cette méthode, visitez la page « Résoudre une inéquation à l'aide d'un tableau de signes ».
Pour respecter la première restriction, il faut résoudre l'inéquation 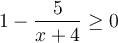 . En transformant cette inéquation sous la forme
. En transformant cette inéquation sous la forme 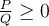 , on obtient :
, on obtient :
Sachant que le numérateur 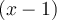 est nul si
est nul si 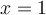 et que le dénominateur
et que le dénominateur 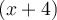 est nul si
est nul si 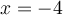 , on peut remplir le tableau de signes suivant pour résoudre l'inéquation.
, on peut remplir le tableau de signes suivant pour résoudre l'inéquation.
![\left]{-\infty,-4}\right[ \left]{-\infty,-4}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c4873b204332e00af88b94a6d93340db.png) |
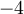 |
![\left]{-4,1}\right[ \left]{-4,1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d853a16c2f5c3a62322fa6fe5407431a.png) |
 |
![\left]{1,\infty}\right[ \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1c8404c763714ff8de9f14e488b459df.png) |
|
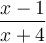 |
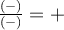 |
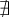 |
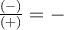 |
 |
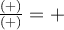 |
On obtient que ![\text{dom }f = \left]-\infty,-4\right[ \cup \left[1,\infty\right[ \text{dom }f = \left]-\infty,-4\right[ \cup \left[1,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7f2f97ff3a8115673a621ef4df7906e9.png) . On remarque que
. On remarque que 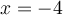 n'appartient pas au domaine de
n'appartient pas au domaine de  cette valeur entraîne un dénominateur nul.
cette valeur entraîne un dénominateur nul.
Voici un graphique Geogebra pour illustrer la fonction et le calcul d'images pour certaines valeurs de  .
. ![]() Déplacez le curseur b avec votre souris pour voir la valeur de l'image f(b). En même temps, le point bleu
Déplacez le curseur b avec votre souris pour voir la valeur de l'image f(b). En même temps, le point bleu 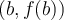 se déplace sur la courbe de la fonction
se déplace sur la courbe de la fonction 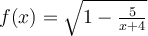 . Remarquez les valeurs de b qui font partie du domaine de
. Remarquez les valeurs de b qui font partie du domaine de  .
.
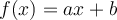
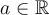
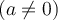
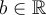
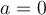
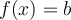
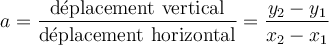
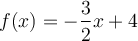
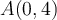
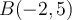
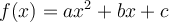
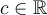
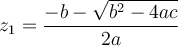
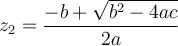
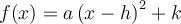
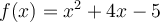
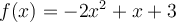
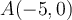
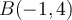
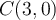
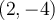
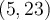
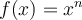
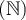
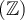
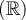
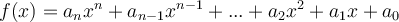
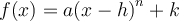
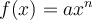
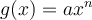
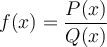
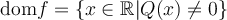
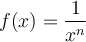
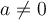
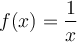
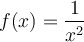
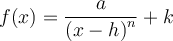
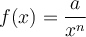
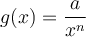
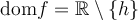
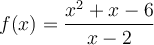
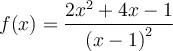
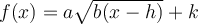
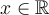
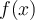
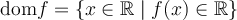
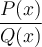
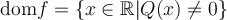
![\sqrt[n]{H(x)} \sqrt[n]{H(x)}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2e4f25b82acfaae56935615e04f58357.png)
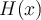
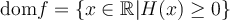
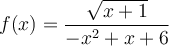
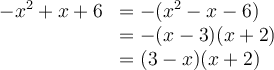
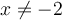
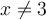
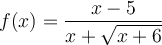
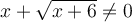
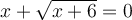

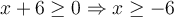
![\text{dom }f = \left[-6,-2\right[ \cup \left] -2,\infty\right[ \text{dom }f = \left[-6,-2\right[ \cup \left] -2,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6e01a1f84912e669f9112d32c5c0df09.png)
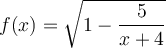
![\begin{array}{ll} 1-\dfrac{5}{x+4} \geq 0 & \Rightarrow \dfrac{(x+4)-5}{x+4} \geq 0\\[0.8em] &\Rightarrow \dfrac{x-1}{x+4} \geq 0 \end{array} \begin{array}{ll} 1-\dfrac{5}{x+4} \geq 0 & \Rightarrow \dfrac{(x+4)-5}{x+4} \geq 0\\[0.8em] &\Rightarrow \dfrac{x-1}{x+4} \geq 0 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7ba927fa01b6527924a868bd54114acd.png)