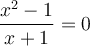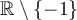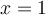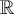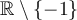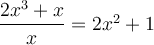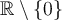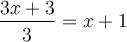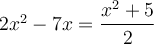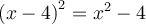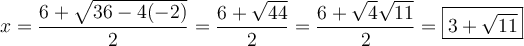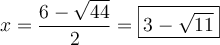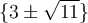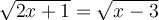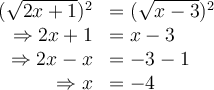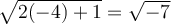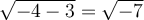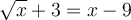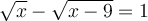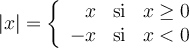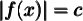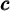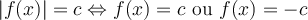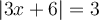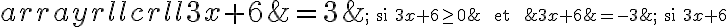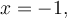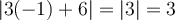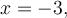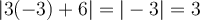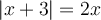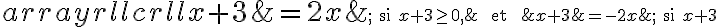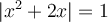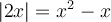1.4 Les équations
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 1.4 Les équations |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 20:37 |
Description
- Définitions
- Principes pour résoudre des équations
- Équations contenant des fractions rationnelles
- Équations contenant des racines carrées
- Équations contenant des valeurs absolues
1. Définitions
- Une équation est une égalité contenant une ou plusieurs variables. Elle peut être vraie ou fausse.
-
Le domaine d’une équation est l’ensemble des valeurs que peut prendre sa ou ses variables. Il faut tenir compte des restrictions applicables aux nombres réels.
- Pour trouver les solutions d’une équation, c'est-à-dire résoudre une équation, on doit trouver les valeurs du domaine qui rendent l'égalité vraie.
- Deux équations sont dites équivalentes si elles ont le même ensemble solution.
- Une identité est une équation qui est vraie pour chacune des valeurs de son domaine.
2. Principes pour résoudre des équations
- Utiliser les opérations élémentaires
 pour transformer l'équation initiale de façon à obtenir une ou plusieurs équations équivalentes de la forme
pour transformer l'équation initiale de façon à obtenir une ou plusieurs équations équivalentes de la forme  où
où 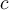 est une constante.
est une constante. - Ne jamais multiplier ou diviser une équation par 0.
- Toujours vérifier la solution dans l’équation initiale.
- Si une équation peut être transformée en une équation quadratique de la forme
 , il suffit de trouver les zéros du polynôme
, il suffit de trouver les zéros du polynôme 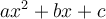 à l'aide d'une des deux méthodes suivantes :
à l'aide d'une des deux méthodes suivantes :- En factorisant (si possible) et en utilisant la règle du produit nul. Cette règle dit que le produit de deux ou plusieurs facteurs est égal à 0 si et seulement si l'un de ces facteurs est égal à 0
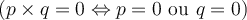 .
. - En utilisant la formule quadratique
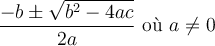 .
.
- En factorisant (si possible) et en utilisant la règle du produit nul. Cette règle dit que le produit de deux ou plusieurs facteurs est égal à 0 si et seulement si l'un de ces facteurs est égal à 0
Exemples : Résoudre les équations suivantes.
3. Équations contenant des fractions rationnelles
Lorsqu'une équation contient des fractions rationnelles, il faut d'abord bien déterminer le domaine.
Après avoir résolu l'équation, on doit vérifier si les solutions trouvées font partie du domaine.
Exemple : Résoudre l'équation 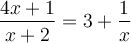 .
.
Résolution :
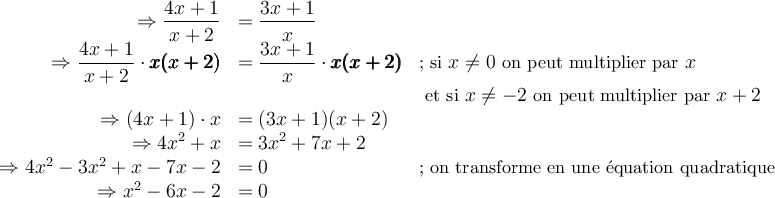
On peut peut utiliser la formule quadratique 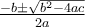 pour résoudre
pour résoudre 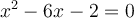 .
.
Ces deux valeurs appartiennent au domaine et vérifient l'équation initiale.
Exemples : Résoudre les équations suivantes.
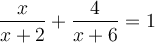
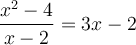
Exercices formatifs WeBWorK
 Résoudre des équations linéaires, quadratiques et rationnelles
Résoudre des équations linéaires, quadratiques et rationnelles
4. Équations contenant des racines carrées
Pour résoudre une équation contenant des racines carrées, on peut appliquer les principes suivants :
- Isoler un des termes comportant une racine carrée.
- Élever au carré les deux membres de chaque côté de l'égalité.
- Résoudre l'équation.
Mais attention, l'équation résultante n'est pas toujours équivalente à celle de départ. En effet, en élevant au carré les deux membres de l'équation, on peut créer des solutions fausses  , mais
, mais 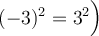 .
.
Il faut donc toujours vérifier chacune des solutions possibles dans l'équation initiale afin d'éliminer les solutions fausses.
Par exemple :
En élevant chaque membre au carré, on obtient :
Or, en remplaçant 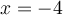 dans l'équation initiale, on obtient des racines carrées d'un nombre négatif, ce qui n'est pas défini. En effet,
dans l'équation initiale, on obtient des racines carrées d'un nombre négatif, ce qui n'est pas défini. En effet,
Ainsi, 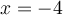 n'est pas une solution et par conséquent cette équation n'a pas de solution réelle.
n'est pas une solution et par conséquent cette équation n'a pas de solution réelle.
Exemples : Résoudre les équations suivantes.
Exercices formatifs WeBWorK
 Résoudre des équations contenant des racines carrées
Résoudre des équations contenant des racines carrées
5. Équations contenant des valeurs absolues
La valeur absolue d'un nombre  donne toujours un résultat positif. Par exemple,
donne toujours un résultat positif. Par exemple, 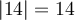 et
et 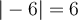 . Par définition, la fonction
. Par définition, la fonction 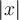 laisse positif tout nombre
laisse positif tout nombre  qui est déjà positif et rend positif tout nombre
qui est déjà positif et rend positif tout nombre  qui est négatif. On peut aussi la définir de la façon suivante :
qui est négatif. On peut aussi la définir de la façon suivante :
Cette façon de définir la valeur absolue est équivalente. En effet, dans les deux cas on obtient 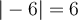 et
et 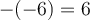 comme le montre le graphique Geogebra suivant.
comme le montre le graphique Geogebra suivant. ![]() Déplacez le point vert
Déplacez le point vert![]() sur la droite des réels et remarquez la définition de la valeur absolue selon que le nombre
sur la droite des réels et remarquez la définition de la valeur absolue selon que le nombre  est positif ou négatif.
est positif ou négatif.
Pour résoudre une équation contenant des valeurs absolues, on doit considérer deux cas possibles : si l'expression à l'intérieur est positive et si elle est négative.
La résolution des formes d'équations suivantes respecte ce principe.
Résolution d'une équation de la forme 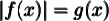
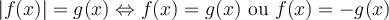
- On vérifie les solutions dans l'équation initiale et on rejette celles qui ne vérifient pas l'équation.
Comme le membre de droite n'est pas une constante mais contient une variable  , la valeur du membre de droite peut donc devenir négative, ce qui est interdit. Par conséquent, il est essentiel de vérifier si les solutions transforment l'équation en une égalité vraie.
, la valeur du membre de droite peut donc devenir négative, ce qui est interdit. Par conséquent, il est essentiel de vérifier si les solutions transforment l'équation en une égalité vraie.
Exemples : Résoudre les équations suivantes.
Selon la définition de la valeur absolue, résoudre cette équation revient à résoudre les deux équations suivantes :
Les deux solutions de cette équation sont  et
et  . On peut même le vérifier en remplaçant ces deux valeurs dans l'équation de départ.
. On peut même le vérifier en remplaçant ces deux valeurs dans l'équation de départ.
Étant donné que 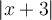 est toujours positif, il faut aussi que
est toujours positif, il faut aussi que 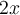 soit toujours positif. Ainsi, on a comme restriction :
soit toujours positif. Ainsi, on a comme restriction : 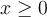 . On peut maintenant résoudre les deux équations suivantes :
. On peut maintenant résoudre les deux équations suivantes :
Or 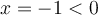 et par conséquent ne respecte pas la restriction. En effet, en remplaçant
et par conséquent ne respecte pas la restriction. En effet, en remplaçant 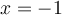 dans l'équation initiale, on obtient
dans l'équation initiale, on obtient
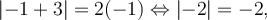 ce qui est faux. Par conséquent,
ce qui est faux. Par conséquent, 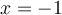 n'est pas une solution et
n'est pas une solution et  est la seule solution de l'équation.
est la seule solution de l'équation.
Exemples : Résoudre les équations suivantes.
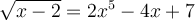
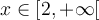
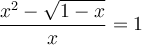
![x \in \left] {-\infty, 0} \right[ \cup \left] {0, 1} \right] x \in \left] {-\infty, 0} \right[ \cup \left] {0, 1} \right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0ee206997cd3abb3b75734ffd335ecd6.png)
![x \in \left] {-\infty, 1} \right] \setminus \{ 0\} x \in \left] {-\infty, 1} \right] \setminus \{ 0\}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/73a4506101b1da34afdb17e1cb9a5b58.png)