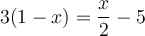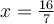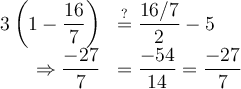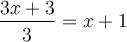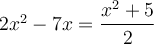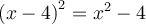1.4 Les équations
- Définitions
- Principes pour résoudre des équations
- Équations contenant des fractions rationnelles
- Équations contenant des racines carrées
- Équations contenant des valeurs absolues
2. Principes pour résoudre des équations
- Utiliser les opérations élémentaires
 pour transformer l'équation initiale de façon à obtenir une ou plusieurs équations équivalentes de la forme
pour transformer l'équation initiale de façon à obtenir une ou plusieurs équations équivalentes de la forme  où
où 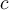 est une constante.
est une constante. - Ne jamais multiplier ou diviser une équation par 0.
- Toujours vérifier la solution dans l’équation initiale.
- Si une équation peut être transformée en une équation quadratique de la forme
 , il suffit de trouver les zéros du polynôme
, il suffit de trouver les zéros du polynôme 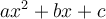 à l'aide d'une des deux méthodes suivantes :
à l'aide d'une des deux méthodes suivantes :- En factorisant (si possible) et en utilisant la règle du produit nul. Cette règle dit que le produit de deux ou plusieurs facteurs est égal à 0 si et seulement si l'un de ces facteurs est égal à 0
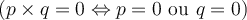 .
. - En utilisant la formule quadratique
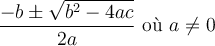 .
.
- En factorisant (si possible) et en utilisant la règle du produit nul. Cette règle dit que le produit de deux ou plusieurs facteurs est égal à 0 si et seulement si l'un de ces facteurs est égal à 0
Exemples : Résoudre les équations suivantes.