1.5 Les inéquations
- Principes pour résoudre une inéquation
- Résoudre une inéquation à l'aide d'un tableau de signes
- Résoudre une inéquation contenant des valeurs absolues
1. Principes pour résoudre une inéquation
Résoudre une inéquation consiste à trouver l'ensemble des valeurs par lesquelles on peut remplacer la variable pour obtenir une inégalité vraie. Par exemple :
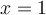 est une des solutions de l'inégalité
est une des solutions de l'inégalité 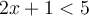 , car en la remplaçant dans cette dernière on obtient
, car en la remplaçant dans cette dernière on obtient 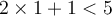 qui est une inégalité vraie.
qui est une inégalité vraie. Par contre
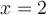 n'est pas une solution, car
n'est pas une solution, car 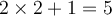 et
et 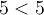 est une inégalité fausse.
est une inégalité fausse. On voit que les solutions de cette inéquation sont toutes les valeurs telles que
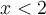 .
.Afin de résoudre une inéquation, il faut la transformer en une ou plusieurs inéquations équivalentes de la forme :
Pour y arriver, on peut bien sûr utiliser les opérations élémentaires  et
et 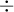 . Par contre, pour chacune des opérations il faut respecter certaines propriétés.
. Par contre, pour chacune des opérations il faut respecter certaines propriétés.
Exemples :
a) Trouvons l'ensemble solution de l'inéquation 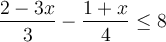
L'ensemble solution de cette inéquation est décrit par
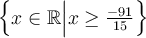 ou par l'intervalle
ou par l'intervalle 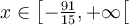 .
.
b) Trouvons le domaine de l'équation 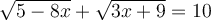
On cherche l'ensemble des valeurs de  pour lesquelles chacune des expressions existe dans
pour lesquelles chacune des expressions existe dans 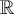 .
.
Puisque la racine carrée d'un nombre négatif n'est pas définie, il faut que
Le domaine est donc l'ensemble des valeurs pour lesquelles  et
et 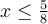 , ce qui correspond à l'intervalle
, ce qui correspond à l'intervalle ![\left[{-3, \frac{5}{8}}\right] \left[{-3, \frac{5}{8}}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/18304db4caf8272aa1b28c91c58d2a2d.png) .
.
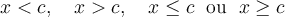
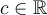
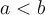
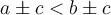
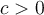
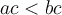
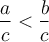
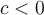
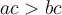
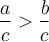
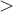
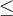
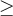
![\begin{array}{rcll} \dfrac{4\left({2-3x}\right) - 3\left({1+x}\right)}{12} & \leq & 8 & \small\text{; dénominateur commun} \\[1em]\dfrac{5-15x}{12} & \leq & 8 & {} \\[1em]5 - 15x & \leq & \pmb{12} \times 8 & \small\text{; on a multiplié par }12 \text{ chaque membre sans changer le sens de l'inégalité} \\[0.8em]-15x & \leq & 96 - \pmb{5} & \small\text{; on a soustrait }5 \text{ à chaque membre sans changer le sens de l'inégalité} \\[0.8em]x & \geq & \dfrac{91}{\pmb{-15}} & \small\text{; on a divisé par }-15 \text{ chaque membre }\textbf{en changeant le sens de l'inégalité} \end{array} \begin{array}{rcll} \dfrac{4\left({2-3x}\right) - 3\left({1+x}\right)}{12} & \leq & 8 & \small\text{; dénominateur commun} \\[1em]\dfrac{5-15x}{12} & \leq & 8 & {} \\[1em]5 - 15x & \leq & \pmb{12} \times 8 & \small\text{; on a multiplié par }12 \text{ chaque membre sans changer le sens de l'inégalité} \\[0.8em]-15x & \leq & 96 - \pmb{5} & \small\text{; on a soustrait }5 \text{ à chaque membre sans changer le sens de l'inégalité} \\[0.8em]x & \geq & \dfrac{91}{\pmb{-15}} & \small\text{; on a divisé par }-15 \text{ chaque membre }\textbf{en changeant le sens de l'inégalité} \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8bd54b5f1c3059ef520721fe769e20a1.png)
![\begin{array}{rclcrcl} 5-8x & \geq & 0 &\quad\text{ et }\quad& 3x+9 & \geq & 0 \\[0.8em]-8x & \geq & -5 & {} & 3x & \geq & -9 \\[0.8em]x & \mathbf{\leq} & \dfrac{5}{8} & {} & x & \geq & -3 \end{array} \begin{array}{rclcrcl} 5-8x & \geq & 0 &\quad\text{ et }\quad& 3x+9 & \geq & 0 \\[0.8em]-8x & \geq & -5 & {} & 3x & \geq & -9 \\[0.8em]x & \mathbf{\leq} & \dfrac{5}{8} & {} & x & \geq & -3 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f11aa3eafe1c6aa2fb7fd389052e9401.png)