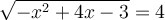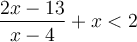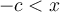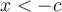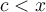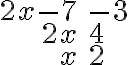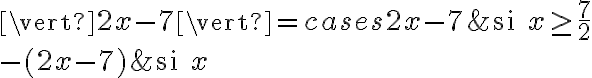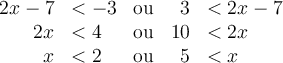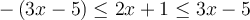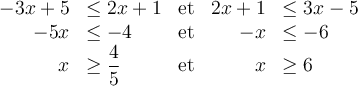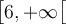1.5 Les inéquations
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 1.5 Les inéquations |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 09:17 |
Description
- Principes pour résoudre une inéquation
- Résoudre une inéquation à l'aide d'un tableau de signes
- Résoudre une inéquation contenant des valeurs absolues
1. Principes pour résoudre une inéquation
Résoudre une inéquation consiste à trouver l'ensemble des valeurs par lesquelles on peut remplacer la variable pour obtenir une inégalité vraie. Par exemple :
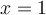 est une des solutions de l'inégalité
est une des solutions de l'inégalité 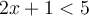 , car en la remplaçant dans cette dernière on obtient
, car en la remplaçant dans cette dernière on obtient 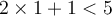 qui est une inégalité vraie.
qui est une inégalité vraie. Par contre
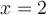 n'est pas une solution, car
n'est pas une solution, car 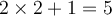 et
et 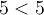 est une inégalité fausse.
est une inégalité fausse. On voit que les solutions de cette inéquation sont toutes les valeurs telles que
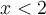 .
.Afin de résoudre une inéquation, il faut la transformer en une ou plusieurs inéquations équivalentes de la forme :
Pour y arriver, on peut bien sûr utiliser les opérations élémentaires  et
et 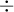 . Par contre, pour chacune des opérations il faut respecter certaines propriétés.
. Par contre, pour chacune des opérations il faut respecter certaines propriétés.
Exemples :
a) Trouvons l'ensemble solution de l'inéquation 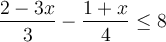
L'ensemble solution de cette inéquation est décrit par
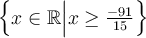 ou par l'intervalle
ou par l'intervalle 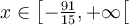 .
.
b) Trouvons le domaine de l'équation 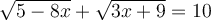
On cherche l'ensemble des valeurs de  pour lesquelles chacune des expressions existe dans
pour lesquelles chacune des expressions existe dans 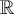 .
.
Puisque la racine carrée d'un nombre négatif n'est pas définie, il faut que
Le domaine est donc l'ensemble des valeurs pour lesquelles  et
et 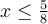 , ce qui correspond à l'intervalle
, ce qui correspond à l'intervalle ![\left[{-3, \frac{5}{8}}\right] \left[{-3, \frac{5}{8}}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/18304db4caf8272aa1b28c91c58d2a2d.png) .
.
Exercices formatifs WeBWorK
 Résoudre des inéquations
Résoudre des inéquations
2. Résoudre une inéquation à l'aide d'un tableau de signes
Soit une inéquation qui peut être exprimée sous la forme suivante :
où 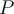 et
et 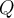 sont des polynômes factorisables, c'est-à-dire que l'on peut exprimer comme un produit ou un quotient de plusieurs facteurs. Comme le signe de l'expression dépend du signe de chacun des facteurs, il est utile de résoudre l'inéquation à l'aide d'un tableau de signes pour s'assurer d'inclure tous les cas possibles.
sont des polynômes factorisables, c'est-à-dire que l'on peut exprimer comme un produit ou un quotient de plusieurs facteurs. Comme le signe de l'expression dépend du signe de chacun des facteurs, il est utile de résoudre l'inéquation à l'aide d'un tableau de signes pour s'assurer d'inclure tous les cas possibles.
Il suffit de suivre la règle des signes pour la multiplication et la division. Comme que le nombre  sépare les nombres négatifs des nombres positifs, il faudra trouver les zéros de chacun des facteurs afin de construire le tableau de signes.
sépare les nombres négatifs des nombres positifs, il faudra trouver les zéros de chacun des facteurs afin de construire le tableau de signes.
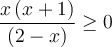 .
.
- On trouve les zéros des trois facteurs
 ,
, 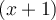 et
et 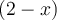 , soit
, soit 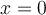 ,
, 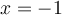 et
et 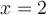 :
: - On construit le tableau de signes en suivant ces étapes :
- La première ligne représente le domaine de l'expression.
- On insère une colonne pour chacun des zéros des facteurs en les plaçant dans l'ordre croissant.
- On insère ensuite une colonne pour représenter les intervalles contenant les nombres réels avant, entre et après les zéros.
- On construit une ligne pour chacun des facteurs.
- La dernière ligne est attribuée à l'expression globale.
![\left]{-\infty,-1}\right[ \left]{-\infty,-1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/74e3fe43014de035aed99ecf1bf8300f.png)
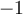
![\left]{-1,0}\right[ \left]{-1,0}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cac34ed84b1a413c0f8a79e51dc83669.png)

![\left]{0,2}\right[ \left]{0,2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d1f6239d39a919dea9c5ce06689b3b86.png)
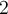
![\left]{2,\infty}\right[ \left]{2,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/050db329384ac4505ba45f1d048eb32c.png)

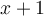
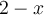
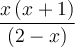
- Pour chacune des lignes des facteurs, on inscrit le nombre
 dans la colonne correspondante à son zéro.
dans la colonne correspondante à son zéro.
![\left]{-\infty,-1}\right[ \left]{-\infty,-1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/74e3fe43014de035aed99ecf1bf8300f.png)
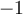
![\left]{-1,0}\right[ \left]{-1,0}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cac34ed84b1a413c0f8a79e51dc83669.png)

![\left]{0,2}\right[ \left]{0,2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d1f6239d39a919dea9c5ce06689b3b86.png)
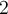
![\left]{2,\infty}\right[ \left]{2,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/050db329384ac4505ba45f1d048eb32c.png)


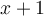

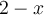

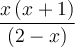
- On détermine le signe de chaque facteur en résolvant les inéquations appropriées. On reporte ensuite les résultats sur la ligne réservée de chaque facteur en y inscrivant le symbole
 ou
ou  dans les cases correspondant aux intervalles lorsque le facteur prend une valeur positive ou négative.
dans les cases correspondant aux intervalles lorsque le facteur prend une valeur positive ou négative.
![\left]{-\infty,-1}\right[ \left]{-\infty,-1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/74e3fe43014de035aed99ecf1bf8300f.png)
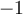
![\left]{-1,0}\right[ \left]{-1,0}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cac34ed84b1a413c0f8a79e51dc83669.png)

![\left]{0,2}\right[ \left]{0,2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d1f6239d39a919dea9c5ce06689b3b86.png)
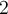
![\left]{2,\infty}\right[ \left]{2,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/050db329384ac4505ba45f1d048eb32c.png)








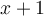







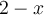







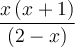
- On remplit la dernière ligne du tableau en
 indiquant pour chaque intervalle :
indiquant pour chaque intervalle :
- le nombre
 si le produit et quotient des facteurs est nul;
si le produit et quotient des facteurs est nul; - le symbole
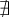 si la valeur de
si la valeur de  n'appartient pas au domaine;
n'appartient pas au domaine; - le signe du produit et quotient des facteurs en respectant la règle des signes.
![\left]{-\infty,-1}\right[ \left]{-\infty,-1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/74e3fe43014de035aed99ecf1bf8300f.png)
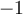
![\left]{-1,0}\right[ \left]{-1,0}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cac34ed84b1a413c0f8a79e51dc83669.png)

![\left]{0,2}\right[ \left]{0,2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d1f6239d39a919dea9c5ce06689b3b86.png)
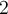
![\left]{2,\infty}\right[ \left]{2,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/050db329384ac4505ba45f1d048eb32c.png)








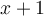







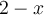







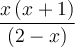





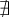

- le nombre
- On peut maintenant interpréter le tableau de signes afin de résoudre l'inéquation de départ. On a que
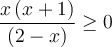 pour les valeurs de
pour les valeurs de  pour lesquelles on a inscrit le signe
pour lesquelles on a inscrit le signe  ou le nombre
ou le nombre  .
.
Autres exemples :
Exercices formatifs WeBWorK
 Résoudre une inéquation à l'aide d'un tableau de signes
Résoudre une inéquation à l'aide d'un tableau de signes
3. Résoudre une inéquation contenant des valeurs absolues
Nous pouvons séparer en deux cas les inéquations contenant une valeur absolue pour bien comprendre comment les résoudre.
- Si
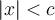 (ou
(ou 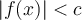 )
)
Les valeurs de
 qui vérifient cette inéquation appartiennent à l'intervalle
qui vérifient cette inéquation appartiennent à l'intervalle ![\left[{-c, c}\right] \left[{-c, c}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f7052b8b0777d8a957d26db66dda4e0c.png) . Il faut donc que
. Il faut donc que 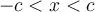 , c'est-à-dire que
, c'est-à-dire que  soit à la fois supérieur à
soit à la fois supérieur à 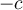 et inférieur à
et inférieur à 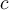 .
.Notre démarche consiste donc à chercher des solutions communes aux deux inéquations :
- Si
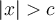 (ou
(ou 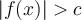 )
)
Les valeurs de
 qui vérifient cette inéquation appartiennent aux intervalles
qui vérifient cette inéquation appartiennent aux intervalles ![\left]{-\infty,-c}\right] \left]{-\infty,-c}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9092c823218dd70d62c18280c65a5ac1.png) ou
ou 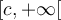 , c'est-à-dire que
, c'est-à-dire que  peut être inférieur à
peut être inférieur à 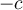 ou bien supérieur à
ou bien supérieur à 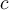 .
.Notre démarche consiste donc à faire l'union des ensembles solutions de ces deux inéquations :
Exemples :
a) Trouvons l'ensemble solution de l'inéquation 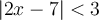 .
.
Il faut trouver les valeurs de  telles que l'expression à l'intérieur de la valeur absolue est à la fois inférieure à
telles que l'expression à l'intérieur de la valeur absolue est à la fois inférieure à 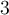 et supérieure à
et supérieure à 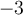 , c'est-à-dire
, c'est-à-dire 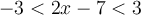 .
.
Il faut résoudre les deux inéquations suivantes et à faire l'intersection des deux ensembles solutions.
Aidons nous du graphique Geogebra ci-dessous pour comprendre la solution de cette inéquation. ![]() En déplaçant le point vert sur la droite, on peut voir le résultat de la valeur absolue
En déplaçant le point vert sur la droite, on peut voir le résultat de la valeur absolue 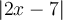 pour certaines valeurs de
pour certaines valeurs de  . L'ensemble solution contient toutes les valeurs de
. L'ensemble solution contient toutes les valeurs de  qui sont à la fois inférieures à
qui sont à la fois inférieures à 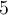 et supérieures à
et supérieures à 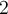 , c'est-à-dire les valeurs de
, c'est-à-dire les valeurs de  qui appartiennent à l'intervalle
qui appartiennent à l'intervalle ![\left]2,5\right[, \left]2,5\right[,](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/bcc62aaa4e24d29008d1ad343249bfb8.png) comme le montre la trace en bleue sur l'axe des
comme le montre la trace en bleue sur l'axe des  .
.
De plus, on remarque que pour 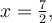 l'intérieur de la valeur absolue est nul, car
l'intérieur de la valeur absolue est nul, car 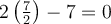 . Ainsi, lorsque
. Ainsi, lorsque  l'intérieur de la valeur absolue devient négatif, soit
l'intérieur de la valeur absolue devient négatif, soit 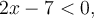 et lorsque
et lorsque 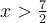 , l'intérieur devient positif, soit
, l'intérieur devient positif, soit 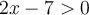 . Cela correspond bien à la définition de la valeur absolue :
. Cela correspond bien à la définition de la valeur absolue :
b) Trouvons l'ensemble solution de l'inéquation 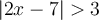 .
.
Il faut trouver les valeurs de  qui appartiennent à l'un ou l'autre des ensembles solutions des deux inéquations :
qui appartiennent à l'un ou l'autre des ensembles solutions des deux inéquations :
Il faut faire l'union de ces deux ensembles que l'on a représentés sur l'axe réel suivant :

Les valeurs de  peuvent donc appartenir à l'intervalle
peuvent donc appartenir à l'intervalle ![\left]-\infty, 2\right[ \left]-\infty, 2\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/985af0e347708f0b302c0374c1e44f50.png) ou bien à l'intervalle
ou bien à l'intervalle ![\left]{5, +\infty}\right[ \left]{5, +\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f96c4f335e3d8de6db3ca39e7b6bbcbd.png) .
.
L'ensemble solution de l'inéquation 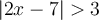 est donc
est donc ![\Bigl]{-\infty, 2}\Bigr[ \cup \Bigl]{5, +\infty}\Bigr[ \Bigl]{-\infty, 2}\Bigr[ \cup \Bigl]{5, +\infty}\Bigr[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f7b08192686b439561617325958f062c.png) .
.
c) Trouvons l'ensemble solution de l'inéquation 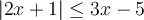 .
.
Il faut trouver les valeurs de  qui sont communes aux ensembles solutions des deux inéquations :
qui sont communes aux ensembles solutions des deux inéquations :
Il faut faire l'intersection de ces deux ensembles que l'on a représentés sur l'axe réel suivant :

C'est-à-dire que les valeurs de  appartiennent à la fois à l'intervalle
appartiennent à la fois à l'intervalle 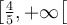 et à l'intervalle
et à l'intervalle 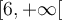 .
.
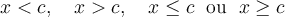
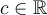
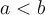
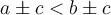
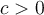
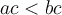
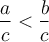
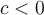
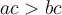
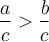
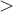
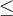
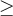
![\begin{array}{rcll} \dfrac{4\left({2-3x}\right) - 3\left({1+x}\right)}{12} & \leq & 8 & \small\text{; dénominateur commun} \\[1em]\dfrac{5-15x}{12} & \leq & 8 & {} \\[1em]5 - 15x & \leq & \pmb{12} \times 8 & \small\text{; on a multiplié par }12 \text{ chaque membre sans changer le sens de l'inégalité} \\[0.8em]-15x & \leq & 96 - \pmb{5} & \small\text{; on a soustrait }5 \text{ à chaque membre sans changer le sens de l'inégalité} \\[0.8em]x & \geq & \dfrac{91}{\pmb{-15}} & \small\text{; on a divisé par }-15 \text{ chaque membre }\textbf{en changeant le sens de l'inégalité} \end{array} \begin{array}{rcll} \dfrac{4\left({2-3x}\right) - 3\left({1+x}\right)}{12} & \leq & 8 & \small\text{; dénominateur commun} \\[1em]\dfrac{5-15x}{12} & \leq & 8 & {} \\[1em]5 - 15x & \leq & \pmb{12} \times 8 & \small\text{; on a multiplié par }12 \text{ chaque membre sans changer le sens de l'inégalité} \\[0.8em]-15x & \leq & 96 - \pmb{5} & \small\text{; on a soustrait }5 \text{ à chaque membre sans changer le sens de l'inégalité} \\[0.8em]x & \geq & \dfrac{91}{\pmb{-15}} & \small\text{; on a divisé par }-15 \text{ chaque membre }\textbf{en changeant le sens de l'inégalité} \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8bd54b5f1c3059ef520721fe769e20a1.png)
![\begin{array}{rclcrcl} 5-8x & \geq & 0 &\quad\text{ et }\quad& 3x+9 & \geq & 0 \\[0.8em]-8x & \geq & -5 & {} & 3x & \geq & -9 \\[0.8em]x & \mathbf{\leq} & \dfrac{5}{8} & {} & x & \geq & -3 \end{array} \begin{array}{rclcrcl} 5-8x & \geq & 0 &\quad\text{ et }\quad& 3x+9 & \geq & 0 \\[0.8em]-8x & \geq & -5 & {} & 3x & \geq & -9 \\[0.8em]x & \mathbf{\leq} & \dfrac{5}{8} & {} & x & \geq & -3 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f11aa3eafe1c6aa2fb7fd389052e9401.png)
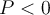
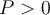
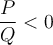
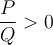
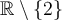
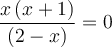
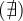
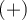
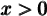
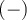
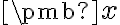
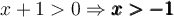
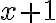
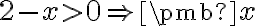
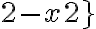
![\boxed{\left]{-\infty,-1}\right] \cup \left[{0,2}\right[} \boxed{\left]{-\infty,-1}\right] \cup \left[{0,2}\right[}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c54fc63cb13eaaab0e349a970f991815.png)