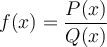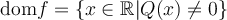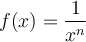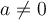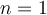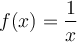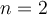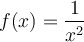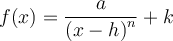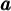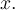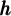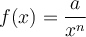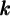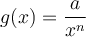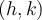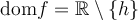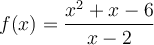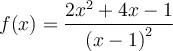2.2 Les fonctions algébriques
- Fonction linéaire (droite)
- Fonction quadratique (parabole)
- Fonction puissance (exposant naturel)
- Fonction rationnelle
- Fonction racine et exposant fractionnaire
- Trouver le domaine d'une fonction algébrique
4. Fonction rationnelle
Tout comme les fonctions puissances, les graphiques des fonctions rationnelles peuvent prendre différentes formes selon les degrés des polynômes. Tracer le graphique de telles fonctions peut s'avérer complexe. Le cours de Calcul différentiel nous permettra d'analyser plusieurs caractéristiques de ces courbes dont les intervalles de croissance et de décroissance, les extremums et le sens de la concavité.
À partir du graphique GeoGebra suivant, nous allons tout d'abord étudier en détails les caractéristiques des fonctions rationnelles de base de la forme
![]() Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique de l'augmentation ou de la diminution de l'exposant. Les premières valeurs de
Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique de l'augmentation ou de la diminution de l'exposant. Les premières valeurs de  correspondent aux fonctions suivantes :
correspondent aux fonctions suivantes :
Voici quelques caractéristiques communes de ces fonctions.
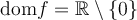 .
.- Toutes ces fonctions ont comme asymptote verticale
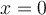 et comme asymptote horizontale
et comme asymptote horizontale 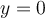 . Le centre du graphique est le point d'intersection des deux asymptotes, soit le point
. Le centre du graphique est le point d'intersection des deux asymptotes, soit le point 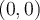 .
. - Elles n'ont aucun zéro ni ordonnée à l'origine.
- Elles possèdent aucun minimum ni maximum.
On peut également créer d'autres fonctions composées à partir des fonctions rationnelles de base. Nous élaborerons ce concept plus en détail dans la section sur les transformations de fonctions. Pour l'instant, dans le graphique Geogebra, on s'intéresse aux fonctions de la forme
![]() Déplacez les différents curseurs « a », « h » et « k ».
Déplacez les différents curseurs « a », « h » et « k ».
![]() Ex. : Choisissez la fonction de base
Ex. : Choisissez la fonction de base 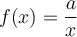 . Si
. Si 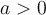 , la fonction est décroissante sur son domaine et est positive sur l'intervalle
, la fonction est décroissante sur son domaine et est positive sur l'intervalle ![\left]{0, \infty}\right[ \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d13a6e4c304d2f4a427dad83ef19750a.png) . Si
. Si 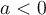 , la fonction est croissante sur son domaine et est positive sur l'intervalle
, la fonction est croissante sur son domaine et est positive sur l'intervalle ![\left]{-\infty, 0}\right[ \left]{-\infty, 0}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/da7e2fe2d02a9ece3c4691a384fe1f74.png) .
.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 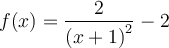 . On remarque que tous les points du graphique de base
. On remarque que tous les points du graphique de base 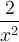 subissent un déplacement vers la gauche de
subissent un déplacement vers la gauche de  et vers le bas de
et vers le bas de 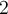 . Le centre
. Le centre 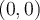 se déplace donc au point
se déplace donc au point 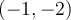 . Ainsi,
. Ainsi, 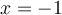 est l'asymptote verticale et
est l'asymptote verticale et 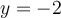 est l'asymptote horizontale.
est l'asymptote horizontale.
Par conséquent, on peut généraliser les résultats précédents.
Nous nous intéressons également au domaine des fonctions rationnelles. Les sections sur la simplification de fractions rationnelles et sur la résolution d'équations contenant des fractions rationnelles nous aideront particulièrement.
Voici quelques exemples de fonctions intéressantes, ainsi que leur représentation graphique.