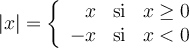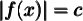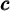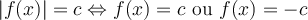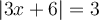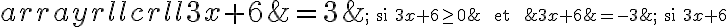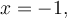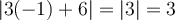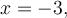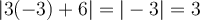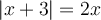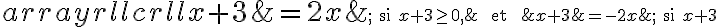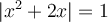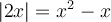1.4 Les équations
- Définitions
- Principes pour résoudre des équations
- Équations contenant des fractions rationnelles
- Équations contenant des racines carrées
- Équations contenant des valeurs absolues
5. Équations contenant des valeurs absolues
La valeur absolue d'un nombre  donne toujours un résultat positif. Par exemple,
donne toujours un résultat positif. Par exemple, 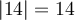 et
et 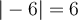 . Par définition, la fonction
. Par définition, la fonction 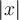 laisse positif tout nombre
laisse positif tout nombre  qui est déjà positif et rend positif tout nombre
qui est déjà positif et rend positif tout nombre  qui est négatif. On peut aussi la définir de la façon suivante :
qui est négatif. On peut aussi la définir de la façon suivante :
Cette façon de définir la valeur absolue est équivalente. En effet, dans les deux cas on obtient 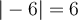 et
et 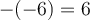 comme le montre le graphique Geogebra suivant.
comme le montre le graphique Geogebra suivant. ![]() Déplacez le point vert
Déplacez le point vert![]() sur la droite des réels et remarquez la définition de la valeur absolue selon que le nombre
sur la droite des réels et remarquez la définition de la valeur absolue selon que le nombre  est positif ou négatif.
est positif ou négatif.
Pour résoudre une équation contenant des valeurs absolues, on doit considérer deux cas possibles : si l'expression à l'intérieur est positive et si elle est négative.
La résolution des formes d'équations suivantes respecte ce principe.
Résolution d'une équation de la forme 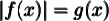
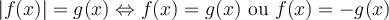
- On vérifie les solutions dans l'équation initiale et on rejette celles qui ne vérifient pas l'équation.
Comme le membre de droite n'est pas une constante mais contient une variable  , la valeur du membre de droite peut donc devenir négative, ce qui est interdit. Par conséquent, il est essentiel de vérifier si les solutions transforment l'équation en une égalité vraie.
, la valeur du membre de droite peut donc devenir négative, ce qui est interdit. Par conséquent, il est essentiel de vérifier si les solutions transforment l'équation en une égalité vraie.
Exemples : Résoudre les équations suivantes.
Selon la définition de la valeur absolue, résoudre cette équation revient à résoudre les deux équations suivantes :
Les deux solutions de cette équation sont  et
et  . On peut même le vérifier en remplaçant ces deux valeurs dans l'équation de départ.
. On peut même le vérifier en remplaçant ces deux valeurs dans l'équation de départ.
Étant donné que 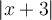 est toujours positif, il faut aussi que
est toujours positif, il faut aussi que 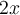 soit toujours positif. Ainsi, on a comme restriction :
soit toujours positif. Ainsi, on a comme restriction : 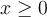 . On peut maintenant résoudre les deux équations suivantes :
. On peut maintenant résoudre les deux équations suivantes :
Or 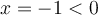 et par conséquent ne respecte pas la restriction. En effet, en remplaçant
et par conséquent ne respecte pas la restriction. En effet, en remplaçant 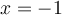 dans l'équation initiale, on obtient
dans l'équation initiale, on obtient
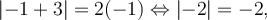 ce qui est faux. Par conséquent,
ce qui est faux. Par conséquent, 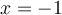 n'est pas une solution et
n'est pas une solution et  est la seule solution de l'équation.
est la seule solution de l'équation.
Exemples : Résoudre les équations suivantes.