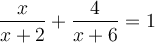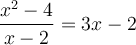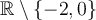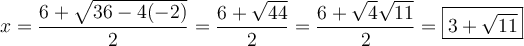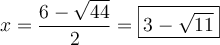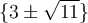Précédent
Suivant

3. Équations contenant des fractions rationnelles

Lorsqu'une équation contient des fractions rationnelles, il faut d'abord bien déterminer le domaine.

Après avoir résolu l'équation, on doit vérifier si les solutions trouvées font partie du domaine.

Exemple : Résoudre l'équation 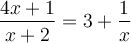\dfrac{4x+1}{x+2} = 3+\dfrac{1}{x}.

Le domaine est \mathbb{R} \setminus \lbrace -2,0 \rbrace.

Résolution :

\begin{array}{rll}\Rightarrow\dfrac{4x+1}{x+2}&=\dfrac{3x+1}{x}&\\\Rightarrow\dfrac{4x+1}{x+2}\cdot\pmb{x(x+2)}&=\dfrac{3x+1}{x}\cdot\pmb{x(x+2)}&\small{\text{; si }x\neq 0\text{ on peut multiplier par }x}\\&&\small{\text{ et si } x \neq -2 \text{ on peut multiplier par } x+2}\\ \Rightarrow (4x+1)\cdot x &= (3x+1)(x+2)&\\ \Rightarrow 4x^2+x &=3x^2+7x+2 &\\ \Rightarrow 4x^2-3x^2+x-7x-2&= 0 & \small\text{; on transforme en une équation quadratique}\\ \Rightarrow x^2-6x-2 &= 0 & \end{array}

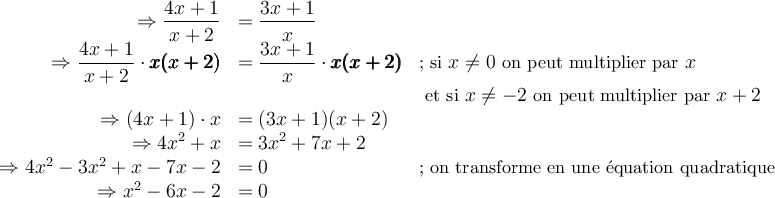
On peut peut utiliser la formule quadratique 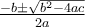\frac{-b \pm \sqrt{{b^2}-4ac}}{2a} pour résoudre x^2-6x-2=0.

x = \dfrac{6 + \sqrt{36-4(-2)}}{2} = \dfrac{6+\sqrt{44}}{2} = \dfrac{6+\sqrt{4}\sqrt{11}}{2}=\boxed{3+\sqrt{11}}

et x = \dfrac{6 - \sqrt{44}}{2} =\boxed{3 - \sqrt{11}}

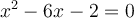Ces deux valeurs appartiennent au domaine et vérifient l'équation initiale.

L'ensemble solution est donc \lbrace 3 \pm \sqrt{11} \rbrace.

Exemples : Résoudre les équations suivantes.

  • Exemple 2 : \dfrac{x}{x+2} + \dfrac{4}{x+6} = 1
  • Exemple 3 : \dfrac{{x^2} - 4}{x-2} = 3x-2

    • Exercices formatifs WeBWorK

    logo WeBWorK Résoudre des équations linéaires, quadratiques et rationnelles
    Précédent
    Suivant