1.3 Les fractions rationnelles
- Introduction
- Simplification de fractions rationnelles
- Opérations sur les fractions rationnelles
- Simplification de fractions complexes
3. Opérations sur les fractions rationnelles
 L'addition et la soustraction
L'addition et la soustraction
Pour additionner ou soustraire des fractions rationnelles, il faut :
- Transformer chacune des fractions sur un dénominateur commun.
- Additionner (ou soustraire) les numérateurs et diviser par le dénominateur commun.
- Simplifier la fraction, si possible.
Exemple : Effectuons l'addition suivante : 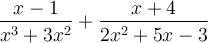 .
.
On factorise tout d'abord les dénominateurs afin de trouver un dénominateur commun :
Le domaine de cette fraction est donc : 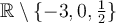 .
.
 La multiplication et la division
La multiplication et la division
Exemple : Effectuons la multiplication suivante : 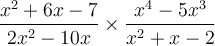 .
.
Il faut factoriser et multiplier les numérateurs et les dénominateurs des deux fractions. La factorisation permet de simplifier plus facilement.
On a pu diviser par les facteurs communs  ,
, 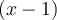 et
et 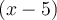 , car le domaine de cette fraction est :
, car le domaine de cette fraction est : 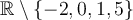 où
où 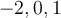 et
et 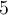 sont les valeurs de
sont les valeurs de  pour lesquelles les dénominateurs
pour lesquelles les dénominateurs 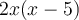 et
et 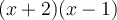 sont nuls.
sont nuls.
Exemples : Effectuons les opérations suivantes.
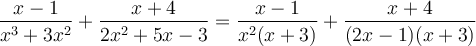
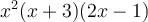
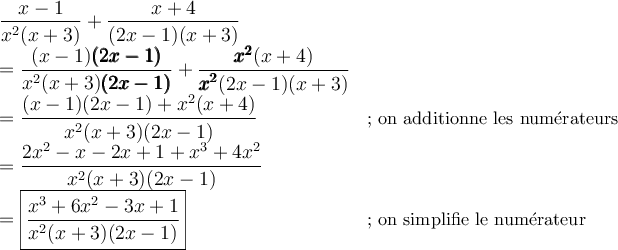
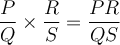
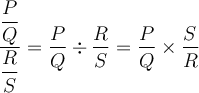
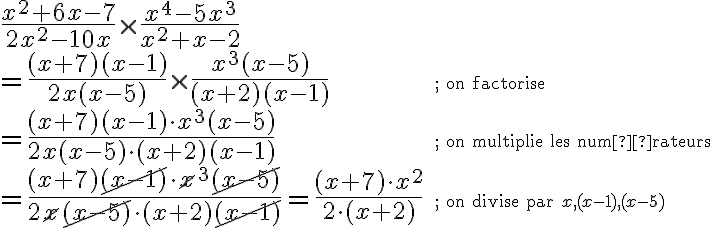
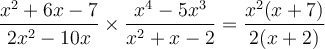
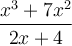
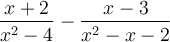
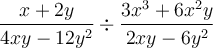
 Simplification et opérations sur les fractions rationnelles
Simplification et opérations sur les fractions rationnelles