1.3 Les fractions rationnelles
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 1.3 Les fractions rationnelles |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 09:05 |
Description
- Introduction
- Simplification de fractions rationnelles
- Opérations sur les fractions rationnelles
- Simplification de fractions complexes
1. Introduction
On appelle fraction rationnelle toute expression de la forme 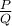 , où
, où 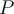 et
et 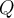 sont des polynômes et
sont des polynômes et 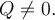
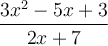 est une fraction rationnelle.
est une fraction rationnelle.
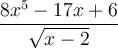 n'est pas une fraction rationnelle, car son dénominateur n'est pas un polynôme.
n'est pas une fraction rationnelle, car son dénominateur n'est pas un polynôme.
Le domaine d'une fraction rationnelle est l'ensemble de toutes les valeurs réelles 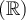 telles que le dénominateur est
telles que le dénominateur est 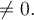
2. Simplification de fractions rationnelles
Simplifier une fraction signifie diviser le numérateur et le dénominateur par un même facteur. Il faut donc exprimer le numérateur et le dénominateur sous la forme d'un produit afin de permettre cette simplification.
Pour simplifier une fraction rationnelle, il faut :
- Factoriser son numérateur et son dénominateur.
- Trouver son domaine.
- Déterminer les facteurs communs au numérateur et au dénominateur.
- Diviser le numérateur et le dénominateur par ces facteurs communs.
Exemples : Simplifions la fraction 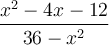 .
.
On factorise le numérateur et le dénominateur :
On remarque que les facteurs 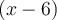 et
et 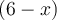 sont opposés :
sont opposés : 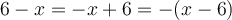
On peut diviser le numérateur et le dénominateur par le facteur commun 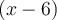 . Cette division est possible, car
. Cette division est possible, car 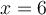 n'appartient pas au domaine,
n'appartient pas au domaine, 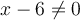 .
.
Exemples : Simplifions, si possible, les fractions suivantes.
3. Opérations sur les fractions rationnelles
 L'addition et la soustraction
L'addition et la soustraction
Pour additionner ou soustraire des fractions rationnelles, il faut :
- Transformer chacune des fractions sur un dénominateur commun.
- Additionner (ou soustraire) les numérateurs et diviser par le dénominateur commun.
- Simplifier la fraction, si possible.
Exemple : Effectuons l'addition suivante : 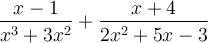 .
.
On factorise tout d'abord les dénominateurs afin de trouver un dénominateur commun :
Le domaine de cette fraction est donc : 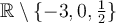 .
.
 La multiplication et la division
La multiplication et la division
Exemple : Effectuons la multiplication suivante : 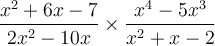 .
.
Il faut factoriser et multiplier les numérateurs et les dénominateurs des deux fractions. La factorisation permet de simplifier plus facilement.
On a pu diviser par les facteurs communs  ,
, 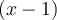 et
et 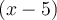 , car le domaine de cette fraction est :
, car le domaine de cette fraction est : 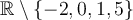 où
où 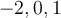 et
et 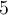 sont les valeurs de
sont les valeurs de  pour lesquelles les dénominateurs
pour lesquelles les dénominateurs 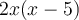 et
et 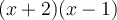 sont nuls.
sont nuls.
Exemples : Effectuons les opérations suivantes.
Exercices formatifs WeBWorK
 Simplification et opérations sur les fractions rationnelles
Simplification et opérations sur les fractions rationnelles
4. Simplification de fractions complexes
On appelle une fraction rationnelle complexe une fraction à «plusieurs étages». Afin de simplifier ce type de fraction, il faut :
- Respecter l'ordre de priorités des opérations.
- Ne pas oublier qu'il y a toujours une parenthèse autour du dénominateur dans une
fraction :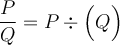
Exemple : Simplifions la fraction complexe suivante : 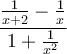 .
.
On peut réécrire cette expression comme
L'ordre de priorité des opérations nous oblige à effectuer tout d'abord l'intérieur des parenthèses 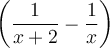 et
et 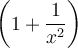 . En mettant les deux expressions sur un dénominateur commun, on obtient :
. En mettant les deux expressions sur un dénominateur commun, on obtient :
On a effectué la division en multipliant la première fraction par l'inverse de la deuxième. Il ne reste qu'à simplifier la fraction en divisant par  , où
, où 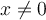 .
.
Exemple : Simplifions la fraction complexe suivante.
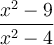
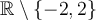

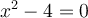
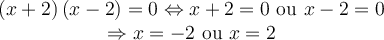
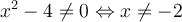
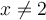
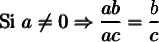
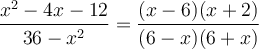
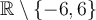
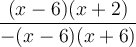
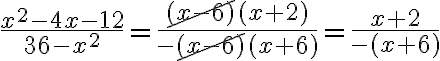
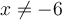
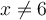
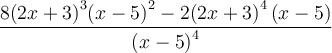
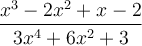
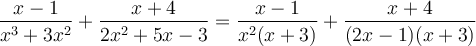
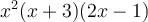
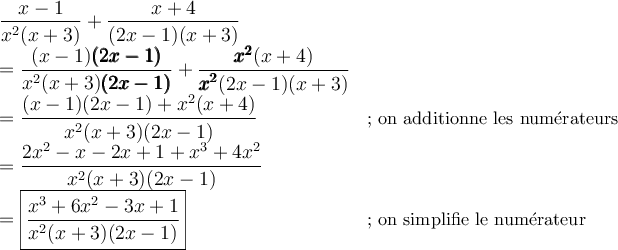
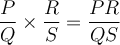
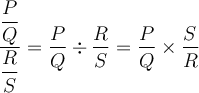
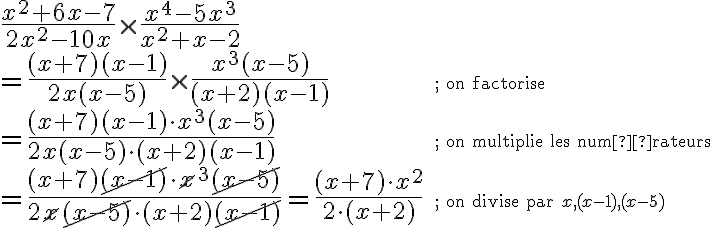
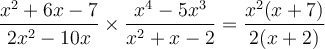
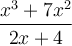
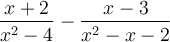
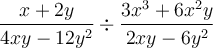
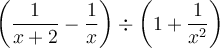
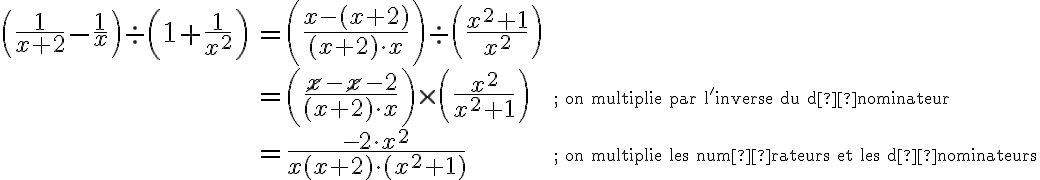
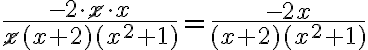
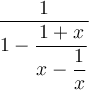
 Simplification de fractions complexes
Simplification de fractions complexes