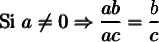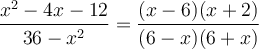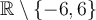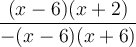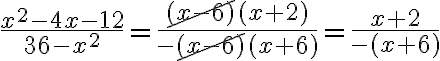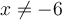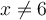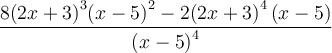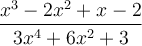1.3 Les fractions rationnelles: Simplification de fractions rationnelles

1.3 Les fractions rationnelles

Introduction
Simplification de fractions rationnelles
Opérations sur les fractions rationnelles
Simplification de fractions complexes

2. Simplification de fractions rationnelles

Simplifier une fraction signifie diviser le numérateur et le dénominateur par un même facteur. Il faut donc exprimer le numérateur et le dénominateur sous la forme d'un produit afin de permettre cette simplification.

$\pmb{ \text{ Si } a \ne 0 \Rightarrow \dfrac{ab}{ac} = \dfrac{b}{c} }$

Pour simplifier une fraction rationnelle, il faut :

Factoriser son numérateur et son dénominateur.
Trouver son domaine.
Déterminer les facteurs communs au numérateur et au dénominateur.
Diviser le numérateur et le dénominateur par ces facteurs communs.

Exemples : Simplifions la fraction 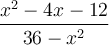$\dfrac{x^2-4x-12}{36 - {x^2}}$ .

On factorise le numérateur et le dénominateur :

$\dfrac{x^2-4x-12}{36-x^2} = \dfrac{(x-6)(x+2)}{(6-x)(6+x)}$

Son domaine est donc : $\mathbb{R}\setminus \lbrace -6,6\rbrace$

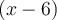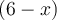On remarque que les facteurs $(x-6)$ et $(6-x)$ sont opposés :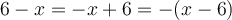 $6-x=-x+6=-(x-6)$

On obtient alors : $\dfrac{(x-6)(x+2)}{-(x-6)(x+6)}$

On peut diviser le numérateur et le dénominateur par le facteur commun 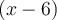$(x-6)$ . Cette division est possible, car 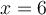$x=6$ n'appartient pas au domaine, $x-6\ne 0$ .

Par conséquent, $\dfrac{x^2-4x-12}{36-x^2}= \dfrac{\cancel{(x-6)}(x+2)}{-\cancel{(x-6)}(x+6)}=\dfrac{x+2}{-(x+6)}$ si $x\ne -6$ et $x\ne 6$ .

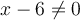Exemples : Simplifions, si possible, les fractions suivantes.