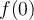2.1 Les fonctions
- Relation et fonction
- Domaine et image
- Graphique d'une fonction
- Points d'intersection avec les axes
4. Points d'intersection avec les axes
Les points d'intersection avec les axes présentent un intérêt particulier pour l'analyse d'une fonction. Ces points sont appelés abcisse à l'origine et ordonnée à l'origine.
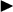 Abcisse à l'origine
Abcisse à l'origine
Les points d'intersection du graphique d'une fonction  avec l'axe horizontal sont tous les points du graphique de la forme
avec l'axe horizontal sont tous les points du graphique de la forme 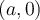 .
.
De plus, la valeur  est un zéro de la fonction
est un zéro de la fonction  , car
, car 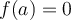 . Ainsi, le nombre de points d'intersection du graphique avec l'axe des
. Ainsi, le nombre de points d'intersection du graphique avec l'axe des  est égal au nombre de zéros de la fonction. On peut en déduire que si une fonction n'a aucun zéro, son graphique ne coupe jamais l'axe horizontal.
est égal au nombre de zéros de la fonction. On peut en déduire que si une fonction n'a aucun zéro, son graphique ne coupe jamais l'axe horizontal.
 est une valeur de
est une valeur de  appartenant au domaine de
appartenant au domaine de  pour laquelle
pour laquelleDe plus, par le théorème de factorisation,
 est un zéro de la fonction
est un zéro de la fonction 

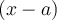 est un facteur de
est un facteur de 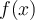 .
.Par conséquent, si une fonction est définie par un produit de facteurs, on peut facilement trouver ses zéros.
Exemple :
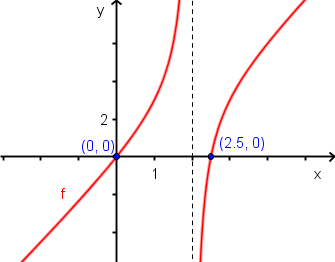
Trouvons, si possible, les zéros de la fonction 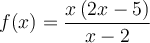 .
.
Pour trouver les zéros de la fonction  , il suffit de trouver les solutions de l'équation
, il suffit de trouver les solutions de l'équation 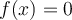 qui appartiennent au domaine.
qui appartiennent au domaine.
Étant donné que ces deux valeurs appartiennent au domaine, la fonction possède deux zéros : 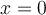 et
et 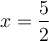 .
.
Les points 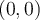 et
et 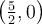 sont donc les points où la courbe croise l'axe des
sont donc les points où la courbe croise l'axe des  .
.
 Ordonnée à l'origine
Ordonnée à l'origine
Ce point d'intersection est unique, car la valeur 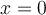 ne peut avoir qu'une seule image par la fonction
ne peut avoir qu'une seule image par la fonction  .
.
Exemple :
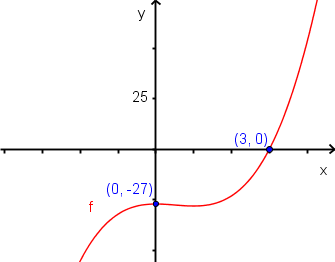
Soit la fonction 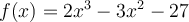 . Trouvons, si possible, tous les zéros de la fonction
. Trouvons, si possible, tous les zéros de la fonction  sachant que le point
sachant que le point 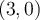 est une abscisse à l'origine.
est une abscisse à l'origine.
Il faut d'abord factoriser le polynôme 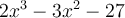 afin de résoudre l'équation
afin de résoudre l'équation 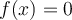 .
.
Étant donné que 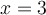 est une solution de l'équation, alors par le théorème de factorisation,
est une solution de l'équation, alors par le théorème de factorisation, 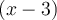 est un facteur de
est un facteur de 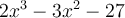 . Nous obtenons donc que
. Nous obtenons donc que
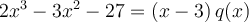 , où
, où 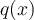 est un polynôme de degré
est un polynôme de degré 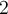 .
.
Nous pouvons trouver le polynôme 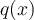 en effectuant la division suivante:
en effectuant la division suivante:
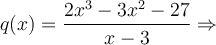 |
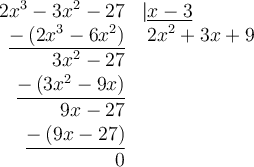 |
On peut donc écrire 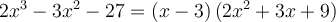 .
.
Or, le polynôme 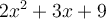 est non factorisable, car son discriminant
est non factorisable, car son discriminant 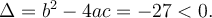
Alors 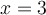 est la seule solution de l'équation
est la seule solution de l'équation 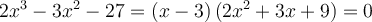 .
.
Donc la fonction 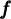 possède comme seul zéro
possède comme seul zéro 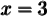 .
.
De plus, l'ordonnée à l'origine est 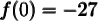 . Ainsi, le graphique coupe l'axe des
. Ainsi, le graphique coupe l'axe des  au point
au point 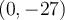 .
.
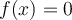
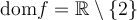
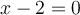
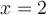
![\begin{array}{lcl} \dfrac{x\left({2x-5}\right)}{x-2} =0 & \Leftrightarrow & x\left({2x-5}\right)=0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } 2x-5 = 0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } x = \frac{5}{2} \end{array} \begin{array}{lcl} \dfrac{x\left({2x-5}\right)}{x-2} =0 & \Leftrightarrow & x\left({2x-5}\right)=0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } 2x-5 = 0 \\[0.8em] & \Leftrightarrow & x =0 \text{ ou } x = \frac{5}{2} \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6aa5aff29220bfa7b9ebef9c1d3632e6.png)