1.3 Les fractions rationnelles
- Introduction
- Simplification de fractions rationnelles
- Opérations sur les fractions rationnelles
- Simplification de fractions complexes
4. Simplification de fractions complexes
On appelle une fraction rationnelle complexe une fraction à «plusieurs étages». Afin de simplifier ce type de fraction, il faut :
- Respecter l'ordre de priorités des opérations.
- Ne pas oublier qu'il y a toujours une parenthèse autour du dénominateur dans une
fraction :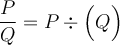
Exemple : Simplifions la fraction complexe suivante : 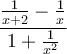 .
.
On peut réécrire cette expression comme
L'ordre de priorité des opérations nous oblige à effectuer tout d'abord l'intérieur des parenthèses 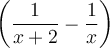 et
et 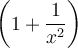 . En mettant les deux expressions sur un dénominateur commun, on obtient :
. En mettant les deux expressions sur un dénominateur commun, on obtient :
On a effectué la division en multipliant la première fraction par l'inverse de la deuxième. Il ne reste qu'à simplifier la fraction en divisant par  , où
, où 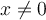 .
.
Exemple : Simplifions la fraction complexe suivante.
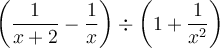
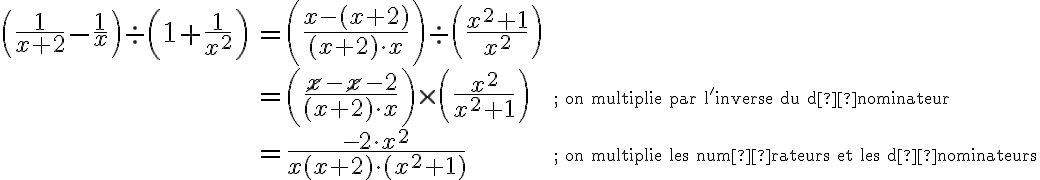
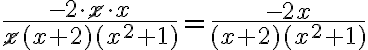
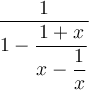
 Simplification de fractions complexes
Simplification de fractions complexes