1.1 Les polynômes et les racines
- Définitions
- Opérations sur les polynômes
- Racines et exposants fractionnaires
3. Racines et exposants fractionnaires
Par exemple :
Racines paires
Pour calculer la racine n-ième paire d'un nombre  , il faut respecter ces deux règles :
, il faut respecter ces deux règles :
- Le nombre
 ne doit pas être négatif, c'est-à-dire que
ne doit pas être négatif, c'est-à-dire que 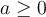 .
. - Le nombre
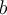 , qui est la racine n-ième de
, qui est la racine n-ième de  , ne doit pas être négatif non plus.
, ne doit pas être négatif non plus.
En effet, si  , alors
, alors ![\sqrt[n]{a} \sqrt[n]{a}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.png) n'existe pas pour les entiers
n'existe pas pour les entiers  pairs. Par exemple,
pairs. Par exemple,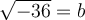 n'existe pas, car il n'existe aucun nombre réel
n'existe pas, car il n'existe aucun nombre réel 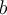 tel que
tel que 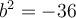 .
.
De plus, même si 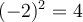 et que
et que 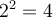 , on dira que
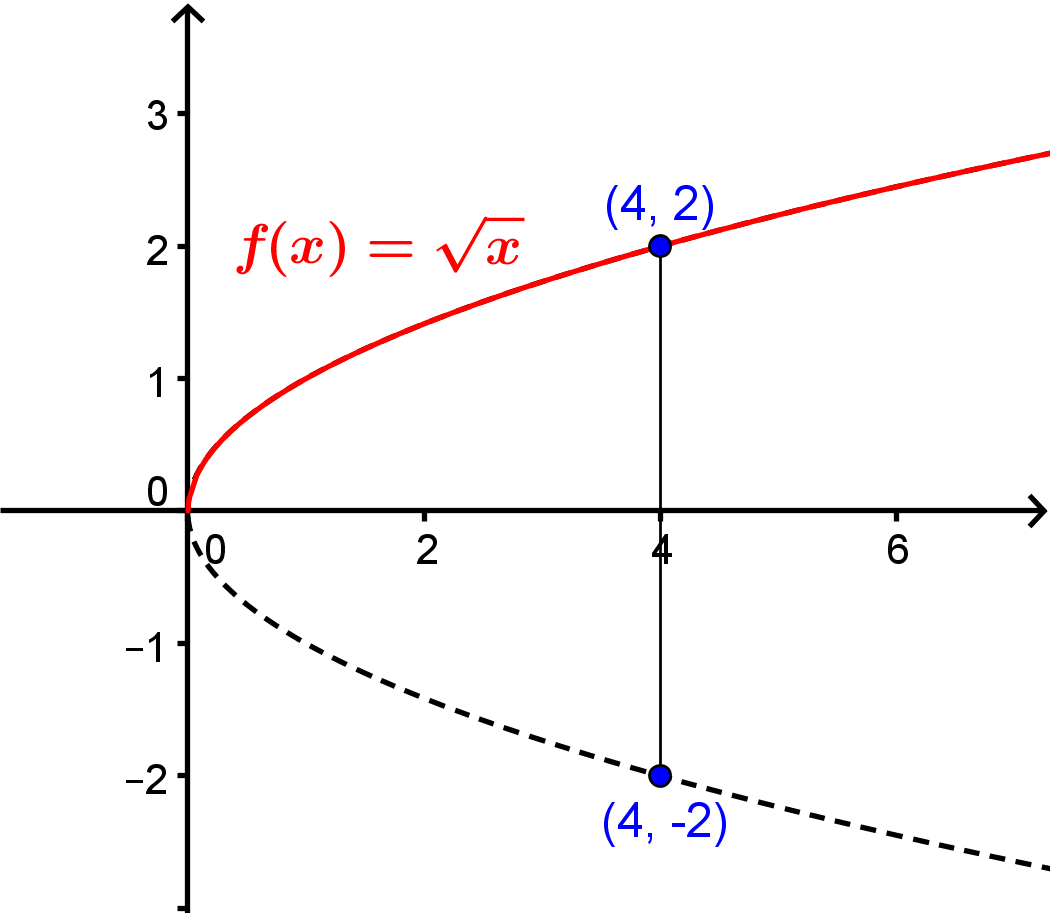
, on dira que 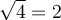 , soit la racine positive de 4. Il ne faut jamais écrire
, soit la racine positive de 4. Il ne faut jamais écrire 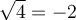 , car la racine carrée doit être une fonction par définition, c'est-à-dire qu'à toute valeur de
, car la racine carrée doit être une fonction par définition, c'est-à-dire qu'à toute valeur de  doit correspondre une seule image
doit correspondre une seule image 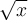 . Cette notion est expliquée plus en détails dans la section sur les fonctions, mais la figure ci-contre illustre bien ce cas.
. Cette notion est expliquée plus en détails dans la section sur les fonctions, mais la figure ci-contre illustre bien ce cas.
Racines impaires
Contrairement à la racine paire, la racine n-ième impaire d'un nombre  est toujours définie. Dans ce cas, on a
est toujours définie. Dans ce cas, on a
Par exemple, on aura ![\sqrt[3]{8} = 2 \sqrt[3]{8} = 2](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/aae2ac845a729da53b6a3a79cc4458ae.png) , car
, car 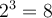 et
et ![\sqrt[3]{-8} = -2 \sqrt[3]{-8} = -2](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e35127b50d2299061c129f4a280158b4.png) , car
, car 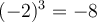 . Ainsi, -2 est la racine cubique de -8 et 2 est la racine cubique de 8. Remarquons que la racine n-ième impaire d'un nombre négatif est un nombre négatif, et que la racine n-ième d'un nombre positif est un nombre positif. Ils sont donc toujours du même signe.
. Ainsi, -2 est la racine cubique de -8 et 2 est la racine cubique de 8. Remarquons que la racine n-ième impaire d'un nombre négatif est un nombre négatif, et que la racine n-ième d'un nombre positif est un nombre positif. Ils sont donc toujours du même signe.
Exposants fractionnaires
Certaines propriétés s'appliquent aux exposants fractionnaires. Elles servent à simplifier plusieurs expressions contenant des radicaux.
* Note : Si  est pair, il faut s'assurer que
est pair, il faut s'assurer que  et
et 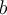 sont tous deux positifs avant de décomposer le produit ou le quotient. Par exemple, on peut écrire
sont tous deux positifs avant de décomposer le produit ou le quotient. Par exemple, on peut écrire 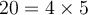 ou
ou 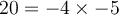 . Mais
. Mais 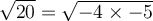 ne peut pas être décomposée en
ne peut pas être décomposée en 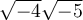 , car la racine carrée d'un nombre négatif n'existe pas. On ne pourrait pas appliquer la propriété 3 dans ce cas.
, car la racine carrée d'un nombre négatif n'existe pas. On ne pourrait pas appliquer la propriété 3 dans ce cas.
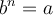
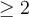
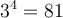
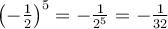
![\sqrt[n]{a} =b \sqrt[n]{a} =b](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ccda0126aa1dd4d989d2797a5523720c.png)
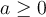
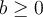
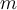
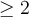
![\begin{array}{lll}1.&\sqrt[n]{a}=a^{1/n} &\text{ex. }\sqrt[5]{32}=32^{1/5}\\2.&\sqrt[n]{a^m}=a^{m/n}=\left(\sqrt[n]{a}\right)^m &\text{ex. } 8^{2/3}=\left(\sqrt[3]{8}\right)^2=(2)^2=4\\3.&\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}\text{ (voir note *)}&\text{ex. }\sqrt[3]{40}=\sqrt[3]{8\cdot 5}=\sqrt[3]{8}\sqrt[3]{5}=2\sqrt[3]{5}\\4.&\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ (voir note *)}&\text{ex. }\dfrac{\sqrt{20}}{\sqrt{5}}=\sqrt{\dfrac{20}{5}}=\sqrt{4}=2\\5.&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}&\text{ex. } \sqrt[3]{\sqrt{125}}=\sqrt[6]{125}\\6.&\sqrt[n]{a^n}=a\text{ si n est impair}&\text{ex. } \sqrt[3]{(-2)^3}=-2\\7.&\sqrt[n]{a^n}=|a|\text{ si n est pair}&\text{ex. } \sqrt{(-6)^2}=\sqrt{36}=|-6|=6\end{array} \begin{array}{lll}1.&\sqrt[n]{a}=a^{1/n} &\text{ex. }\sqrt[5]{32}=32^{1/5}\\2.&\sqrt[n]{a^m}=a^{m/n}=\left(\sqrt[n]{a}\right)^m &\text{ex. } 8^{2/3}=\left(\sqrt[3]{8}\right)^2=(2)^2=4\\3.&\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}\text{ (voir note *)}&\text{ex. }\sqrt[3]{40}=\sqrt[3]{8\cdot 5}=\sqrt[3]{8}\sqrt[3]{5}=2\sqrt[3]{5}\\4.&\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ (voir note *)}&\text{ex. }\dfrac{\sqrt{20}}{\sqrt{5}}=\sqrt{\dfrac{20}{5}}=\sqrt{4}=2\\5.&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}&\text{ex. } \sqrt[3]{\sqrt{125}}=\sqrt[6]{125}\\6.&\sqrt[n]{a^n}=a\text{ si n est impair}&\text{ex. } \sqrt[3]{(-2)^3}=-2\\7.&\sqrt[n]{a^n}=|a|\text{ si n est pair}&\text{ex. } \sqrt{(-6)^2}=\sqrt{36}=|-6|=6\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/b7df3c7f2c784e3fc46fd293f240e725.png)
![\dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}} \dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9abd596b4018e90f3dd146be6133ed07.png)
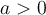
![\begin{array}{ll} \dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}} & = \dfrac{\sqrt[3]{2^6}\sqrt[3]{a^3}}{\sqrt{2^3}\sqrt{a}} \\[1em] & = \dfrac{(2^6)^{\frac{1}{3}} a}{(2^3)^{\frac{1}{2}} a^{\frac{1}{2}}} \\[1em]{} & =\dfrac{2^2 a}{2^{\frac{3}{2}} a^{\frac{1}{2}}}\\[1em]{} & = 2^{2-\frac{3}{2}} a^{1-\frac{1}{2}} \\[1em]{} & = 2^{\frac{1}{2}} a^{\frac{1}{2}} \\& = (2a)^{\frac{1}{2}}=\sqrt{2a}\end{array} \begin{array}{ll} \dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}} & = \dfrac{\sqrt[3]{2^6}\sqrt[3]{a^3}}{\sqrt{2^3}\sqrt{a}} \\[1em] & = \dfrac{(2^6)^{\frac{1}{3}} a}{(2^3)^{\frac{1}{2}} a^{\frac{1}{2}}} \\[1em]{} & =\dfrac{2^2 a}{2^{\frac{3}{2}} a^{\frac{1}{2}}}\\[1em]{} & = 2^{2-\frac{3}{2}} a^{1-\frac{1}{2}} \\[1em]{} & = 2^{\frac{1}{2}} a^{\frac{1}{2}} \\& = (2a)^{\frac{1}{2}}=\sqrt{2a}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/10075424277b9f5957f4ad39054829e5.png)
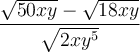

![\begin{array}{ll}\dfrac{ \sqrt{50xy}-\sqrt{18xy}}{\sqrt{2xy^5}}&=\dfrac{\sqrt{25\cdot 2\cdot xy}-\sqrt{9\cdot 2\cdot xy}}{\sqrt{2x\cdot y\cdot y^4}}\\[1em]&=\dfrac{\sqrt{25}\sqrt{2xy}-\sqrt{9}\sqrt{2xy}}{\sqrt{2xy}\sqrt{y^4}}\\[1em]&=\dfrac{5\sqrt{2xy}-3\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2}{y^2}\text{ si }x\neq 0\text{ et }y\neq 0\end{array} \begin{array}{ll}\dfrac{ \sqrt{50xy}-\sqrt{18xy}}{\sqrt{2xy^5}}&=\dfrac{\sqrt{25\cdot 2\cdot xy}-\sqrt{9\cdot 2\cdot xy}}{\sqrt{2x\cdot y\cdot y^4}}\\[1em]&=\dfrac{\sqrt{25}\sqrt{2xy}-\sqrt{9}\sqrt{2xy}}{\sqrt{2xy}\sqrt{y^4}}\\[1em]&=\dfrac{5\sqrt{2xy}-3\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2}{y^2}\text{ si }x\neq 0\text{ et }y\neq 0\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/a8f5b7fa526e62ecf20db36c7099fb37.png)
![\dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}} \dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8528515def1a970619795b94647f252d.png)
![\begin{array}{ll}\dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}}&= \dfrac{a^{\frac{1}{3}}a^{\frac{5}{2}}}{(81a)^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{1}{3}+\frac{5}{2}}}{81^{\frac{3}{4}}a^{\frac{3}{4}}}=\dfrac{a^{\frac{17}{6}}}{(3^4)^{\frac{3}{4}}a^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{17}{6}-\frac{3}{4}}}{3^3}=\dfrac{a^{\frac{25}{12}}}{27}\end{array} \begin{array}{ll}\dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}}&= \dfrac{a^{\frac{1}{3}}a^{\frac{5}{2}}}{(81a)^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{1}{3}+\frac{5}{2}}}{81^{\frac{3}{4}}a^{\frac{3}{4}}}=\dfrac{a^{\frac{17}{6}}}{(3^4)^{\frac{3}{4}}a^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{17}{6}-\frac{3}{4}}}{3^3}=\dfrac{a^{\frac{25}{12}}}{27}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e0b020037ec4228f05f52826e3085aae.png)
 Racines et exposants fractionnaires
Racines et exposants fractionnaires