1.1 Les polynômes et les racines
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 1.1 Les polynômes et les racines |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 08:39 |
Description
- Définitions
- Opérations sur les polynômes
- Racines et exposants fractionnaires
1. Définitions
 Un monôme est une expression algébrique formée du produit entre une constante réelle
Un monôme est une expression algébrique formée du produit entre une constante réelle 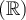 et une ou plusieurs variables. Chacune de ces variables est affectée d’un exposant entier positif ou nul
et une ou plusieurs variables. Chacune de ces variables est affectée d’un exposant entier positif ou nul 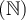 .
.
 Un polynôme est une expression algébrique formée d’une somme de monômes. Chaque monôme est un terme du polynôme.
Un polynôme est une expression algébrique formée d’une somme de monômes. Chaque monôme est un terme du polynôme.
2. Opérations sur les polynômes
Pour additionner deux polynômes, il suffit d’additionner les coefficients de leurs termes semblables, c’est-à-dire des termes qui ont les mêmes variables affectées des mêmes exposants.
Pour soustraire deux polynômes, 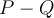 , il suffit de soustraire les coefficients de leurs termes semblables.
, il suffit de soustraire les coefficients de leurs termes semblables.
Pour multiplier des expressions algébriques, on doit utiliser les propriétés des exposants. Par exemple, si l’on multiplie deux monômes, il faut d’abord multiplier les coefficients, puis multiplier les variables semblables entre elles en additionnant leurs exposants.
Si l'on veut multiplier deux polynômes, il faut multiplier chaque terme du premier polynôme par chaque terme du second. On utilise donc la propriété de distributivité de la multiplication sur l’addition.
La division de deux monômes, tout comme la multiplication, fait appel aux propriétés des exposants. De façon similaire, on divise d'abord les coefficients, puis on divise les variables semblables en soustrayant leurs exposants.
Pour diviser un polynôme par un monôme, on n'a qu'à diviser chaque terme du polynôme par ce monôme.
Pour diviser deux polynômes entre eux, on procède comme pour la division de deux entiers. On cherche leur quotient et parfois, on obtient un reste.
|
On écrit les termes de chaque polynôme dans l’ordre décroissant des degrés. |
|
|
On divise le premier terme du dividende par le premier terme du diviseur. |
|
|
On multiplie chaque terme du diviseur par le premier terme du quotient. |
|
|
On soustrait les deux polynômes. |
|
|
On continue de la même façon jusqu'à ce que le degré du reste (ici le degré est 0) soit inférieur au degré du diviseur (ici le degré est 1). La division est alors terminée. |
|
|
La réponse est le quotient, additionné de la fraction formée par le reste sur le diviseur. |
Exercices formatifs WeBWorK
 Opérations sur les polynômes
Opérations sur les polynômes
3. Racines et exposants fractionnaires
Par exemple :
Racines paires
Pour calculer la racine n-ième paire d'un nombre  , il faut respecter ces deux règles :
, il faut respecter ces deux règles :
- Le nombre
 ne doit pas être négatif, c'est-à-dire que
ne doit pas être négatif, c'est-à-dire que 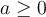 .
. - Le nombre
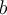 , qui est la racine n-ième de
, qui est la racine n-ième de  , ne doit pas être négatif non plus.
, ne doit pas être négatif non plus.
En effet, si  , alors
, alors ![\sqrt[n]{a} \sqrt[n]{a}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.png) n'existe pas pour les entiers
n'existe pas pour les entiers  pairs. Par exemple,
pairs. Par exemple,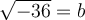 n'existe pas, car il n'existe aucun nombre réel
n'existe pas, car il n'existe aucun nombre réel 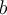 tel que
tel que 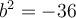 .
.
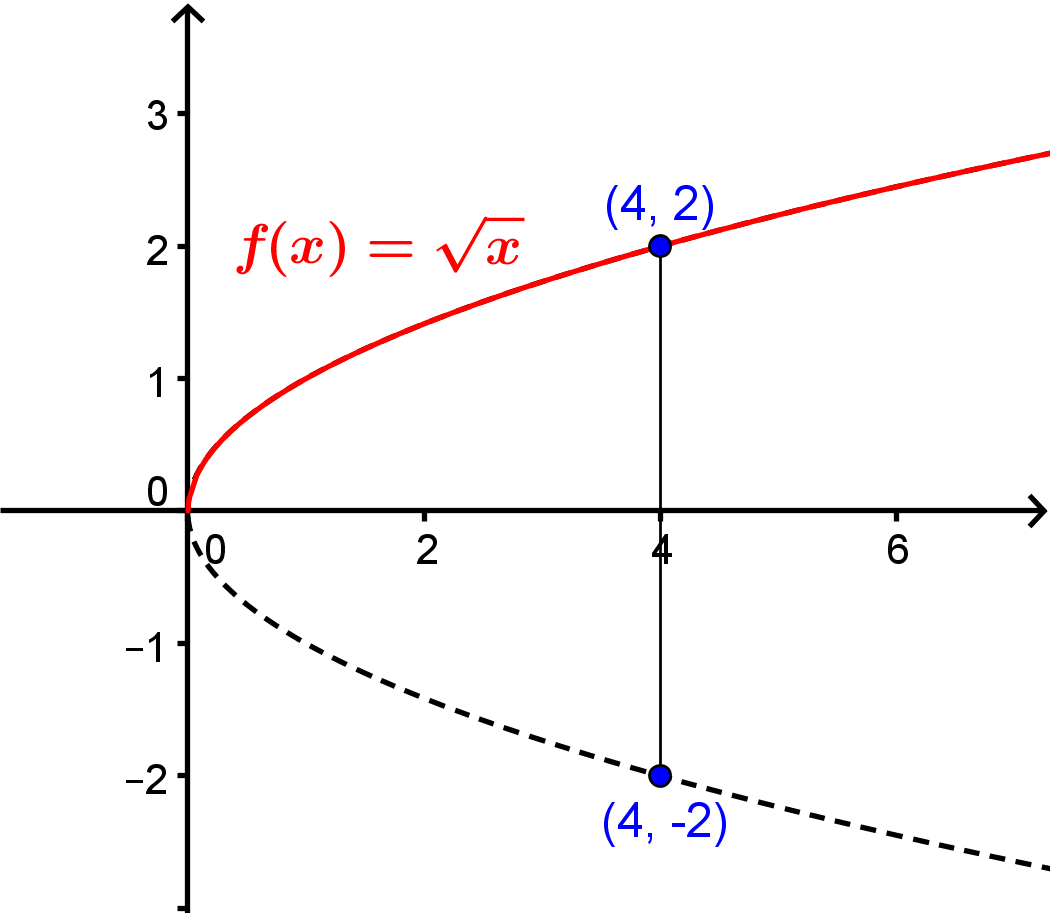
De plus, même si 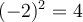 et que
et que 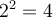 , on dira que
, on dira que 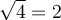 , soit la racine positive de 4. Il ne faut jamais écrire
, soit la racine positive de 4. Il ne faut jamais écrire 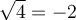 , car la racine carrée doit être une fonction par définition, c'est-à-dire qu'à toute valeur de
, car la racine carrée doit être une fonction par définition, c'est-à-dire qu'à toute valeur de  doit correspondre une seule image
doit correspondre une seule image 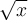 . Cette notion est expliquée plus en détails dans la section sur les fonctions, mais la figure ci-contre illustre bien ce cas.
. Cette notion est expliquée plus en détails dans la section sur les fonctions, mais la figure ci-contre illustre bien ce cas.
Racines impaires
Contrairement à la racine paire, la racine n-ième impaire d'un nombre  est toujours définie. Dans ce cas, on a
est toujours définie. Dans ce cas, on a
Par exemple, on aura ![\sqrt[3]{8} = 2 \sqrt[3]{8} = 2](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/aae2ac845a729da53b6a3a79cc4458ae.png) , car
, car 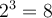 et
et ![\sqrt[3]{-8} = -2 \sqrt[3]{-8} = -2](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e35127b50d2299061c129f4a280158b4.png) , car
, car 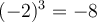 . Ainsi, -2 est la racine cubique de -8 et 2 est la racine cubique de 8. Remarquons que la racine n-ième impaire d'un nombre négatif est un nombre négatif, et que la racine n-ième d'un nombre positif est un nombre positif. Ils sont donc toujours du même signe.
. Ainsi, -2 est la racine cubique de -8 et 2 est la racine cubique de 8. Remarquons que la racine n-ième impaire d'un nombre négatif est un nombre négatif, et que la racine n-ième d'un nombre positif est un nombre positif. Ils sont donc toujours du même signe.
Exposants fractionnaires
Certaines propriétés s'appliquent aux exposants fractionnaires. Elles servent à simplifier plusieurs expressions contenant des radicaux.
* Note : Si  est pair, il faut s'assurer que
est pair, il faut s'assurer que  et
et 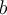 sont tous deux positifs avant de décomposer le produit ou le quotient. Par exemple, on peut écrire
sont tous deux positifs avant de décomposer le produit ou le quotient. Par exemple, on peut écrire 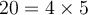 ou
ou 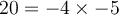 . Mais
. Mais 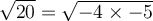 ne peut pas être décomposée en
ne peut pas être décomposée en 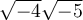 , car la racine carrée d'un nombre négatif n'existe pas. On ne pourrait pas appliquer la propriété 3 dans ce cas.
, car la racine carrée d'un nombre négatif n'existe pas. On ne pourrait pas appliquer la propriété 3 dans ce cas.
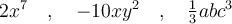
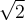
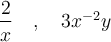
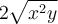
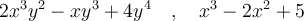
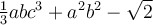
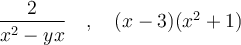
![\quad\sqrt[3]{a + 2ab^2}\quad \quad\sqrt[3]{a + 2ab^2}\quad](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6ec47910d2a3c054df26cbb81c12a4f5.png)

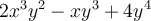
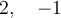
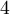
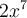
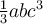
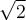
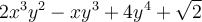
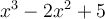
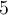
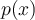
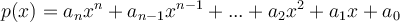
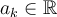
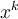
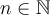
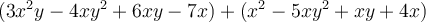
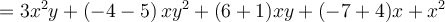
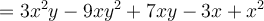
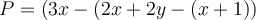
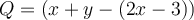
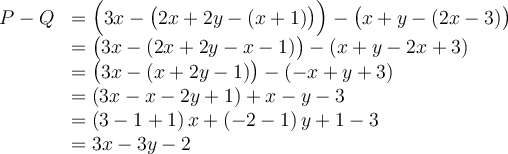
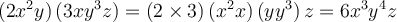
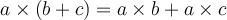
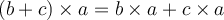
![\begin{array}{ll} & \left({x^2-xy+y^2}\right)\left({x+2y}\right) \\[0.8em] = & x^2\left({x+2y}\right)-xy\left({x+2y}\right)+y^2\left({x+2y}\right) \\[0.8em] = & x^3+2x^2y-x^2y-2xy^2+xy^2+2y^3 \\[0.8em] = & x^3+x^2y-2xy^2+xy^2+2y^3 \end{array} \begin{array}{ll} & \left({x^2-xy+y^2}\right)\left({x+2y}\right) \\[0.8em] = & x^2\left({x+2y}\right)-xy\left({x+2y}\right)+y^2\left({x+2y}\right) \\[0.8em] = & x^3+2x^2y-x^2y-2xy^2+xy^2+2y^3 \\[0.8em] = & x^3+x^2y-2xy^2+xy^2+2y^3 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9d4145254d6cc9353ddd647acbea706f.png)
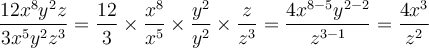
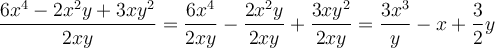
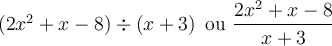
![\begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{}&{ \; 2x}\end{array} \begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{}&{ \; 2x}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/45e1884188796305f287aad16c13af37.png)
![\begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em] {2{x^2} + 6x}&{ \; 2x}\end{array} \begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em] {2{x^2} + 6x}&{ \; 2x}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ed38630d199ae75d7a2a5725833f81a1.png)
![\begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2}+6x} \right) \quad} }&{ \; 2x}\\[0.5em]{\quad \quad \quad -5x-8}&{}\end{array} \begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2}+6x} \right) \quad} }&{ \; 2x}\\[0.5em]{\quad \quad \quad -5x-8}&{}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/89fd50daa1a497b590b2dc40c0c78464.png)
![\begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x + 3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2} + 6x} \right) \quad} }&{ \; 2x-5}\\[0.5em]{\quad \quad \quad -5x-8}&{}\\[0.5em]{\underline {\quad \quad -\left( {-5x-15} \right)}}&{}\\[0.5em]{\qquad \qquad \qquad 7}&{}\end{array} \begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x + 3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2} + 6x} \right) \quad} }&{ \; 2x-5}\\[0.5em]{\quad \quad \quad -5x-8}&{}\\[0.5em]{\underline {\quad \quad -\left( {-5x-15} \right)}}&{}\\[0.5em]{\qquad \qquad \qquad 7}&{}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2e36e3b4330caab098785a0987cda9c8.png)
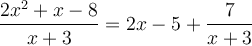
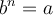
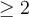
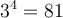
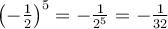
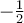
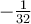
![\sqrt[n]{a} =b \sqrt[n]{a} =b](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ccda0126aa1dd4d989d2797a5523720c.png)
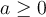
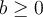
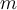
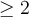
![\begin{array}{lll}1.&\sqrt[n]{a}=a^{1/n} &\text{ex. }\sqrt[5]{32}=32^{1/5}\\2.&\sqrt[n]{a^m}=a^{m/n}=\left(\sqrt[n]{a}\right)^m &\text{ex. } 8^{2/3}=\left(\sqrt[3]{8}\right)^2=(2)^2=4\\3.&\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}\text{ (voir note *)}&\text{ex. }\sqrt[3]{40}=\sqrt[3]{8\cdot 5}=\sqrt[3]{8}\sqrt[3]{5}=2\sqrt[3]{5}\\4.&\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ (voir note *)}&\text{ex. }\dfrac{\sqrt{20}}{\sqrt{5}}=\sqrt{\dfrac{20}{5}}=\sqrt{4}=2\\5.&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}&\text{ex. } \sqrt[3]{\sqrt{125}}=\sqrt[6]{125}\\6.&\sqrt[n]{a^n}=a\text{ si n est impair}&\text{ex. } \sqrt[3]{(-2)^3}=-2\\7.&\sqrt[n]{a^n}=|a|\text{ si n est pair}&\text{ex. } \sqrt{(-6)^2}=\sqrt{36}=|-6|=6\end{array} \begin{array}{lll}1.&\sqrt[n]{a}=a^{1/n} &\text{ex. }\sqrt[5]{32}=32^{1/5}\\2.&\sqrt[n]{a^m}=a^{m/n}=\left(\sqrt[n]{a}\right)^m &\text{ex. } 8^{2/3}=\left(\sqrt[3]{8}\right)^2=(2)^2=4\\3.&\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}\text{ (voir note *)}&\text{ex. }\sqrt[3]{40}=\sqrt[3]{8\cdot 5}=\sqrt[3]{8}\sqrt[3]{5}=2\sqrt[3]{5}\\4.&\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}\text{ (voir note *)}&\text{ex. }\dfrac{\sqrt{20}}{\sqrt{5}}=\sqrt{\dfrac{20}{5}}=\sqrt{4}=2\\5.&\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}&\text{ex. } \sqrt[3]{\sqrt{125}}=\sqrt[6]{125}\\6.&\sqrt[n]{a^n}=a\text{ si n est impair}&\text{ex. } \sqrt[3]{(-2)^3}=-2\\7.&\sqrt[n]{a^n}=|a|\text{ si n est pair}&\text{ex. } \sqrt{(-6)^2}=\sqrt{36}=|-6|=6\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/b7df3c7f2c784e3fc46fd293f240e725.png)
![\dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}} \dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9abd596b4018e90f3dd146be6133ed07.png)
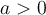
![\begin{array}{ll} \dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}} & = \dfrac{\sqrt[3]{2^6}\sqrt[3]{a^3}}{\sqrt{2^3}\sqrt{a}} \\[1em] & = \dfrac{(2^6)^{\frac{1}{3}} a}{(2^3)^{\frac{1}{2}} a^{\frac{1}{2}}} \\[1em]{} & =\dfrac{2^2 a}{2^{\frac{3}{2}} a^{\frac{1}{2}}}\\[1em]{} & = 2^{2-\frac{3}{2}} a^{1-\frac{1}{2}} \\[1em]{} & = 2^{\frac{1}{2}} a^{\frac{1}{2}} \\& = (2a)^{\frac{1}{2}}=\sqrt{2a}\end{array} \begin{array}{ll} \dfrac{\sqrt[3]{64a^3}}{\sqrt{8a}} & = \dfrac{\sqrt[3]{2^6}\sqrt[3]{a^3}}{\sqrt{2^3}\sqrt{a}} \\[1em] & = \dfrac{(2^6)^{\frac{1}{3}} a}{(2^3)^{\frac{1}{2}} a^{\frac{1}{2}}} \\[1em]{} & =\dfrac{2^2 a}{2^{\frac{3}{2}} a^{\frac{1}{2}}}\\[1em]{} & = 2^{2-\frac{3}{2}} a^{1-\frac{1}{2}} \\[1em]{} & = 2^{\frac{1}{2}} a^{\frac{1}{2}} \\& = (2a)^{\frac{1}{2}}=\sqrt{2a}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/10075424277b9f5957f4ad39054829e5.png)
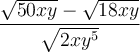

![\begin{array}{ll}\dfrac{ \sqrt{50xy}-\sqrt{18xy}}{\sqrt{2xy^5}}&=\dfrac{\sqrt{25\cdot 2\cdot xy}-\sqrt{9\cdot 2\cdot xy}}{\sqrt{2x\cdot y\cdot y^4}}\\[1em]&=\dfrac{\sqrt{25}\sqrt{2xy}-\sqrt{9}\sqrt{2xy}}{\sqrt{2xy}\sqrt{y^4}}\\[1em]&=\dfrac{5\sqrt{2xy}-3\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2}{y^2}\text{ si }x\neq 0\text{ et }y\neq 0\end{array} \begin{array}{ll}\dfrac{ \sqrt{50xy}-\sqrt{18xy}}{\sqrt{2xy^5}}&=\dfrac{\sqrt{25\cdot 2\cdot xy}-\sqrt{9\cdot 2\cdot xy}}{\sqrt{2x\cdot y\cdot y^4}}\\[1em]&=\dfrac{\sqrt{25}\sqrt{2xy}-\sqrt{9}\sqrt{2xy}}{\sqrt{2xy}\sqrt{y^4}}\\[1em]&=\dfrac{5\sqrt{2xy}-3\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2\sqrt{2xy}}{y^2\sqrt{2xy}}\\[1em]&=\dfrac{2}{y^2}\text{ si }x\neq 0\text{ et }y\neq 0\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/a8f5b7fa526e62ecf20db36c7099fb37.png)
![\dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}} \dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8528515def1a970619795b94647f252d.png)
![\begin{array}{ll}\dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}}&= \dfrac{a^{\frac{1}{3}}a^{\frac{5}{2}}}{(81a)^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{1}{3}+\frac{5}{2}}}{81^{\frac{3}{4}}a^{\frac{3}{4}}}=\dfrac{a^{\frac{17}{6}}}{(3^4)^{\frac{3}{4}}a^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{17}{6}-\frac{3}{4}}}{3^3}=\dfrac{a^{\frac{25}{12}}}{27}\end{array} \begin{array}{ll}\dfrac{\sqrt[3]{a}\sqrt{a^5}}{\sqrt[4]{(81a)^3}}&= \dfrac{a^{\frac{1}{3}}a^{\frac{5}{2}}}{(81a)^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{1}{3}+\frac{5}{2}}}{81^{\frac{3}{4}}a^{\frac{3}{4}}}=\dfrac{a^{\frac{17}{6}}}{(3^4)^{\frac{3}{4}}a^{\frac{3}{4}}}\\[1em]&=\dfrac{a^{\frac{17}{6}-\frac{3}{4}}}{3^3}=\dfrac{a^{\frac{25}{12}}}{27}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e0b020037ec4228f05f52826e3085aae.png)
 Racines et exposants fractionnaires
Racines et exposants fractionnaires