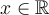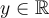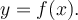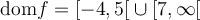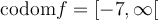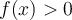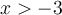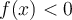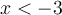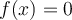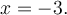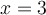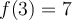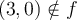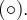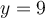2.1 Les fonctions
- Relation et fonction
- Domaine et image
- Graphique d'une fonction
- Points d'intersection avec les axes
3. Graphique d'une fonction
Chaque couple 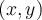 appartenant à une fonction réelle
appartenant à une fonction réelle  peut être représenté par un point dans le plan cartésien.
peut être représenté par un point dans le plan cartésien.  est alors l'abcisse et
est alors l'abcisse et  l'ordonnée du point dans le plan. On peut ainsi donner une représentation graphique d'une fonction qui dépend notamment de son domaine et de son équation.
l'ordonnée du point dans le plan. On peut ainsi donner une représentation graphique d'une fonction qui dépend notamment de son domaine et de son équation.
Exemple :
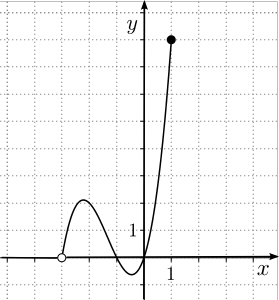
Le graphique ci-contre représente la fonction 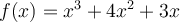 , où le
, où le ![\text{dom}f = \left]{-3,1}\right]. \text{dom}f = \left]{-3,1}\right].](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/a49914b0c0a9f5bcb62d3e9d39f3bf18.png)
Puisque le domaine est l'intervalle réel ![\left]{-3,1}\right], \left]{-3,1}\right],](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6360ae1fb0eba421f34bf4d5c1455cc6.png) le graphique est constitué d'une infinité de points. À partir d'un tableau de valeurs, il est possible d'obtenir quelques points du graphique en remplaçant les valeurs de
le graphique est constitué d'une infinité de points. À partir d'un tableau de valeurs, il est possible d'obtenir quelques points du graphique en remplaçant les valeurs de  dans l'équation.
dans l'équation.
 |
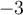 |
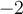 |
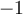 |
 |
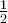 |
 |
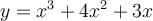 |
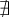 |
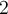 |
 |
 |
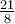 |
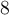 |
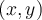 |
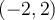 |
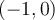 |
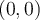 |
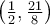 |
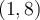 |
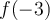 n'est pas défini, puisque
n'est pas défini, puisque 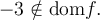 On indique donc un point vide
On indique donc un point vide 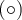 à l'extrémité gauche du graphique.
à l'extrémité gauche du graphique.
Puisque 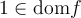 , on peut calculer
, on peut calculer 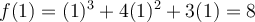 et on place un point plein
et on place un point plein  à l'autre extrémité pour indiquer que le point
à l'autre extrémité pour indiquer que le point 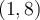 appartient à la courbe.
appartient à la courbe.
Un tableau de valeurs est utile pour tracer une esquisse, mais il ne permet pas de connaître avec certitude la forme de la courbe entre ces points. Nous verrons plus loin quelques modèles de fonctions courantes et les caractéristiques de leur graphique.
Test de la droite verticale
Le test de la droite verticale nous permet de déterminer si un graphique représente une fonction et non seulement une relation.
Par exemple :
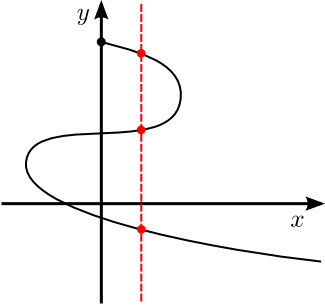
Le graphique ci-contre n'est pas celui d'une fonction, car il existe entre autres une droite verticale qui coupe la courbe en trois points, soit plus d'un point.
Le graphique d'une fonction peut révéler plusieurs informations. On peut par exemple visualiser :
- Le domaine et le codomaine;
- Les points qui croisent les axes de coordonnées;
- Le signe de la fonction;
- Les extremums de la fonction.
Exemple :
-
 Cochez la case dom f, puis faites bouger le curseur « Valeur de x ». Le tracé en rouge correspond aux valeurs de
Cochez la case dom f, puis faites bouger le curseur « Valeur de x ». Le tracé en rouge correspond aux valeurs de  possédant une image
possédant une image 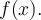
-
 Cochez la case codom f, puis faites bouger le curseur « Valeur de x ». Le tracé en vert correspond aux valeurs de
Cochez la case codom f, puis faites bouger le curseur « Valeur de x ». Le tracé en vert correspond aux valeurs de 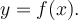
-
 En cochant la case Signe de la fonction et en modifiant toujours la valeur de
En cochant la case Signe de la fonction et en modifiant toujours la valeur de  , vous pouvez voir lorsque la fonction est positive et lorsqu'elle est négative. En effet, pour tout
, vous pouvez voir lorsque la fonction est positive et lorsqu'elle est négative. En effet, pour tout 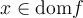 :
: