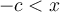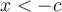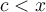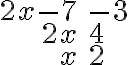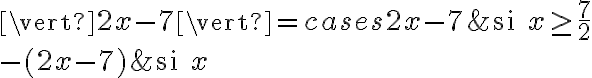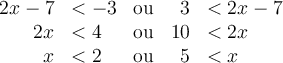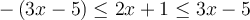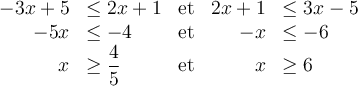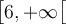1.5 Les inéquations
- Principes pour résoudre une inéquation
- Résoudre une inéquation à l'aide d'un tableau de signes
- Résoudre une inéquation contenant des valeurs absolues
3. Résoudre une inéquation contenant des valeurs absolues
Nous pouvons séparer en deux cas les inéquations contenant une valeur absolue pour bien comprendre comment les résoudre.
- Si
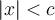 (ou
(ou 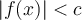 )
)
Les valeurs de
 qui vérifient cette inéquation appartiennent à l'intervalle
qui vérifient cette inéquation appartiennent à l'intervalle ![\left[{-c, c}\right] \left[{-c, c}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f7052b8b0777d8a957d26db66dda4e0c.png) . Il faut donc que
. Il faut donc que 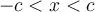 , c'est-à-dire que
, c'est-à-dire que  soit à la fois supérieur à
soit à la fois supérieur à 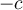 et inférieur à
et inférieur à 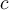 .
.Notre démarche consiste donc à chercher des solutions communes aux deux inéquations :
- Si
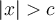 (ou
(ou 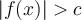 )
)
Les valeurs de
 qui vérifient cette inéquation appartiennent aux intervalles
qui vérifient cette inéquation appartiennent aux intervalles ![\left]{-\infty,-c}\right] \left]{-\infty,-c}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9092c823218dd70d62c18280c65a5ac1.png) ou
ou 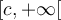 , c'est-à-dire que
, c'est-à-dire que  peut être inférieur à
peut être inférieur à 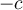 ou bien supérieur à
ou bien supérieur à 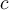 .
.Notre démarche consiste donc à faire l'union des ensembles solutions de ces deux inéquations :
Exemples :
a) Trouvons l'ensemble solution de l'inéquation 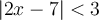 .
.
Il faut trouver les valeurs de  telles que l'expression à l'intérieur de la valeur absolue est à la fois inférieure à
telles que l'expression à l'intérieur de la valeur absolue est à la fois inférieure à 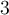 et supérieure à
et supérieure à 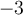 , c'est-à-dire
, c'est-à-dire 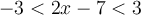 .
.
Il faut résoudre les deux inéquations suivantes et à faire l'intersection des deux ensembles solutions.
Aidons nous du graphique Geogebra ci-dessous pour comprendre la solution de cette inéquation. ![]() En déplaçant le point vert sur la droite, on peut voir le résultat de la valeur absolue
En déplaçant le point vert sur la droite, on peut voir le résultat de la valeur absolue 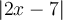 pour certaines valeurs de
pour certaines valeurs de  . L'ensemble solution contient toutes les valeurs de
. L'ensemble solution contient toutes les valeurs de  qui sont à la fois inférieures à
qui sont à la fois inférieures à 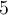 et supérieures à
et supérieures à 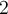 , c'est-à-dire les valeurs de
, c'est-à-dire les valeurs de  qui appartiennent à l'intervalle
qui appartiennent à l'intervalle ![\left]2,5\right[, \left]2,5\right[,](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/bcc62aaa4e24d29008d1ad343249bfb8.png) comme le montre la trace en bleue sur l'axe des
comme le montre la trace en bleue sur l'axe des  .
.
De plus, on remarque que pour 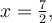 l'intérieur de la valeur absolue est nul, car
l'intérieur de la valeur absolue est nul, car 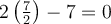 . Ainsi, lorsque
. Ainsi, lorsque  l'intérieur de la valeur absolue devient négatif, soit
l'intérieur de la valeur absolue devient négatif, soit 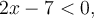 et lorsque
et lorsque 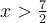 , l'intérieur devient positif, soit
, l'intérieur devient positif, soit 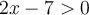 . Cela correspond bien à la définition de la valeur absolue :
. Cela correspond bien à la définition de la valeur absolue :
b) Trouvons l'ensemble solution de l'inéquation 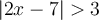 .
.
Il faut trouver les valeurs de  qui appartiennent à l'un ou l'autre des ensembles solutions des deux inéquations :
qui appartiennent à l'un ou l'autre des ensembles solutions des deux inéquations :
Il faut faire l'union de ces deux ensembles que l'on a représentés sur l'axe réel suivant :

Les valeurs de  peuvent donc appartenir à l'intervalle
peuvent donc appartenir à l'intervalle ![\left]-\infty, 2\right[ \left]-\infty, 2\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/985af0e347708f0b302c0374c1e44f50.png) ou bien à l'intervalle
ou bien à l'intervalle ![\left]{5, +\infty}\right[ \left]{5, +\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f96c4f335e3d8de6db3ca39e7b6bbcbd.png) .
.
L'ensemble solution de l'inéquation 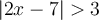 est donc
est donc ![\Bigl]{-\infty, 2}\Bigr[ \cup \Bigl]{5, +\infty}\Bigr[ \Bigl]{-\infty, 2}\Bigr[ \cup \Bigl]{5, +\infty}\Bigr[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f7b08192686b439561617325958f062c.png) .
.
c) Trouvons l'ensemble solution de l'inéquation 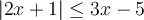 .
.
Il faut trouver les valeurs de  qui sont communes aux ensembles solutions des deux inéquations :
qui sont communes aux ensembles solutions des deux inéquations :
Il faut faire l'intersection de ces deux ensembles que l'on a représentés sur l'axe réel suivant :

C'est-à-dire que les valeurs de  appartiennent à la fois à l'intervalle
appartiennent à la fois à l'intervalle 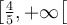 et à l'intervalle
et à l'intervalle 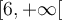 .
.