1.1 Les polynômes et les racines
- Définitions
- Opérations sur les polynômes
- Racines et exposants fractionnaires
2. Opérations sur les polynômes
Pour additionner deux polynômes, il suffit d’additionner les coefficients de leurs termes semblables, c’est-à-dire des termes qui ont les mêmes variables affectées des mêmes exposants.
Pour soustraire deux polynômes, 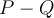 , il suffit de soustraire les coefficients de leurs termes semblables.
, il suffit de soustraire les coefficients de leurs termes semblables.
Pour multiplier des expressions algébriques, on doit utiliser les propriétés des exposants. Par exemple, si l’on multiplie deux monômes, il faut d’abord multiplier les coefficients, puis multiplier les variables semblables entre elles en additionnant leurs exposants.
Si l'on veut multiplier deux polynômes, il faut multiplier chaque terme du premier polynôme par chaque terme du second. On utilise donc la propriété de distributivité de la multiplication sur l’addition.
La division de deux monômes, tout comme la multiplication, fait appel aux propriétés des exposants. De façon similaire, on divise d'abord les coefficients, puis on divise les variables semblables en soustrayant leurs exposants.
Pour diviser un polynôme par un monôme, on n'a qu'à diviser chaque terme du polynôme par ce monôme.
Pour diviser deux polynômes entre eux, on procède comme pour la division de deux entiers. On cherche leur quotient et parfois, on obtient un reste.
|
On écrit les termes de chaque polynôme dans l’ordre décroissant des degrés. |
|
|
On divise le premier terme du dividende par le premier terme du diviseur. |
|
|
On multiplie chaque terme du diviseur par le premier terme du quotient. |
|
|
On soustrait les deux polynômes. |
|
|
On continue de la même façon jusqu'à ce que le degré du reste (ici le degré est 0) soit inférieur au degré du diviseur (ici le degré est 1). La division est alors terminée. |
|
|
La réponse est le quotient, additionné de la fraction formée par le reste sur le diviseur. |

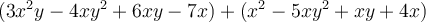
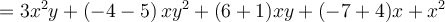
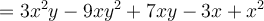
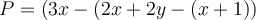
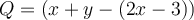
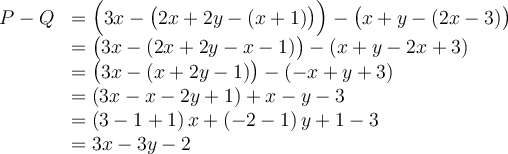
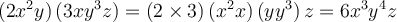
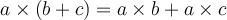
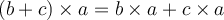
![\begin{array}{ll} & \left({x^2-xy+y^2}\right)\left({x+2y}\right) \\[0.8em] = & x^2\left({x+2y}\right)-xy\left({x+2y}\right)+y^2\left({x+2y}\right) \\[0.8em] = & x^3+2x^2y-x^2y-2xy^2+xy^2+2y^3 \\[0.8em] = & x^3+x^2y-2xy^2+xy^2+2y^3 \end{array} \begin{array}{ll} & \left({x^2-xy+y^2}\right)\left({x+2y}\right) \\[0.8em] = & x^2\left({x+2y}\right)-xy\left({x+2y}\right)+y^2\left({x+2y}\right) \\[0.8em] = & x^3+2x^2y-x^2y-2xy^2+xy^2+2y^3 \\[0.8em] = & x^3+x^2y-2xy^2+xy^2+2y^3 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9d4145254d6cc9353ddd647acbea706f.png)
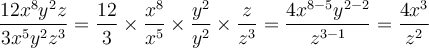
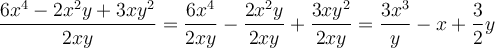
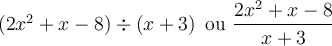
![\begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{}&{ \; 2x}\end{array} \begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{}&{ \; 2x}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/45e1884188796305f287aad16c13af37.png)
![\begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em] {2{x^2} + 6x}&{ \; 2x}\end{array} \begin{array}{ll}{2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em] {2{x^2} + 6x}&{ \; 2x}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ed38630d199ae75d7a2a5725833f81a1.png)
![\begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2}+6x} \right) \quad} }&{ \; 2x}\\[0.5em]{\quad \quad \quad -5x-8}&{}\end{array} \begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x+3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2}+6x} \right) \quad} }&{ \; 2x}\\[0.5em]{\quad \quad \quad -5x-8}&{}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/89fd50daa1a497b590b2dc40c0c78464.png)
![\begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x + 3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2} + 6x} \right) \quad} }&{ \; 2x-5}\\[0.5em]{\quad \quad \quad -5x-8}&{}\\[0.5em]{\underline {\quad \quad -\left( {-5x-15} \right)}}&{}\\[0.5em]{\qquad \qquad \qquad 7}&{}\end{array} \begin{array}{ll}{\quad 2{x^2} + x - 8}&{\left| {\underline {x + 3} } \right. }\\[0.5em]{\underline {- \left( {2{x^2} + 6x} \right) \quad} }&{ \; 2x-5}\\[0.5em]{\quad \quad \quad -5x-8}&{}\\[0.5em]{\underline {\quad \quad -\left( {-5x-15} \right)}}&{}\\[0.5em]{\qquad \qquad \qquad 7}&{}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2e36e3b4330caab098785a0987cda9c8.png)
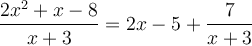
 Opérations sur les polynômes
Opérations sur les polynômes