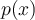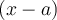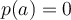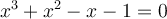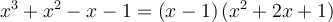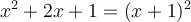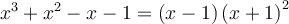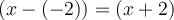1.2 La factorisation: Théorème de la factorisation

8. Théorème de la factorisation

Dans certain cas, nous pouvons également utiliser la division polynomiale pour nous aider à factoriser en déterminant auparavant un facteur 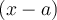$\left( {x - a} \right)$ .
Afin de trouver ce facteur, il faut appliquer le théorème de la factorisation :

Soit

$p(x)$ , un polynôme de degré

$n$ , alors

$(x-a)$ est un facteur de

$p(x)$

$\Leftrightarrow$

$x=a$ est un zéro de

$p(x)$ , donc si et seulement si

$p(a)=0$ .

Exemple 1 : Factorisons le polynôme 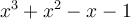$x^3 + x^2 - x -1$ sachant que 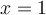$x=1$ est un zéro du polynôme.

Sachant que 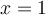$x = 1$ est un zéro de 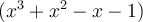$(x^3 + x^2 - x -1)$ , c'est-à-dire que

$x^3 + x^2 - x -1 = 0$ lorsque $x = 1$ ,

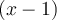alors $(x - 1)$ est un facteur linéaire de notre polynôme (de même, 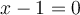$x - 1 = 0$ lorsque $x = 1$ ).

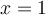Par conséquent, nous pouvons écrire :

$x^3 + x^2 - x -1 = (x - 1) q(x)$
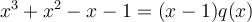
où 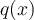$q(x)$ est un polynôme quadratrique de la forme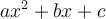 $ax^2+bx+c$

Nous trouvons le trinôme 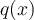$q(x)$ en effectuant la division polynomiale suivante.

$q(x) = \dfrac{x^3 +x^2-x-1}{x-1} \Rightarrow$

$\begin{array}{ll}{\phantom{-(\;}x^3+x^2-x-1}&{\left| {\underline {x - 1} } \right. }\\{\underline {- \left( {{x^3} -x^2} \right)} }&{x^2 + 2x + 1}\\\phantom{-(\;}{2x^2 -x-1}&{}\\{\underline {-\left( {2x^2 -2x} \right)}}&{}\\\phantom{-(\;}{x-1}&{}\\{\underline {-\left( {x-1} \right)}}&{} \\{\quad\quad 0}&{}\end{array}$

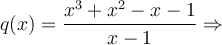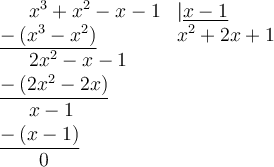Ainsi,

$x^3+x^2-x-1 = \left( {x-1} \right) \left( {x^2+2x+1} \right)$ .

Attention! La factorisation n'est pas terminée, car le facteur quadratique est réductible. On a que

$x^2+2x+1 = (x+1)^2$

La réponse finale est donc

$x^3+x^2-x-1 = \left( {x-1} \right) \left( {x+1} \right)^2$ .

Exemple 2 : Factorisons le binôme 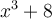${x^3} + 8$ .

Cherchons un zéro de 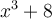${x^3} + 8$ , c'est-à-dire un nombre $x = a$ tel que ${x^3} + 8 = 0.$

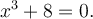
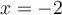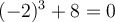Ce nombre est $x = - 2$ , car $(- 2)^3 + 8 = 0$ . Par conséquent, le facteur du polynôme 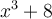$x^3+8$ est

$(x- (-2)) = (x + 2)$ .

Nous avons donc

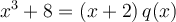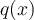$x^3 + 8 = \left( {x + 2} \right)q(x)$ où $q(x)$ est un polynôme de degré 2.

Nous trouvons le polynôme 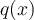$q(x)$ en effectuant une division polynomiale.

$q(x) = \dfrac{{x^3} + 8}{x+2} \Rightarrow$

$\begin{array}{rl}{{x^3} + 8}&{\left| {\underline {x + 2} } \right. }\\{\underline {- \left( {{x^3} + 2{x^2}} \right)} }&{ \; {x^2} - 2x + 4}\\{-2{x^2} + 8}&{}\\{\underline {-\left( {-2{x^2} - 4x} \right)}}&{}\\{4x+8}&{}\\{\underline {-\left( {4x + 8} \right)}}&{} \\{0}&{}\end{array}$

Ainsi, nous obtenons ${x^3} + 8 = \left( {x + 2} \right) \left( { {x^2} - 2x + 4 } \right)$

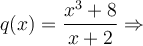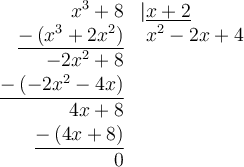Remarque : La factorisation est complète, car le facteur quadratique 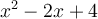$x^2-2x+4$ est irréductible puisque son discriminant 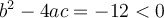$b^2-4ac = -12 < 0$ . Nous retrouvons le même résultat que celui obtenu en appliquant la formule de la somme de cubes.