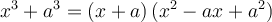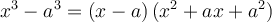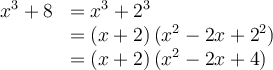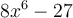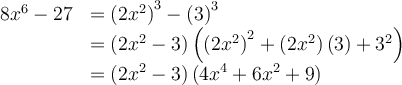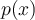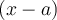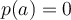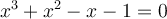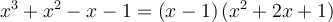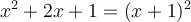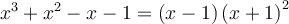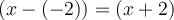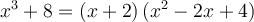1.2 La factorisation
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 1.2 La factorisation |
| Imprimé par: | Visiteur anonyme |
| Date: | dimanche 12 mai 2024, 02:43 |
Description
1. Introduction
Factoriser un polynôme signifie l'exprimer comme un produit de facteurs. Par exemple :
Ainsi, la factorisation d’un polynôme consiste à l’exprimer sous la forme d’un produit de polynômes de degré inférieur (facteurs).
N’oubliez pas que la factorisation d’un polynôme n’est pas toujours possible. Par exemple, 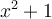 ne se factorise pas.
ne se factorise pas.
Ainsi, pour factoriser, il faut reconnaître le modèle du polynôme et utiliser l'une des méthodes appropriées décrites dans les pages suivantes.
2. Mise en évidence simple
La méthode de mise en évidence simple est utilisée lorsque tous les termes du polynôme contiennent un facteur commun. On se souvient que les termes dans une expression sont séparés par une addition ou une soustraction. Pour mettre en évidence ce facteur commun, on utilise la propriété de la distributivité de la multiplication sur l’addition :
Exemples : Factoriser les expressions suivantes.
Ce polynôme contient 3 termes et chacun des termes a 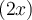 comme facteur commun:
comme facteur commun:
On remarque qu'en effectuant une distributivité sur la réponse, on revient à l'expression de départ :
Ce polynôme à deux variables contient également 3 termes et chacun a 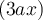 comme facteur commun :
comme facteur commun :
Cette expression contient seulement 2 termes, 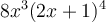 et
et 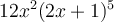 , qui sont séparés par une soustraction. Chacun des termes possèdent trois facteurs : une constante, une puissance de
, qui sont séparés par une soustraction. Chacun des termes possèdent trois facteurs : une constante, une puissance de  et une puissance de
et une puissance de 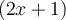 . Trouvons les facteurs communs :
. Trouvons les facteurs communs :
Les facteurs communs sont ceux en gras sous chacun des termes, alors en mettant en évidence ces facteurs on obtient :
3. Mise en évidence double
On utilise la double mise en évidence lorsque les termes, une fois regroupés par deux (ou par trois, par quatre, etc.) contiennent un facteur commun à chaque groupe de termes. Cette méthode est souvent utilisée lorsqu'il y a 4 termes ou 6 termes dans l'expression.
Après avoir regroupé les termes, on effectue deux mises en évidence simple successives, si possible.
4.1. Trinôme carré parfait
Lorsqu’on élève la somme de deux variables au carré, on constate qu'un des termes du polynôme correspond au double du produit de ces variables. En effet,
La factorisation trinôme carré parfait s’utilise seulement avec des polynômes qui s'écrivent comme une somme de trois termes ayant la forme suivante :
4.2. Trinôme général
On peut factoriser un trinôme général en suivant les étapes suivantes :
1. On cherche deux nombres 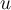 et
et 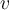 , dont la somme est
, dont la somme est 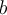 et le produit est
et le produit est 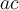 .
.
2. On remplace 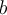 par la somme de ces deux nombres.
par la somme de ces deux nombres.
3. On effectue une mise en évidence double.
Exemples : Factorisons les trinômes suivants.
a)
On cherche deux nombres tels que
On effectue ensuite une double mise en évidence de la façon suivante :
4.3. Polynôme quadratique non factorisable
On dit qu'un polynôme quadratique de la forme 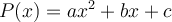 est irréductible s'il n'est pas factorisable, c'est-à-dire si on ne peut pas le décomposer en un produit de deux facteurs de degré 1. Voici la règle à respecter :
est irréductible s'il n'est pas factorisable, c'est-à-dire si on ne peut pas le décomposer en un produit de deux facteurs de degré 1. Voici la règle à respecter :
Par exemple, le polynôme 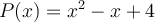 n'est pas factorisable, car
n'est pas factorisable, car 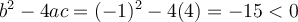 . De façon équivalente, on peut dire qu'il n'existe aucune valeur de
. De façon équivalente, on peut dire qu'il n'existe aucune valeur de  telle que
telle que 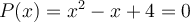 . Le graphique de cette fonction représente une courbe qui ne croisera jamais l'axe des
. Le graphique de cette fonction représente une courbe qui ne croisera jamais l'axe des  .
.
De même, une somme de deux carrés 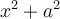 n’est pas décomposable en facteurs, car il n'existe aucune valeur réelle de
n’est pas décomposable en facteurs, car il n'existe aucune valeur réelle de  telle que
telle que 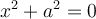 ou telle que
ou telle que 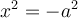 .
.
Le graphique Geogebra ci-dessous représente la fonction quadratique 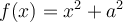 . Suivez les instructions et remarquez que la courbe de cette fonction ne croisera jamais l’axe des
. Suivez les instructions et remarquez que la courbe de cette fonction ne croisera jamais l’axe des  peu importe la valeur de a.
peu importe la valeur de a.
6. Complétion du carré
La méthode de complétion du carré comporte de nombreuses utilités en algèbre, dont la factorisation d’un polynôme quadratique 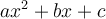 .
.
Si nous voulons factoriser un trinôme général 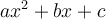 par la méthode présentée précédemment dans cette section, il peut être difficile, même impossible, de trouver les deux nombres dont la somme est
par la méthode présentée précédemment dans cette section, il peut être difficile, même impossible, de trouver les deux nombres dont la somme est 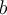 et le produit est
et le produit est 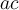 , particulièrement si les deux nombres ne sont pas des entiers. Par exemple, le polynôme
, particulièrement si les deux nombres ne sont pas des entiers. Par exemple, le polynôme 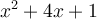 ne se factorise pas par la méthode du trinôme général, car on ne peut pas trouver deux nombres dont la somme est égale à
ne se factorise pas par la méthode du trinôme général, car on ne peut pas trouver deux nombres dont la somme est égale à 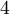 et le produit est égal à
et le produit est égal à  .
.
La méthode de complétion du carré, que nous présenterons à l’aide d’un exemple, permet de déterminer si un trinôme peut être factorisé et, si c’est le cas, de trouver les deux facteurs.
Exemple : Factorisons le polynôme 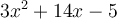 par la complétion du carré.
par la complétion du carré.
1. Mettre en évidence le coefficient 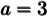
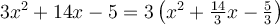
2. Trouver un trinôme carré parfait 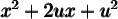 tel que
tel que 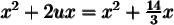
3. Écrire le polynôme initial, si possible, sous la forme d'une différence de carrés 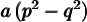
4. Factoriser cette différence de carrés
La factorisation complète du trinôme est donc :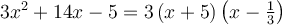 ou
ou 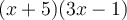 en simplifiant.
en simplifiant.
8. Théorème de la factorisation
Dans certain cas, nous pouvons également utiliser la division polynomiale pour nous aider à factoriser en déterminant auparavant un facteur 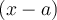 .
.
Afin de trouver ce facteur, il faut appliquer le théorème de la factorisation :
Exemple 1 : Factorisons le polynôme 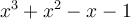 sachant que
sachant que 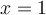 est un zéro du polynôme.
est un zéro du polynôme.
Sachant que 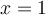 est un zéro de
est un zéro de 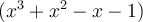 , c'est-à-dire que
, c'est-à-dire que
alors 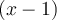 est un facteur linéaire de notre polynôme (de même,
est un facteur linéaire de notre polynôme (de même, 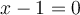 lorsque
lorsque 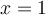 ).
).
Par conséquent, nous pouvons écrire :
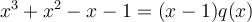
où 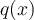 est un polynôme quadratrique de la forme
est un polynôme quadratrique de la forme 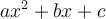
Nous trouvons le trinôme 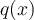 en effectuant la division polynomiale suivante.
en effectuant la division polynomiale suivante.
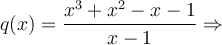 |
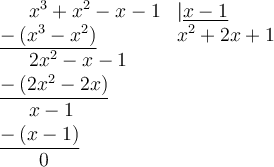 |
Ainsi,
Attention! La factorisation n'est pas terminée, car le facteur quadratique est réductible. On a que
La réponse finale est donc
Exemple 2 : Factorisons le binôme 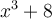 .
.
Cherchons un zéro de 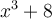 , c'est-à-dire un nombre
, c'est-à-dire un nombre  tel que
tel que 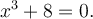
Ce nombre est 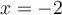 , car
, car 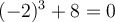 . Par conséquent, le facteur du polynôme
. Par conséquent, le facteur du polynôme 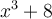 est
est
Nous avons donc
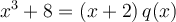 où
où 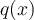 est un polynôme de degré 2.
est un polynôme de degré 2.
Nous trouvons le polynôme 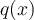 en effectuant une division polynomiale.
en effectuant une division polynomiale.
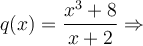 |
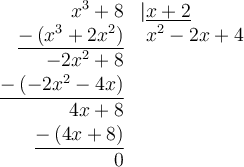 |
Remarque : La factorisation est complète, car le facteur quadratique 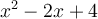 est irréductible puisque son discriminant
est irréductible puisque son discriminant 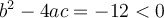 . Nous retrouvons le même résultat que celui obtenu en appliquant la formule de la somme de cubes.
. Nous retrouvons le même résultat que celui obtenu en appliquant la formule de la somme de cubes.
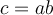

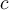
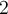
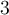
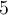
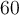
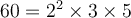
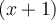
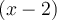
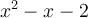
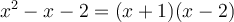
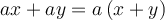
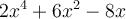
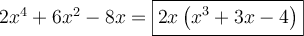
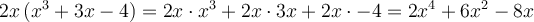
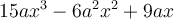
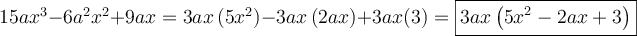
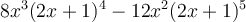
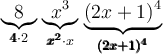
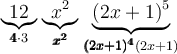
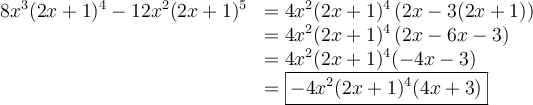
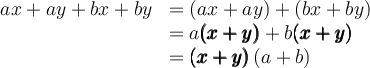
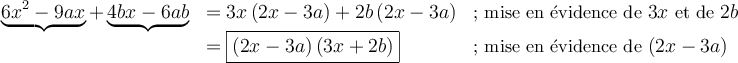
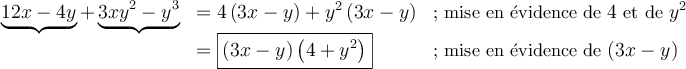
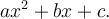
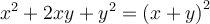
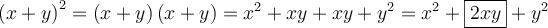
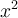
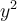
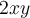
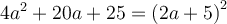
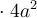
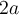
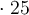
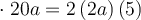
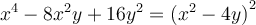
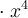
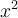
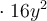
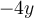
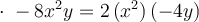
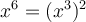
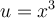
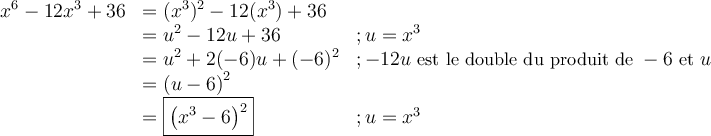
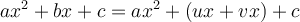
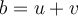

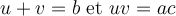
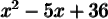
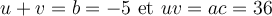
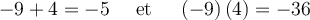
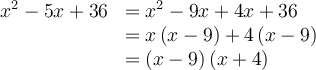
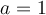
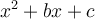
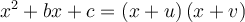
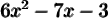
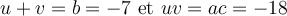
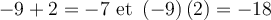
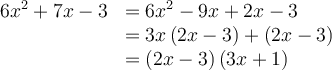
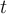
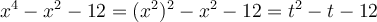
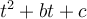
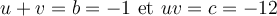
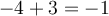
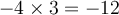
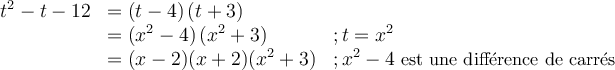
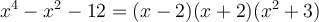
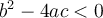
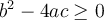
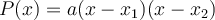
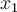
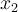
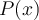
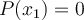
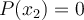
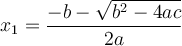
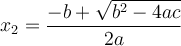
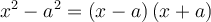
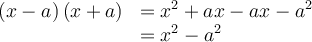
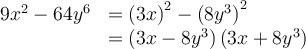
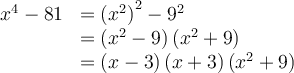
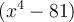
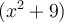
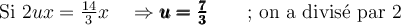
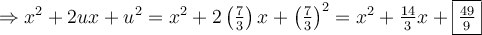
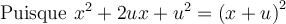
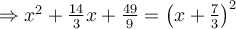
![\begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{x^2} + \frac{14}{3}x - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{x^2} + \frac{14}{3}x + \boxed{\tfrac{49}{9}} - \boxed{\tfrac{49}{9}} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {\left( {{x^2} + \frac{14}{3}x + \frac{49}{9}} \right) - \frac{49}{9} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - \frac{64}{9}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\end{array} \begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{x^2} + \frac{14}{3}x - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{x^2} + \frac{14}{3}x + \boxed{\tfrac{49}{9}} - \boxed{\tfrac{49}{9}} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {\left( {{x^2} + \frac{14}{3}x + \frac{49}{9}} \right) - \frac{49}{9} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - \frac{64}{9}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/38545bb23d30d9621c62137b428a90c1.png)
![\begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{7}{3} + \frac{8}{3}} \right)\left( {x + \frac{7}{3} - \frac{8}{3}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{15}{3}} \right)\left( {x - \frac{1}{3}} \right)}\end{array} \begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{7}{3} + \frac{8}{3}} \right)\left( {x + \frac{7}{3} - \frac{8}{3}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{15}{3}} \right)\left( {x - \frac{1}{3}} \right)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/b04a90577f99aa27000c78e68998b011.png)