1.2 La factorisation
- Introduction
- Mise en évidence simple
- Mise en évidence double
- Trinôme carré parfait
- Trinôme général
- Polynôme quadratique non factorisable
- Différence de deux carrés
- Complétion du carré
- Somme et différence de cubes
- Théorème de la factorisation
6. Complétion du carré
La méthode de complétion du carré comporte de nombreuses utilités en algèbre, dont la factorisation d’un polynôme quadratique 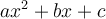 .
.
Si nous voulons factoriser un trinôme général 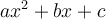 par la méthode présentée précédemment dans cette section, il peut être difficile, même impossible, de trouver les deux nombres dont la somme est
par la méthode présentée précédemment dans cette section, il peut être difficile, même impossible, de trouver les deux nombres dont la somme est 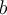 et le produit est
et le produit est 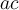 , particulièrement si les deux nombres ne sont pas des entiers. Par exemple, le polynôme
, particulièrement si les deux nombres ne sont pas des entiers. Par exemple, le polynôme 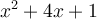 ne se factorise pas par la méthode du trinôme général, car on ne peut pas trouver deux nombres dont la somme est égale à
ne se factorise pas par la méthode du trinôme général, car on ne peut pas trouver deux nombres dont la somme est égale à 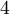 et le produit est égal à
et le produit est égal à  .
.
La méthode de complétion du carré, que nous présenterons à l’aide d’un exemple, permet de déterminer si un trinôme peut être factorisé et, si c’est le cas, de trouver les deux facteurs.
Exemple : Factorisons le polynôme 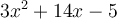 par la complétion du carré.
par la complétion du carré.
1. Mettre en évidence le coefficient 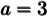
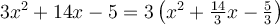
2. Trouver un trinôme carré parfait 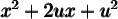 tel que
tel que 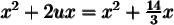
3. Écrire le polynôme initial, si possible, sous la forme d'une différence de carrés 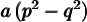
4. Factoriser cette différence de carrés
La factorisation complète du trinôme est donc :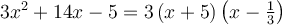 ou
ou 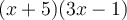 en simplifiant.
en simplifiant.
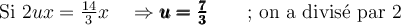
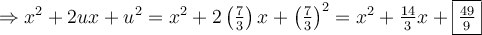
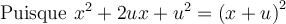
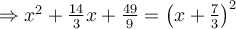
![\begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{x^2} + \frac{14}{3}x - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{x^2} + \frac{14}{3}x + \boxed{\tfrac{49}{9}} - \boxed{\tfrac{49}{9}} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {\left( {{x^2} + \frac{14}{3}x + \frac{49}{9}} \right) - \frac{49}{9} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - \frac{64}{9}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\end{array} \begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{x^2} + \frac{14}{3}x - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{x^2} + \frac{14}{3}x + \boxed{\tfrac{49}{9}} - \boxed{\tfrac{49}{9}} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {\left( {{x^2} + \frac{14}{3}x + \frac{49}{9}} \right) - \frac{49}{9} - \frac{5}{3}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - \frac{64}{9}} \right)}\\[0.5em]{}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/38545bb23d30d9621c62137b428a90c1.png)
![\begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{7}{3} + \frac{8}{3}} \right)\left( {x + \frac{7}{3} - \frac{8}{3}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{15}{3}} \right)\left( {x - \frac{1}{3}} \right)}\end{array} \begin{array}{rl}{3{x^2} + 14x - 5}&{ = 3\left( {{{\left( {x + \frac{7}{3}} \right)}^2} - {{\left( {\frac{8}{3}} \right)}^2}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{7}{3} + \frac{8}{3}} \right)\left( {x + \frac{7}{3} - \frac{8}{3}} \right)}\\[0.5em]{}&{ = 3\left( {x + \frac{15}{3}} \right)\left( {x - \frac{1}{3}} \right)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/b04a90577f99aa27000c78e68998b011.png)