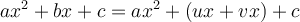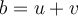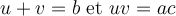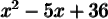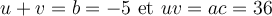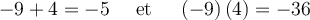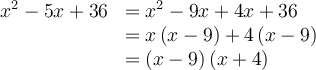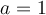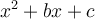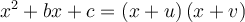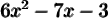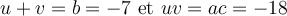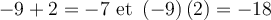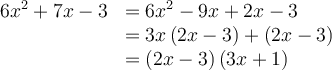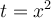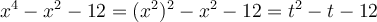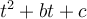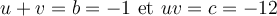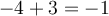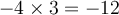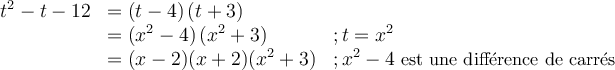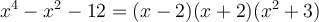1.2 La factorisation
- Introduction
- Mise en évidence simple
- Mise en évidence double
- Trinôme carré parfait
- Trinôme général
- Polynôme quadratique non factorisable
- Différence de deux carrés
- Complétion du carré
- Somme et différence de cubes
- Théorème de la factorisation
4. Polynômes quadratiques
4.2. Trinôme général
où
et 
On peut factoriser un trinôme général en suivant les étapes suivantes :
1. On cherche deux nombres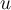 
et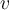 
, dont la somme est 
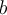et le produit est 
.
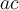2. On remplace 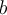par la somme de ces deux nombres.
3. On effectue une mise en évidence double.
Exemples : Factorisons les trinômes suivants.
a)
On cherche deux nombres tels que
On effectue ensuite une double mise en évidence de la façon suivante :
Remarque : Si 
, le trinôme de la forme 
peut se factoriser plus directement de la façon suivante :
b)
On cherche deux nombres tels que
On effectue ensuite une double mise en évidence :
c)
Tout d'abord, remarquons que 
. Remplaçons 
afin d'exprimer notre polynôme en 
de degré 4 en un polynôme en 
de degré 2. Nous obtenons
Notre polynôme est maintenant sous la forme 
. Pour le factoriser, on cherche deux nombres tels que
On a 
et 
.
On obtient alors :
Par conséquent, 
.