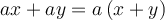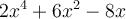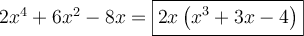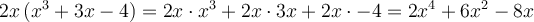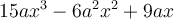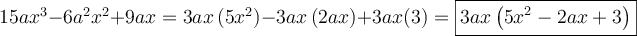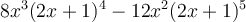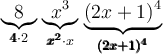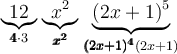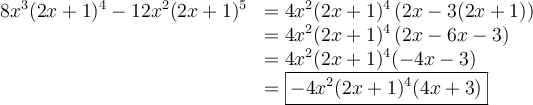1.2 La factorisation
- Introduction
- Mise en évidence simple
- Mise en évidence double
- Trinôme carré parfait
- Trinôme général
- Polynôme quadratique non factorisable
- Différence de deux carrés
- Complétion du carré
- Somme et différence de cubes
- Théorème de la factorisation
2. Mise en évidence simple
La méthode de mise en évidence simple est utilisée lorsque tous les termes du polynôme contiennent un facteur commun. On se souvient que les termes dans une expression sont séparés par une addition ou une soustraction. Pour mettre en évidence ce facteur commun, on utilise la propriété de la distributivité de la multiplication sur l’addition :
Exemples : Factoriser les expressions suivantes.
Ce polynôme contient 3 termes et chacun des termes a 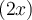 comme facteur commun:
comme facteur commun:
On remarque qu'en effectuant une distributivité sur la réponse, on revient à l'expression de départ :
Ce polynôme à deux variables contient également 3 termes et chacun a 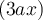 comme facteur commun :
comme facteur commun :
Cette expression contient seulement 2 termes, 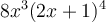 et
et 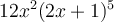 , qui sont séparés par une soustraction. Chacun des termes possèdent trois facteurs : une constante, une puissance de
, qui sont séparés par une soustraction. Chacun des termes possèdent trois facteurs : une constante, une puissance de  et une puissance de
et une puissance de 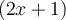 . Trouvons les facteurs communs :
. Trouvons les facteurs communs :
Les facteurs communs sont ceux en gras sous chacun des termes, alors en mettant en évidence ces facteurs on obtient :