3.3 Fonctions trigonométriques inverses
- Introduction
- Fonction arcsin
- Fonction arccos
- Fonction arctan
- Autres fonctions trigonométriques inverses
- Résoudre une équation trigonométrique
6. Résoudre une équation trigonométrique
Résoudre une équation contenant des fonctions trigonométriques signifie trouver l'angle qui vérifie cette équation dans les restrictions données. Nous avons fait quelques exemples de ce type de problème dans les sections précédentes. Nous allons voir dans la présente section d'autres situations où il faut déterminer la valeur d'un angle.
Voici quelques étapes qui nous aideront dans notre résolution.
- Déterminer le domaine de l'équation et les restrictions.
-
Transformer l'équation en une ou plusieurs équations équivalentes de la forme
Vous pouvez utiliser les définitions des rapports trigonométriques, ainsi que les identités afin de transformer votre équation.
- Chercher sur le cercle trigonométrique les angles
 correspondant aux valeurs de sinus ou cosinus et respectant le domaine de l'équation.
correspondant aux valeurs de sinus ou cosinus et respectant le domaine de l'équation.
Exemples : Résoudre les équations suivantes.
Solution
- Le domaine de cette équation est
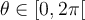 et il n'y a aucune restriction pour sinus.
et il n'y a aucune restriction pour sinus. 
Isolons la fonction sinus :
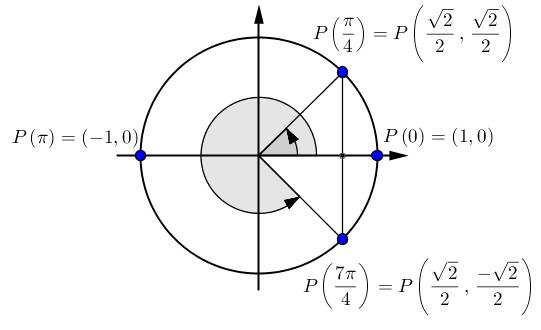
- Sur le cercle trigonométrique, on a
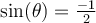 si
si 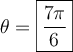 et
et 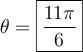 . Ces deux valeurs font partie du domaine.
. Ces deux valeurs font partie du domaine.
Solution On transforme tout d'abord le membre de droite pour obtenir des sinus et cosinus.
- Sur l'intervalle
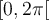 , il y a deux restrictions :
, il y a deux restrictions : 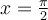 et
et 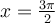 , car, pour ces deux valeurs, le dénominateur
, car, pour ces deux valeurs, le dénominateur 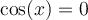 .
. -
Simplifions cette équation.
Ainsi, chacun des facteurs de cette dernière équation peut être égal à 0. C'est-à-dire
Pour l'équation (1), les valeurs de l'angle
 pour lesquelles
pour lesquelles 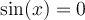 sont
sont  et
et 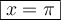 .
.Pour l'équation (2), on trouve sur le cercle trigonométrique les valeurs de l'angle
 pour lesquelles
pour lesquelles 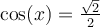 . Soit
. Soit
Ces quatre solutions font partie du domaine de l'équation et respectent les restrictions.
Exemple : Déterminer le domaine de la fonction 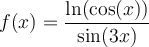 .
.
Solution Le domaine de cette fonction dépend des restrictions suivantes :
-
La fonction logarithmique ln est définie pour des arguments strictement positifs (> 0). Par conséquent, il faut que son argument
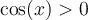 .
.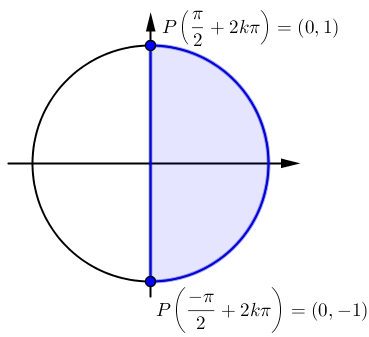
On trouve sur le cercle trigonométrique que les valeurs de l'angle
 pour lesquelles la valeur de cosinus est strictement positive sont
pour lesquelles la valeur de cosinus est strictement positive sont ![\left]\frac{-\pi}{2},\frac{\pi}{2}\right[ \left]\frac{-\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7a3a937ab84dac291b827974ef47af89.png) .
.Par contre, on sait également qu'en faisant des tours complets sur le cercle, il existe d'autres valeurs
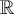 pour lesquelles cosinus est
pour lesquelles cosinus est 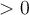 . Étant donné que
. Étant donné que -
La deuxième restriction est que le dénominateur doit être non nul. Par conséquent, il faut que
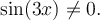
On a que
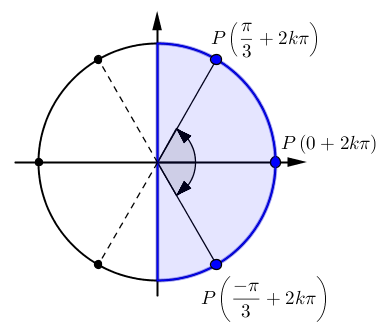
En situant les valeurs où
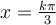 sur le cercle trigonométrique, on constate que seulement trois points font partie de l'intervalle de la restriction précédente :
sur le cercle trigonométrique, on constate que seulement trois points font partie de l'intervalle de la restriction précédente :Il faut donc exclure du domaine de
 ces valeurs de
ces valeurs de  pour lesquelles
pour lesquelles 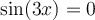 et qui se trouvent dans l'intervalle
et qui se trouvent dans l'intervalle ![x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[. x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[.](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/00bcc3627b91eb0e653741d68125be3d.png)
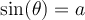
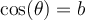
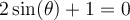
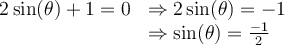
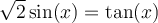
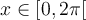
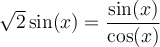
![\begin{array}{rll}\sqrt{2}\sin(x)&=\dfrac{\sin(x)}{\cos(x)}&\\[1em]\sqrt{2}\sin(x)\cos(x)&=\sin(x)&\small\text{; on a multiplié chaque}\\&&\small\text{ membre par }\cos(x)\\\sqrt{2}\sin(x)\cos(x)-\sin(x)&=0&\\[1em]\underset{(1)}{\underbrace{\sin(x)}}\underset{(2)}{\underbrace{\left(\sqrt{2}\cos(x)-1\right)}}&=0&\small\text{; on a factorisé}\end{array} \begin{array}{rll}\sqrt{2}\sin(x)&=\dfrac{\sin(x)}{\cos(x)}&\\[1em]\sqrt{2}\sin(x)\cos(x)&=\sin(x)&\small\text{; on a multiplié chaque}\\&&\small\text{ membre par }\cos(x)\\\sqrt{2}\sin(x)\cos(x)-\sin(x)&=0&\\[1em]\underset{(1)}{\underbrace{\sin(x)}}\underset{(2)}{\underbrace{\left(\sqrt{2}\cos(x)-1\right)}}&=0&\small\text{; on a factorisé}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2fda081a813fbf3567e6baa15955e4af.png)
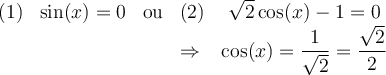
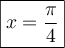
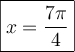
![\begin{array}{rl}P\left(\frac{-\pi}{2}\right)&=P\left(\frac{-\pi}{2}+2k\pi\right)\\[1em]\text{et }P\left(\frac{\pi}{2}\right)&=P\left(\frac{\pi}{2}+2k\pi\right)\end{array} \begin{array}{rl}P\left(\frac{-\pi}{2}\right)&=P\left(\frac{-\pi}{2}+2k\pi\right)\\[1em]\text{et }P\left(\frac{\pi}{2}\right)&=P\left(\frac{\pi}{2}+2k\pi\right)\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9afc16ee56da2ba8e3eac9987fc6cd7b.png)
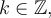
![x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[ x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/01a92d51c8a6652c32afb757807ce9aa.png)
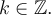
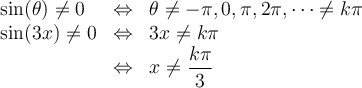
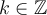
![\begin{array}{rl}P\left(\frac{-\pi}{3}\right)&=P\left(\frac{-\pi}{3}+2k\pi\right)\\[1em]P(0)&=P(2k\pi)\\[1em]P\left(\frac{\pi}{3}\right)&=P\left(\frac{\pi}{3}+2k\pi\right)\end{array} \begin{array}{rl}P\left(\frac{-\pi}{3}\right)&=P\left(\frac{-\pi}{3}+2k\pi\right)\\[1em]P(0)&=P(2k\pi)\\[1em]P\left(\frac{\pi}{3}\right)&=P\left(\frac{\pi}{3}+2k\pi\right)\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/37f05ce0b84e4a49ec34bbfe544ecb2c.png)
![\text{dom}\left(\frac{\ln(\cos(x))}{\sin(3x)}\right)=x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[\setminus\left\lbrace\frac{-\pi}{3}+2k\pi, 2k\pi,\frac{\pi}{3}+2k\pi\right\rbrace \text{dom}\left(\frac{\ln(\cos(x))}{\sin(3x)}\right)=x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[\setminus\left\lbrace\frac{-\pi}{3}+2k\pi, 2k\pi,\frac{\pi}{3}+2k\pi\right\rbrace](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c04a95e3a526250c513de5fa8f0c0ece.png)