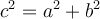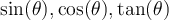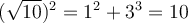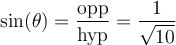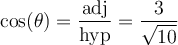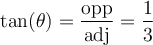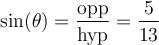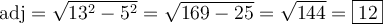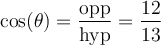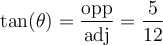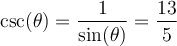3.1 La trigonométrie
- Définitions
- Angles remarquables
- Angles : degré et radian
- Cercle trigonométrique
- Fonctions trigonométriques et leur domaine
- Graphes des fonctions trigonométriques
1. Définitions
Considérons le triangle rectangle
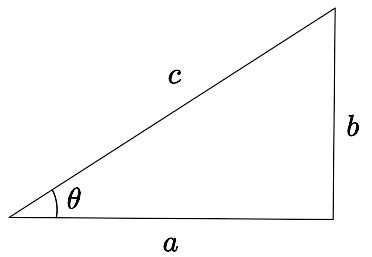
Nous appellerons hypoténuse le côté opposé à l'angle droit. Dans l'image ci-haut, l'hypoténuse est désignée par 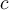 .
.
Évidemment, pour un angle  donné, les longueurs des différents côtés ne sont pas fixées. En effet, on peut construire des triangles semblables en allongeant les différents côtés d'un même facteur.
donné, les longueurs des différents côtés ne sont pas fixées. En effet, on peut construire des triangles semblables en allongeant les différents côtés d'un même facteur.
Nous pouvons créer un lien entre les longueurs des côtés du triangle rectangle par le théorème de Pythagore :
De plus, nous pouvons aussi dire que les rapports entre les côtés restent les mêmes pour un angle  fixé. Ce sont ces rapports qui forment les fonctions trigonométriques. Par exemple, dans le graphique Geogebra suivant,
fixé. Ce sont ces rapports qui forment les fonctions trigonométriques. Par exemple, dans le graphique Geogebra suivant, ![]() déplacez le point A sur le côté adjacent à l'angle
déplacez le point A sur le côté adjacent à l'angle  . On remarque que le rapport
. On remarque que le rapport 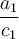 est constant pour un angle
est constant pour un angle  fixe, de même que tous les autres rapports.
fixe, de même que tous les autres rapports.
On peut donc nommer ces rapports et définir des fonctions qui associent, pour un angle donné, un des rapports du triangle.
Nous désignerons par opp le côté opposé à l'angle et par adj le côté adjacent. Dans le triangle illustré, 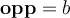 et
et 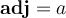 .
.
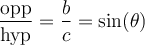 |
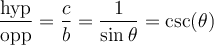 |
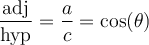 |
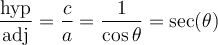 |
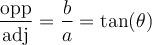 |
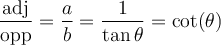 |
Exemples :
a) À l'aide du triangle,
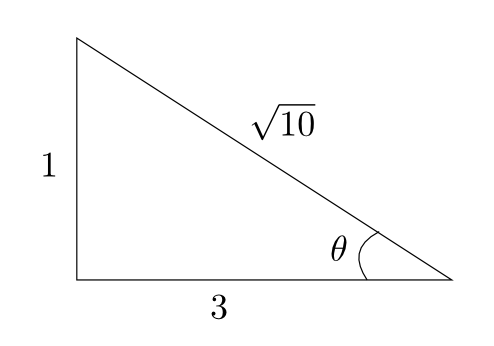
solution En localisant la position de l'angle  et l'angle droit du triangle, on obtient que
et l'angle droit du triangle, on obtient que
la mesure de l'hypothénuse vaut 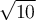 unités
unités
la mesure du côté opposé à  vaut
vaut  unité
unité
la mesure du côté adjacent à  vaut
vaut 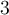 unités.
unités.
On remarque que les longueurs des côtés respectent le théorème de Pythagore, car :
On peut maintenant calculer les rapports demandés :
b) Sachant que 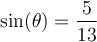 pour
pour ![\theta\in\left[0, \pi/2 \right] \theta\in\left[0, \pi/2 \right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9336d5f6466598171129108422fef606.png) , déterminer les valeurs de
, déterminer les valeurs de 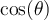 ,
, 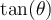 et
et 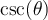 .
.
solution On sait que pour tout angle  , la fonction sinus est le rapport constant
, la fonction sinus est le rapport constant 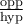 . Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
. Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
Ainsi le côté opposé à l'angle mesure 5 unités et l'hypoténuse mesure 13 unités. Par le théorème de Pythagore, nous trouvons que la mesure du côté adjacent à l'angle vaut :

Étant donné que l'angle  prend des valeurs entre 0 et
prend des valeurs entre 0 et 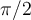 , nous savons que les valeurs des fonctions trigonométriques sont toutes positives. Ainsi, en lisant le triangle rectangle, on peut calculer les rapports demandés.
, nous savons que les valeurs des fonctions trigonométriques sont toutes positives. Ainsi, en lisant le triangle rectangle, on peut calculer les rapports demandés.