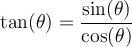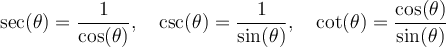3.1 La trigonométrie
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 3.1 La trigonométrie |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 05:30 |
Description
- Définitions
- Angles remarquables
- Angles : degré et radian
- Cercle trigonométrique
- Fonctions trigonométriques et leur domaine
- Graphes des fonctions trigonométriques
1. Définitions
Considérons le triangle rectangle
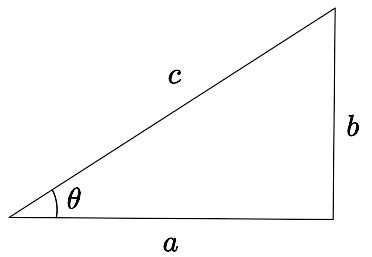
Nous appellerons hypoténuse le côté opposé à l'angle droit. Dans l'image ci-haut, l'hypoténuse est désignée par 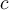 .
.
Évidemment, pour un angle  donné, les longueurs des différents côtés ne sont pas fixées. En effet, on peut construire des triangles semblables en allongeant les différents côtés d'un même facteur.
donné, les longueurs des différents côtés ne sont pas fixées. En effet, on peut construire des triangles semblables en allongeant les différents côtés d'un même facteur.
Nous pouvons créer un lien entre les longueurs des côtés du triangle rectangle par le théorème de Pythagore :
De plus, nous pouvons aussi dire que les rapports entre les côtés restent les mêmes pour un angle  fixé. Ce sont ces rapports qui forment les fonctions trigonométriques. Par exemple, dans le graphique Geogebra suivant,
fixé. Ce sont ces rapports qui forment les fonctions trigonométriques. Par exemple, dans le graphique Geogebra suivant, ![]() déplacez le point A sur le côté adjacent à l'angle
déplacez le point A sur le côté adjacent à l'angle  . On remarque que le rapport
. On remarque que le rapport 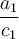 est constant pour un angle
est constant pour un angle  fixe, de même que tous les autres rapports.
fixe, de même que tous les autres rapports.
On peut donc nommer ces rapports et définir des fonctions qui associent, pour un angle donné, un des rapports du triangle.
Nous désignerons par opp le côté opposé à l'angle et par adj le côté adjacent. Dans le triangle illustré, 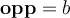 et
et 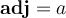 .
.
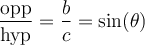 |
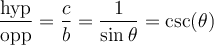 |
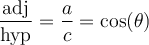 |
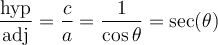 |
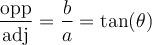 |
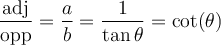 |
Exemples :
a) À l'aide du triangle,
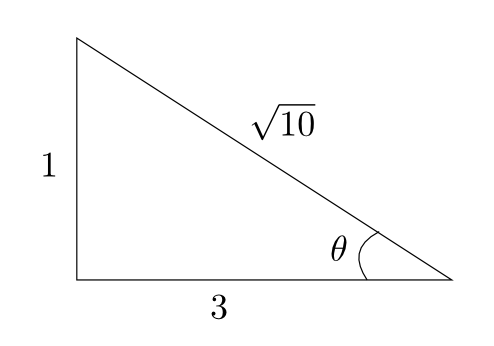
solution En localisant la position de l'angle  et l'angle droit du triangle, on obtient que
et l'angle droit du triangle, on obtient que
la mesure de l'hypothénuse vaut 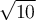 unités
unités
la mesure du côté opposé à  vaut
vaut  unité
unité
la mesure du côté adjacent à  vaut
vaut 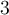 unités.
unités.
On remarque que les longueurs des côtés respectent le théorème de Pythagore, car :
On peut maintenant calculer les rapports demandés :
b) Sachant que 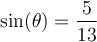 pour
pour ![\theta\in\left[0, \pi/2 \right] \theta\in\left[0, \pi/2 \right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9336d5f6466598171129108422fef606.png) , déterminer les valeurs de
, déterminer les valeurs de 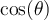 ,
, 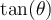 et
et 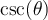 .
.
solution On sait que pour tout angle  , la fonction sinus est le rapport constant
, la fonction sinus est le rapport constant 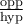 . Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
. Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
Ainsi le côté opposé à l'angle mesure 5 unités et l'hypoténuse mesure 13 unités. Par le théorème de Pythagore, nous trouvons que la mesure du côté adjacent à l'angle vaut :

Étant donné que l'angle  prend des valeurs entre 0 et
prend des valeurs entre 0 et 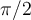 , nous savons que les valeurs des fonctions trigonométriques sont toutes positives. Ainsi, en lisant le triangle rectangle, on peut calculer les rapports demandés.
, nous savons que les valeurs des fonctions trigonométriques sont toutes positives. Ainsi, en lisant le triangle rectangle, on peut calculer les rapports demandés.
2. Angles remarquables
Trois angles particuliers
Construisons un triangle rectangle isocèle, c'est-à-dire avec deux côtés égaux, et avec une hypoténuse de 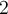 . Les 2 angles autres que l'angle droit sont égaux et mesurent donc
. Les 2 angles autres que l'angle droit sont égaux et mesurent donc 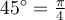 .
.
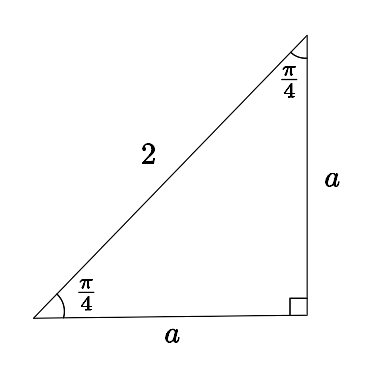
Dans ce cas, puisque les deux côtés sont égaux, on a, par Pythagore,
Comme le triangle est construit au complet, on peut déduire les valeurs des fonctions trigonométriques. Par exemple,
Cas (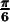 ou 30 degrés) et (
ou 30 degrés) et (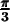 ou 60 degrés)
ou 60 degrés)
Considérons maintenant un triangle équilatéral de côtés  . Traçons la bissectrice à partir du sommet du haut. Nous obtenons le triangle
. Traçons la bissectrice à partir du sommet du haut. Nous obtenons le triangle
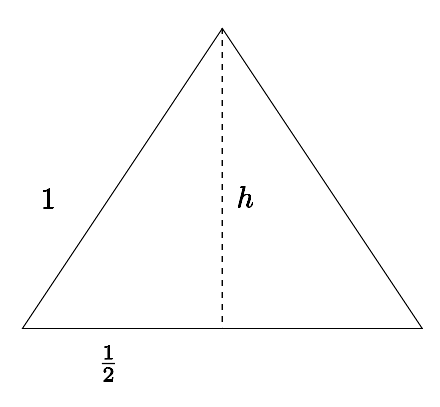
Cette bissectrice est aussi la médiatrice, car le triangle est équilatéral. Encore une fois, par Pythagore, on peut déduire que
Puisque le triangle équilatéral a 3 angles égaux (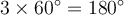 ) et que la bissectrice en coupe un en deux, on obtient le triangle
) et que la bissectrice en coupe un en deux, on obtient le triangle
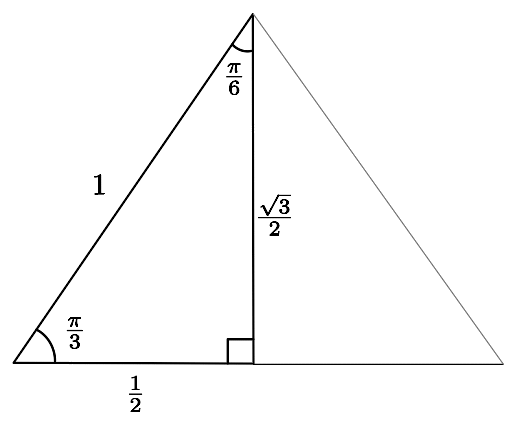
Il ne reste qu'à lire le triangle
3. Angles : degré et radian
Lorsqu'on mesure les angles dans un cercle, par convention, le zéro est situé à droite à l'horizontale et on augmente dans le sens antihoraire tel qu'illustré dans la figure ci-dessous. Dans ce cas, la mesure de l'angle est positive, et elle est négative si la rotation se fait dans le sens horaire.
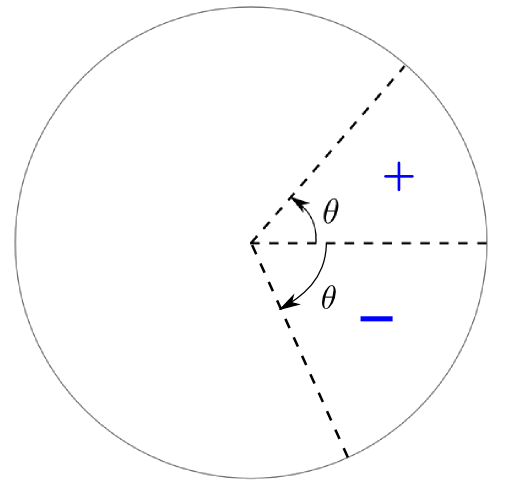
Deux façons de diviser le cercle sont largement répandues : les degrés et les radians.
Les degrés
Dans le système de degré, on divise le cercle en 360 parties égales. Chacune de ces parties mesure 1 degré. Dans ce système, un angle droit mesure 90 degrés.
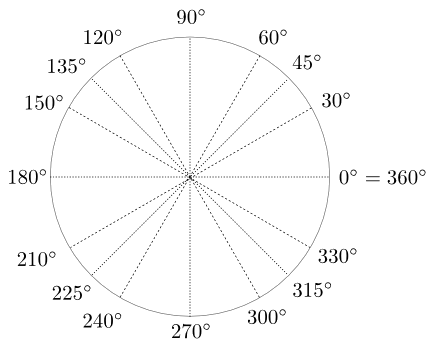
Les radians
Dans le système de radians, on mesure la longueur de la corde associée à l'angle en question dans un cercle de rayon 1. On a alors qu'un angle faisant un tour complet du cercle mesure 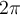 radians. L’intérêt majeur de ce système de mesure d'angle est de rattacher la mesure à un concept de longueur de la corde. Les principaux angles en radians sont
radians. L’intérêt majeur de ce système de mesure d'angle est de rattacher la mesure à un concept de longueur de la corde. Les principaux angles en radians sont
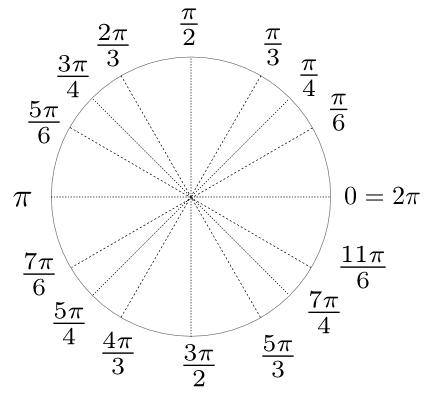
Le graphique Geogebra suivant explique de façon dynamique la notion d'angle en radian.
![]() Déplacez le point P sur le cercle de rayon 1. L'angle en radian correspond à la mesure de l'arc en bleu sur le cercle. Par exemple, si P fait un angle de
Déplacez le point P sur le cercle de rayon 1. L'angle en radian correspond à la mesure de l'arc en bleu sur le cercle. Par exemple, si P fait un angle de 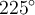 , alors la longueur de l'arc en bleu est d'environ
, alors la longueur de l'arc en bleu est d'environ 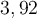 radians, soit
radians, soit 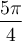 radians.
radians.
En continuant à déplacer le point P sur le cercle, vous passez sur les points ![]() correspondant aux différents angles remarquables et leurs équivalences en degrés et en radians.
correspondant aux différents angles remarquables et leurs équivalences en degrés et en radians.
Passer des radians aux degrés et vice versa
Pour passer d'un système de mesure à l'autre, il suffit d'effectuer une règle de 3. En effet, il y a un rapport de proportionnalité entre les radians et les degrés. Ainsi, puisque 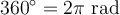
Par exemple, pour un angle 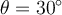 , on a que
, on a que 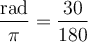 et donc
et donc 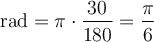
Les points trigonométriques égaux
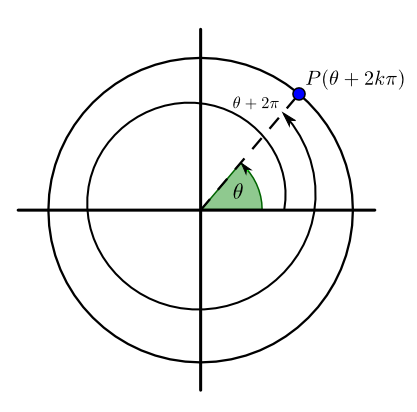
On constate qu'en partant d'un point sur le cercle et en effectuant des tours complets, on revient toujours au même point. Faire un tour complet signifie ajouter à un angle un multiple de 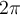 , ou
, ou 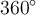 .
.
On en déduit le résultat suivant :
Exercices formatifs WeBWorK
 La trigonométrie et les angles
La trigonométrie et les angles
4. Cercle trigonométrique
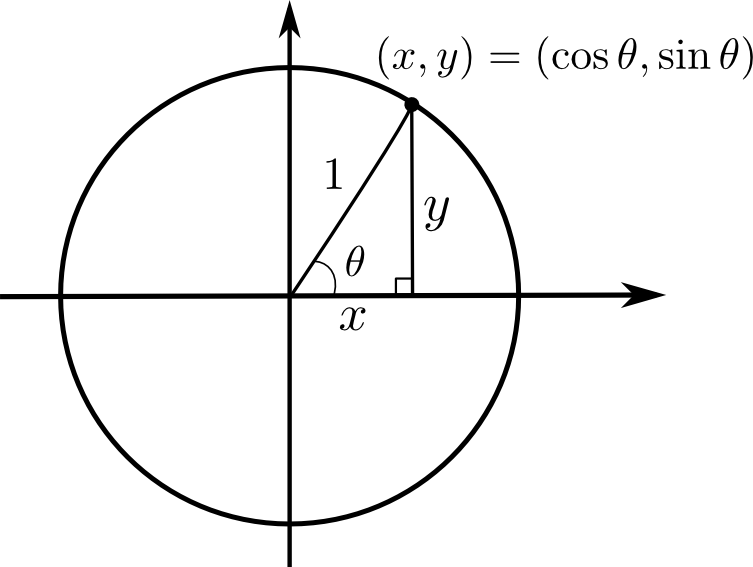
Considérons un cercle de rayon 1 et un point 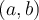 de ce cercle. Si le point est situé dans le premier quadrant, il détermine un triangle rectangle.
de ce cercle. Si le point est situé dans le premier quadrant, il détermine un triangle rectangle.
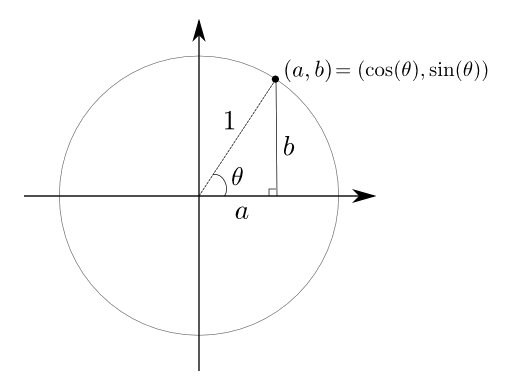
Étant donné ce que nous avons vu sur la trigonométrie dans le triangle, puisque l'hypoténuse mesure  unité, on déduit que
unité, on déduit que
c'est-à-dire que la première coordonnée correspond au cosinus de l'angle et la deuxième, au sinus. On va étendre les définitions des fonctions trigonométriques en posant que 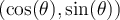 sont les coordonnées sur le cercle du point engendré par un angle de
sont les coordonnées sur le cercle du point engendré par un angle de  . De cette façon, on peut déduire les valeurs des angles remarquables en procédant par symétrie.
. De cette façon, on peut déduire les valeurs des angles remarquables en procédant par symétrie.
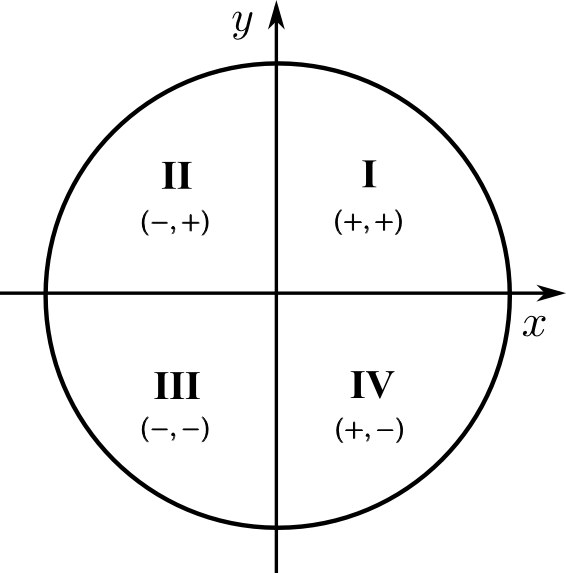
Les signes du sinus de  et du cosinus de
et du cosinus de  sont déterminés par la position du point sur le cercle, plus précisément par le quadrant dans lequel ce point est situé.
sont déterminés par la position du point sur le cercle, plus précisément par le quadrant dans lequel ce point est situé.
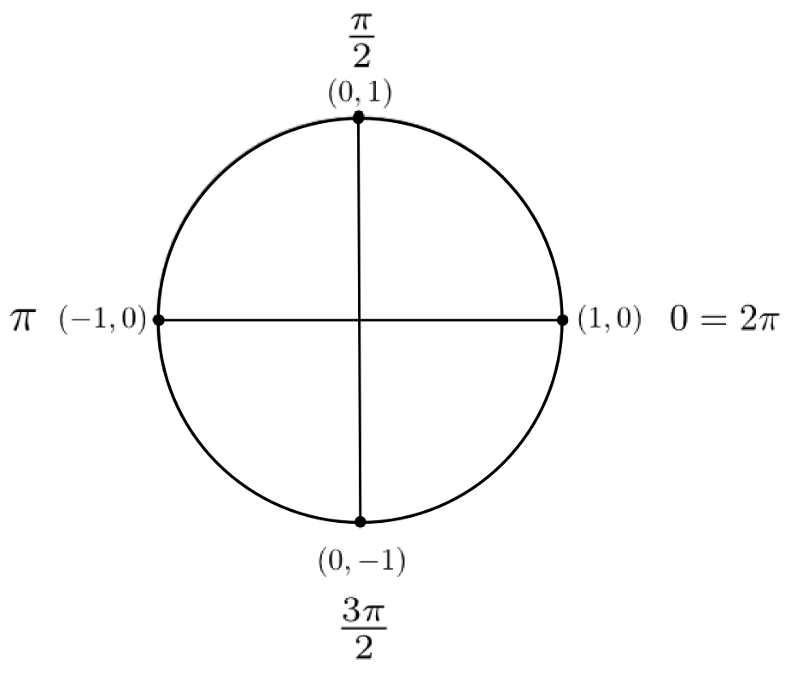
Tout d'abord, puisque le cercle est de rayon 1, il est facile de déduire qu'il coupe les axes aux coordonnées
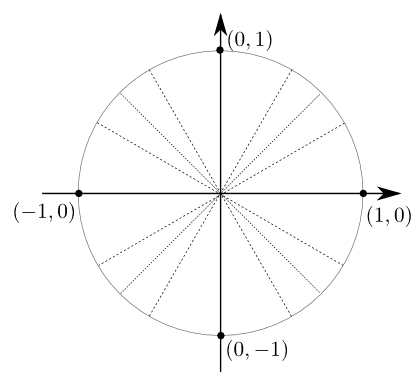
Ces points correspondent aux angles suivants en radians.
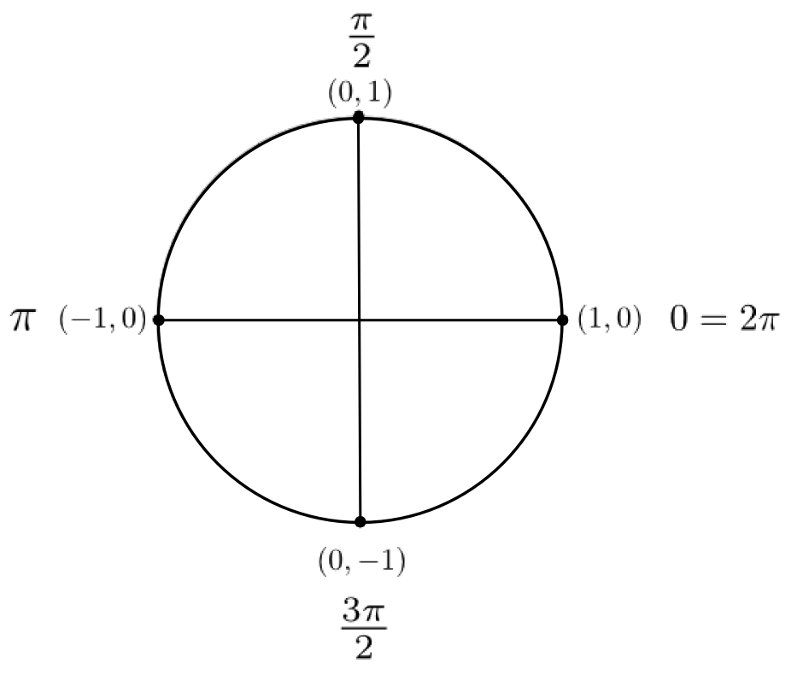
Étant donné ce que nous avons calculé précédemment dans la trigonométrie du triangle, on peut déduire les valeurs suivantes. En effet, la première coordonnée correspond au cosinus et la deuxième, au sinus de l'angle en question.
 |
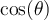 |
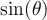 |
 ou ou 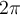 |
 |
 |
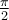 |
 |
 |
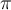 |
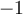 |
 |
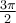 |
 |
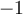 |
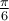 |
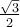 |
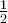 |
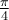 |
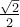 |
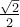 |
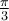 |
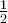 |
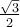 |
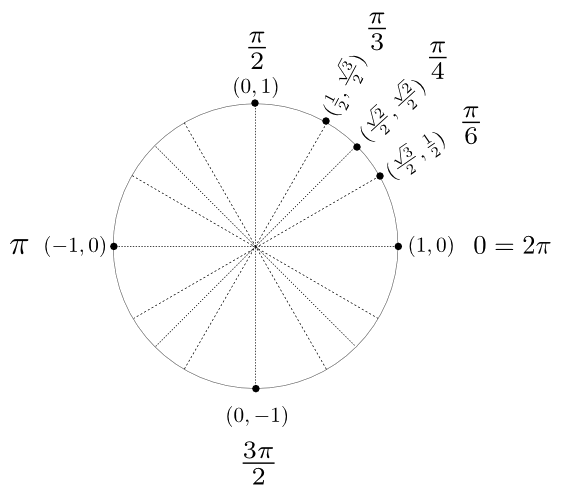
Par la suite, en procédant par symétrie, on peut déduire l'ensemble des valeurs particulières du cercle trigonométrique.
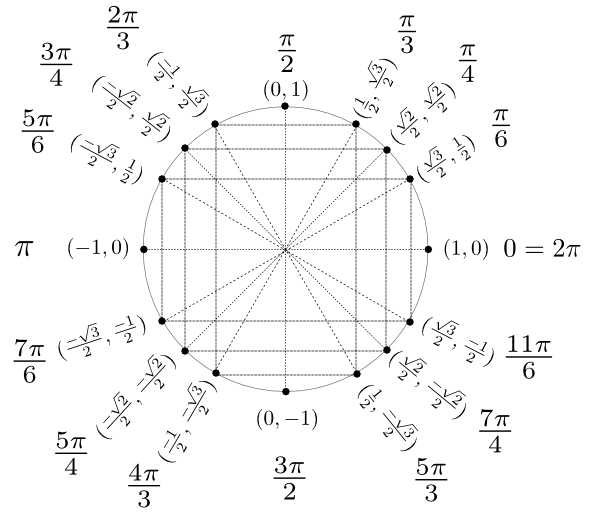
Exemple : Calculons les coordonnées du point P situé à un angle 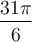 radians sur le cercle trigonométrique.
radians sur le cercle trigonométrique.
solution Chaque tour de cercle dans le sens antihoraire correspond à un angle de 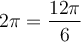 . Par conséquent,
. Par conséquent,
Les coordonnées du point 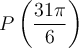 sont les mêmes que celles du point
sont les mêmes que celles du point 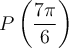 , soit
, soit 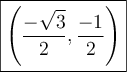 .
.
Exemple : Sachant que 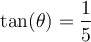 pour
pour ![\theta\in\left[0, 2\pi \right] \theta\in\left[0, 2\pi \right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f8b5d3fbb3b4eb2a7ec3b6cd20f8108e.png) , déterminer les valeurs de
, déterminer les valeurs de 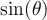 et
et 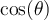 .
.
solution On sait que pour tout angle  , la fonction tangente est le rapport constant
, la fonction tangente est le rapport constant 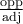 .
. Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
Par conséquent, nous allons créer un triangle rectangle respectant ce rapport trigonométrique,
Ainsi le côté opposé à l'angle est 1 et le côté adjacent est 5. Par le théorème de Pythagore, nous trouvons l'hypoténuse :
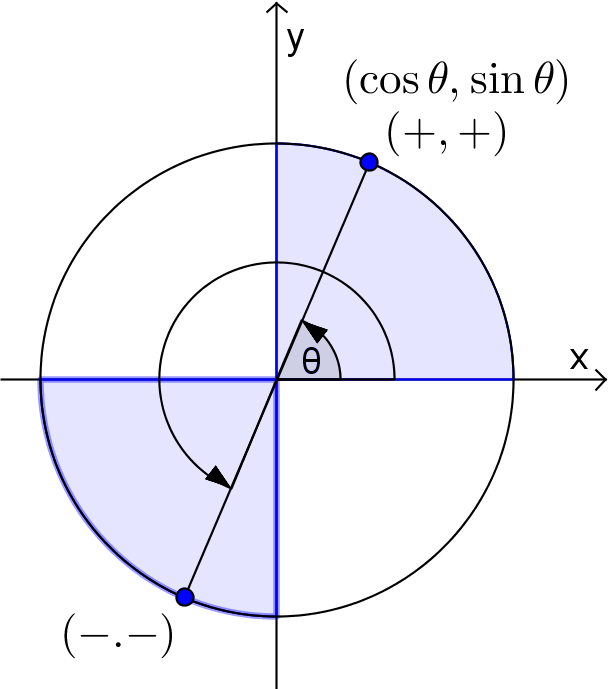
Étant donné que l'angle  prend des valeurs entre
prend des valeurs entre  et
et 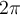 , les valeurs de
, les valeurs de 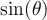 et
et 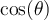 sont déterminées par les coordonnées des points sur le cercle situés dans le premier quadrant
sont déterminées par les coordonnées des points sur le cercle situés dans le premier quadrant 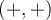 ou le troisième quadrant
ou le troisième quadrant 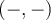 . En effet,
. En effet,
Ainsi, en lisant le triangle rectangle, on peut calculer les rapports demandés.
Exercices formatifs WeBWorK
 Cercle trigonométrique
Cercle trigonométrique
5. Fonctions trigonométriques et leur domaine
En utilisant ce que nous avons vu dans la section précédente, on définit les fonctions trigonométriques de la façon suivante.
Lorsque l'angle se situe entre  et
et 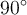 , le point est situé dans le premier quadrant et les définitions précédentes coïncident avec celles que nous avions données dans la section sur la trigonométrie du triangle.
, le point est situé dans le premier quadrant et les définitions précédentes coïncident avec celles que nous avions données dans la section sur la trigonométrie du triangle.
Recherche des domaines
Le domaine des fonctions sinus et cosinus est l'ensemble des 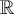 , car pour tout nombre réel
, car pour tout nombre réel  , les valeurs
, les valeurs 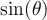 et
et 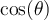 sont définies.
sont définies.
Par contre, il en est tout autre pour les valeurs de 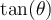 ,
, 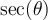 ,
, 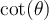 et
et 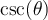 , car on peut voir dans le tableau ci-dessus que ces expressions sont définies uniquement si leur dénominateur n'est pas égal à 0. Il est donc très utile de connaître les angles
, car on peut voir dans le tableau ci-dessus que ces expressions sont définies uniquement si leur dénominateur n'est pas égal à 0. Il est donc très utile de connaître les angles  où les valeurs
où les valeurs 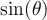 et
et 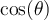 sont égales à 0. En fait, ces angles
sont égales à 0. En fait, ces angles  sont ceux qui engendrent les points qui croisent les axes de coordonnées sur le cercle trigonométrique.
sont ceux qui engendrent les points qui croisent les axes de coordonnées sur le cercle trigonométrique.
La dernière ligne de chacun des tableaux indique que tous les angles qui annulent le cosinus ou le sinus sont nuls sont séparés par un angle de 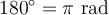 . On en déduit les domaines des autres fonctions trigonométriques.
. On en déduit les domaines des autres fonctions trigonométriques.
Exemples :
a) Trouver le domaine de la fonction 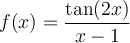 .
.
solution Réécrivons  en fonction de sinus et cosinus.
en fonction de sinus et cosinus.
Pour que  soit définie, il faut que le dénominateur soit
soit définie, il faut que le dénominateur soit 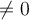 . On a que
. On a que
Par conséquent, le domaine de 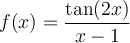 est :
est :
b) Trouver le domaine de la fonction 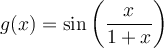
solution Il s'agit d'une fonction composée et son domaine dépend du domaine de 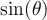 où
où 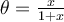 et du domaine de la fonction
et du domaine de la fonction 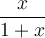 .
.
6. Graphes des fonctions trigonométriques
On peut représenter les différentes fonctions trigonométriques par un graphique en utilisant l'angle  comme abscisse et la valeur de la fonction trigonométrique comme ordonnée. Nous allons d'abord nous intéresser aux cas des fonctions sinus et cosinus.
comme abscisse et la valeur de la fonction trigonométrique comme ordonnée. Nous allons d'abord nous intéresser aux cas des fonctions sinus et cosinus.
Le sinus est obtenu en considérant l'ordonnée du point engendré par un angle  sur un cercle de rayon 1. Dans le graphe ci-dessous, vous pouvez
sur un cercle de rayon 1. Dans le graphe ci-dessous, vous pouvez ![]() déplacer ce point sur la courbe de
déplacer ce point sur la courbe de 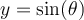 à l'aide du curseur ou cliquer sur
à l'aide du curseur ou cliquer sur ![]() pour lancer l'animation. L'ordonnée du point P sur le cercle de droite, représentée par le segment bleu, varie en fonction de l'angle et est égal à la valeur de
pour lancer l'animation. L'ordonnée du point P sur le cercle de droite, représentée par le segment bleu, varie en fonction de l'angle et est égal à la valeur de 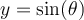 .
.
Le cosinus est quant à lui obtenu en considérant l'abscisse du point engendré par un angle  sur un cercle de rayon 1. Dans le graphe ci-dessous, vous pouvez
sur un cercle de rayon 1. Dans le graphe ci-dessous, vous pouvez ![]() déplacer ce point sur la courbe de
déplacer ce point sur la courbe de 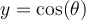 à l'aide du curseur ou cliquer sur
à l'aide du curseur ou cliquer sur ![]() pour lancer l'animation. L'abscisse du point P sur le cercle de droite, représentée par le segment mauve, varie en fonction de l'angle et est égal à la valeur de
pour lancer l'animation. L'abscisse du point P sur le cercle de droite, représentée par le segment mauve, varie en fonction de l'angle et est égal à la valeur de 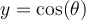 .
.
On remarque que les ordonnées et les abscisses des points du cercle sont toutes comprises entre -1 et 1 inclusivement. Par conséquent,
Pour les autres fonctions trigonométriques, il faut savoir que plus on divise un nombre par une valeur proche de zéro, plus le résultat s'approche de 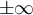 . Ainsi, pour la tangente, puisque
. Ainsi, pour la tangente, puisque
les zéros du cosinus vont créer des asymptotes verticales. En illustrant le tout sur un graphe, on obtient
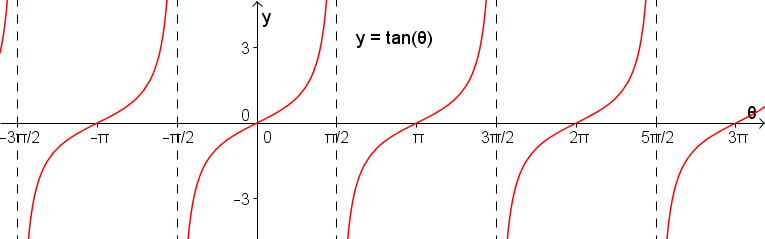
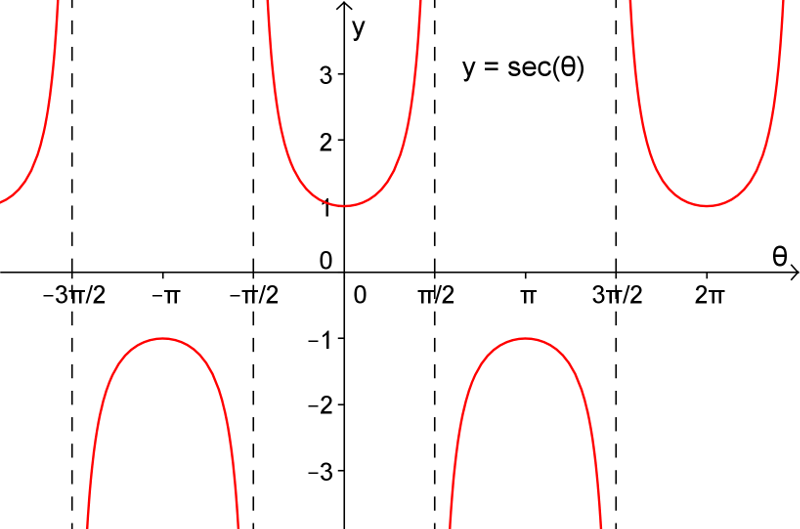
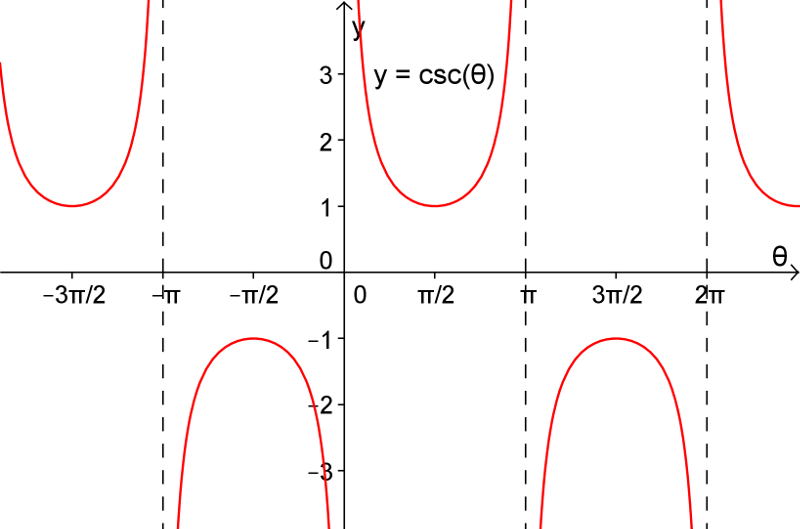
De la même façon, puisque
 |
 |
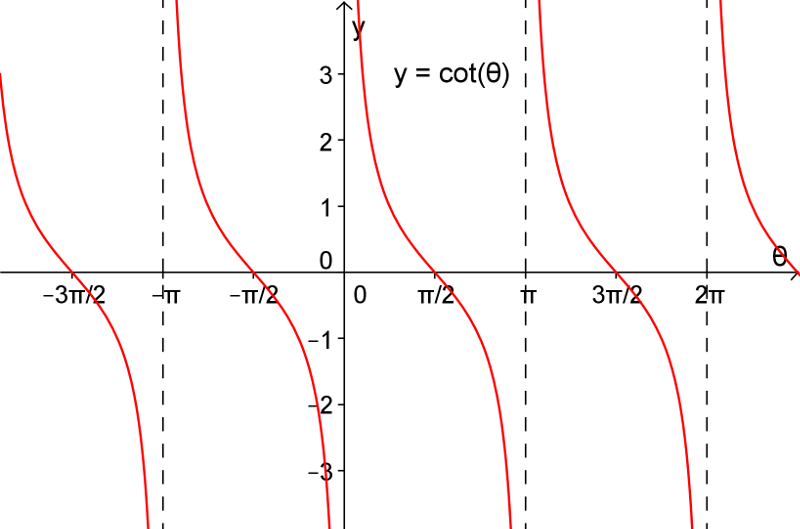 |
| La sécante | La cosécante | La cotangente |
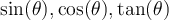
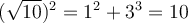
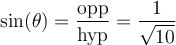
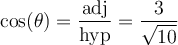
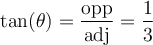
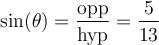
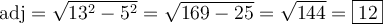
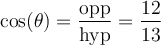
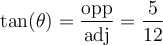
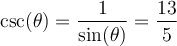
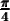
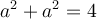
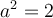
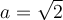
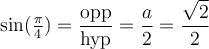
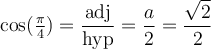
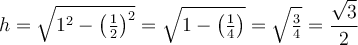
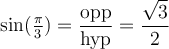
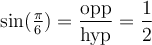
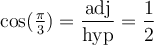
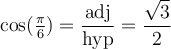
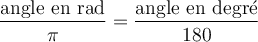
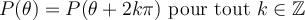
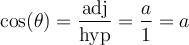
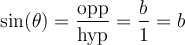
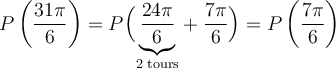

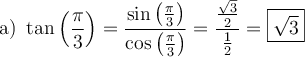
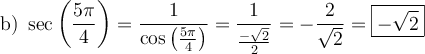

![\begin{array}{ll}\text{c) }\cot\left(\dfrac{-15\pi}{2}\right)&=\cot\Bigl(\underset{\text{3 tours}}{\underbrace{\dfrac{-12\pi}{2}}}+\dfrac{-3\pi}{2}\Bigr)\\[2em]&=\cot\left(\dfrac{-3\pi}{2}\right)=\cot\left(\dfrac{\pi}{2}\right)\\[1em]&=\dfrac{\cos\left(\frac{\pi}{2}\right)}{\sin\left(\frac{\pi}{2}\right)}\\[1em]&=\dfrac{0}{1}\\[1em]&=\boxed{0}\end{array} \begin{array}{ll}\text{c) }\cot\left(\dfrac{-15\pi}{2}\right)&=\cot\Bigl(\underset{\text{3 tours}}{\underbrace{\dfrac{-12\pi}{2}}}+\dfrac{-3\pi}{2}\Bigr)\\[2em]&=\cot\left(\dfrac{-3\pi}{2}\right)=\cot\left(\dfrac{\pi}{2}\right)\\[1em]&=\dfrac{\cos\left(\frac{\pi}{2}\right)}{\sin\left(\frac{\pi}{2}\right)}\\[1em]&=\dfrac{0}{1}\\[1em]&=\boxed{0}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0137c006c88bf87ceeea4b8dc94e8410.png)
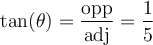
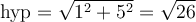
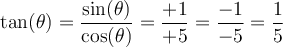
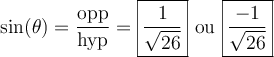
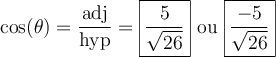
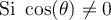
![\begin{array}{lrl}\bullet &\tan(\theta)&=\dfrac{\sin(\theta)}{\cos(\theta)}\\[2em]\bullet&\sec(\theta)&=\dfrac{1}{\cos(\theta)}\end{array} \begin{array}{lrl}\bullet &\tan(\theta)&=\dfrac{\sin(\theta)}{\cos(\theta)}\\[2em]\bullet&\sec(\theta)&=\dfrac{1}{\cos(\theta)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/107791576d776fdaf8a17fa391aafd0d.png)
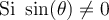
![\begin{array}{lrl}\bullet &\cot(\theta)&=\dfrac{\cos(\theta)}{\sin(\theta)}\\[2em]\bullet &\csc(\theta)&=\dfrac{1}{\sin(\theta)}\end{array} \begin{array}{lrl}\bullet &\cot(\theta)&=\dfrac{\cos(\theta)}{\sin(\theta)}\\[2em]\bullet &\csc(\theta)&=\dfrac{1}{\sin(\theta)}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/73096d79689f33ca6a5e9f9651511b46.png)
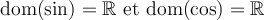
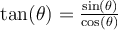
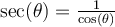
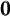
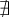
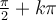
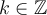
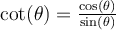
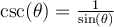
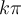
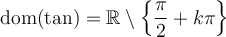
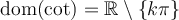
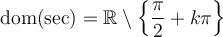
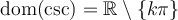
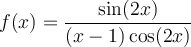
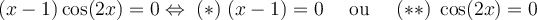
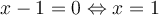
![\begin{array}{ll}\cos(2x)=0&\Leftrightarrow 2x=\dfrac{\pi}{2}+k\pi\text{ où }k\in\mathbb{Z},\\&\text{ car }\cos(\theta)=0\text{ si }\theta=\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\dots\\[1em]&\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}=\dfrac{\pi+2k\pi}{4}=\dfrac{(1+2k)\pi}{4}\end{array} \begin{array}{ll}\cos(2x)=0&\Leftrightarrow 2x=\dfrac{\pi}{2}+k\pi\text{ où }k\in\mathbb{Z},\\&\text{ car }\cos(\theta)=0\text{ si }\theta=\frac{-\pi}{2},\frac{\pi}{2},\frac{3\pi}{2},\dots\\[1em]&\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}=\dfrac{\pi+2k\pi}{4}=\dfrac{(1+2k)\pi}{4}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ac5c0808edae96763fc44d0f5967043d.png)
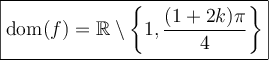

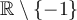
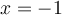
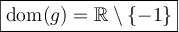
![\text{ima}(\sin)=[-1,1]\quad\text{et}\quad\text{ima}(\cos)=[-1,1] \text{ima}(\sin)=[-1,1]\quad\text{et}\quad\text{ima}(\cos)=[-1,1]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/a1afdea4c87a0c2b88d19531ad0aa8f1.png)