3.3 Fonctions trigonométriques inverses
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 3.3 Fonctions trigonométriques inverses |
| Imprimé par: | Visiteur anonyme |
| Date: | mercredi 8 mai 2024, 23:28 |
Description
- Introduction
- Fonction arcsin
- Fonction arccos
- Fonction arctan
- Autres fonctions trigonométriques inverses
- Résoudre une équation trigonométrique
1. Introduction
Les fonctions trigonométriques inverses sont en quelque sorte les fonctions réciproques des fonctions trigonométriques. Nous avons déjà abordé ce concept, mais rappelons ici la définition d'une fonction réciproque.
L'utilité des fonctions trigonométriques inverses est donc d'isoler l'angle  ou l'argument que l'on donne aux fonctions trigonométriques. Elles sont donc utiles pour résoudre des équations contenant des fonctions trigonométriques. Par exemple,
ou l'argument que l'on donne aux fonctions trigonométriques. Elles sont donc utiles pour résoudre des équations contenant des fonctions trigonométriques. Par exemple,
2. Fonction arcsin
Afin qu'une fonction 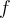 possède une fonction réciproque,
possède une fonction réciproque, 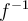 , il faut que
, il faut que 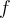 soit une fonction injective, c'est-à-dire qu´à toute valeur
soit une fonction injective, c'est-à-dire qu´à toute valeur 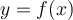 corresponde une seule valeur de
corresponde une seule valeur de  . Or, on constate que la fonction sinus n'est pas une fonction injective et donc ne possède pas de fonction réciproque.
. Or, on constate que la fonction sinus n'est pas une fonction injective et donc ne possède pas de fonction réciproque.
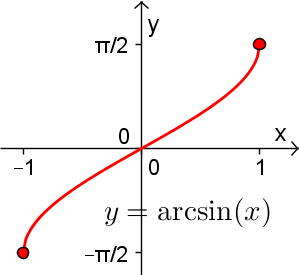
En effet, en observant le graphique de la fonction 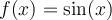 , il existe une droite horizontale qui coupe la courbe de sinus en plusieurs points d'intersection. Cela a comme conséquence que la courbe réciproque de sinus n'est pas une fonction par définition (voir le graphe de droite). Par exemple, il existe plus qu'une image
, il existe une droite horizontale qui coupe la courbe de sinus en plusieurs points d'intersection. Cela a comme conséquence que la courbe réciproque de sinus n'est pas une fonction par définition (voir le graphe de droite). Par exemple, il existe plus qu'une image 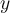 associée à la valeur
associée à la valeur 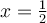 , soit entre autres,
, soit entre autres, 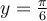 et
et 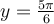 .
.
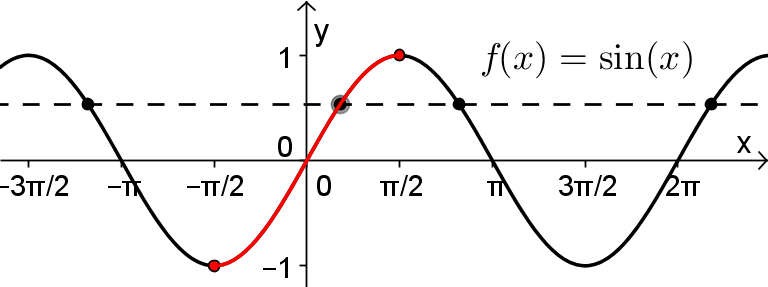

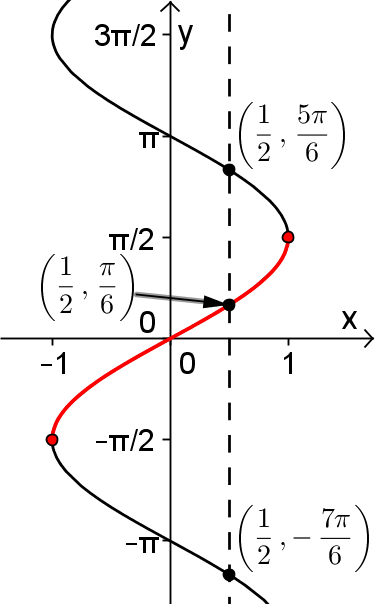
Par conséquent, pour créer la fonction réciproque arcsinus, il faut restreindre le domaine de sinus pour rendre cette fonction injective. Par convention, c'est sur l'intervalle des valeurs ![x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right] x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0d192a1f8b4c6259ea6692cc0e8c2b65.png) qu'est définie notre fonction injective
qu'est définie notre fonction injective 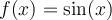 , représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arcsinus de la façon suivante.
, représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arcsinus de la façon suivante.
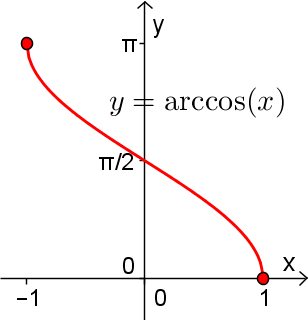
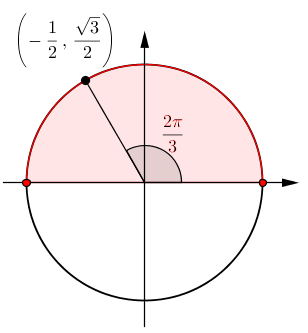
3. Fonction arccos
De la même manière que la fonction arcsinus, la fonction arccosinus est la réciproque d'une fonction injective cosinus définie sur un domaine restreint. En effet, on constate que la fonction 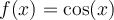 définie sur
définie sur 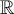 n'est pas injective, et par conséquent sa courbe réciproque n'est pas celle d'une fonction.
n'est pas injective, et par conséquent sa courbe réciproque n'est pas celle d'une fonction.
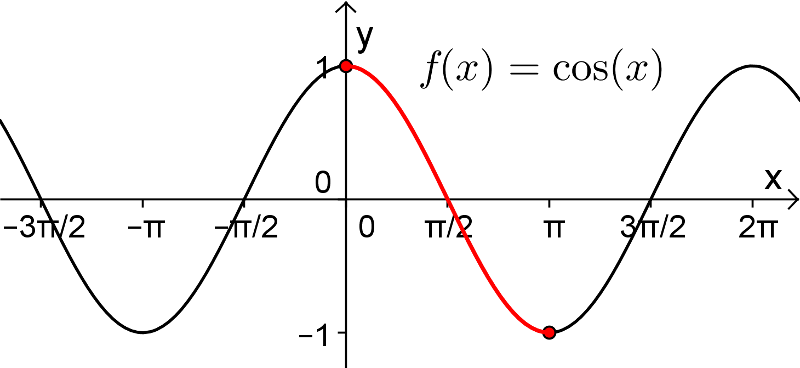

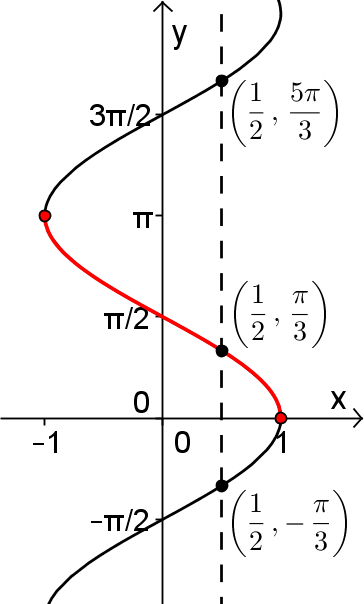
Par convention, c'est sur l'intervalle des valeurs ![x\in\left[0,\pi\right] x\in\left[0,\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e28905bc597d51e5f27a8e9b597f21b6.png) qu'est définie notre fonction injective
qu'est définie notre fonction injective 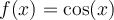 , représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arccosinus de la façon suivante.
, représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arccosinus de la façon suivante.
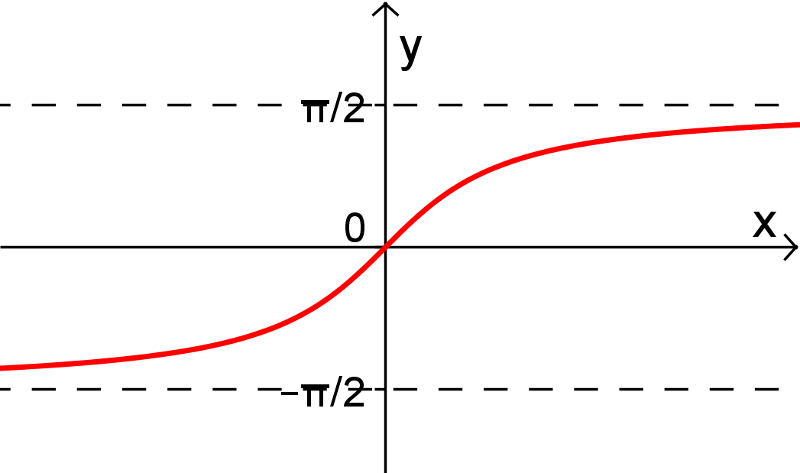
4. Fonction arctan
On peut rendre la fonction tangente injective en restreignant son domaine aux valeurs ![x\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[ x\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6eb648a9b0954c2e5b4b51ea4a961853.png) , comme on peut le voir dans les figures suivantes. La fonction arctangente est donc la réciproque de cette fonction injective et est représentée par la courbe rouge.
, comme on peut le voir dans les figures suivantes. La fonction arctangente est donc la réciproque de cette fonction injective et est représentée par la courbe rouge.
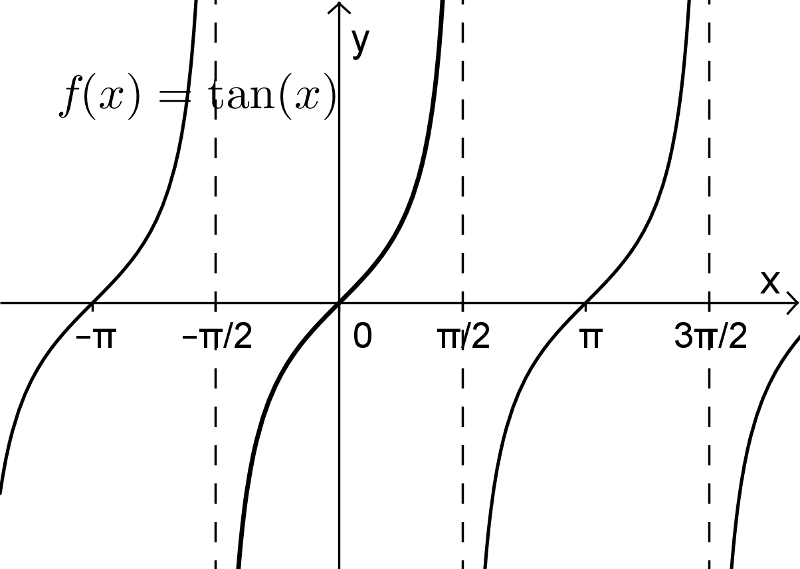

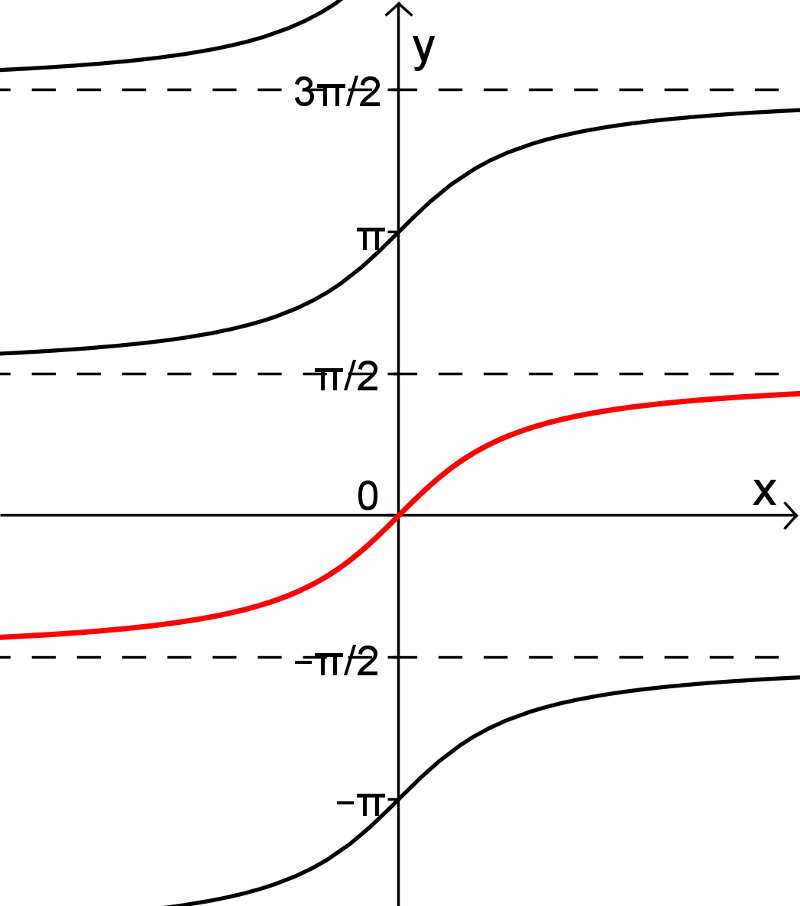
Nous pouvons alors définir la fonction arctangente de la façon suivante.
Exemple : Simplifiez l'expression 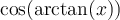 ,
,
En posant l'angle 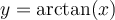 , on cherche donc à simplifier l'expression
, on cherche donc à simplifier l'expression 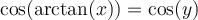 .
.
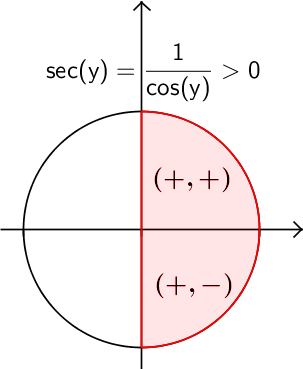
On a par définition que
Sachant que 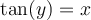 , on peut déterminer la valeur de
, on peut déterminer la valeur de 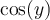 à l'aide de l'identité trigonométrique suivante :
à l'aide de l'identité trigonométrique suivante :
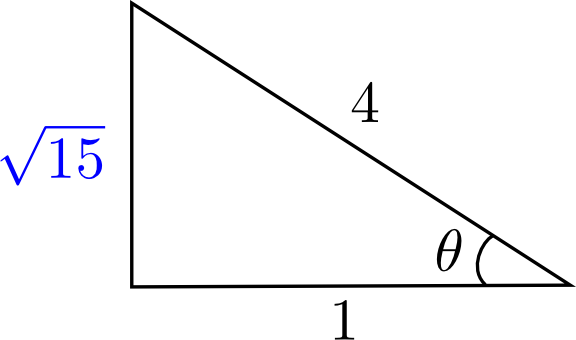
solution2 : À l'aide d'un schéma
Au lieu d'utiliser une identité trigonométrique, nous pourrions construire un triangle rectangle dont les côtés respectent la définition du rapport trigonométrique de tangente : 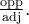
On sait que si 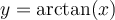 , alors
, alors 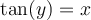 . On a donc
. On a donc
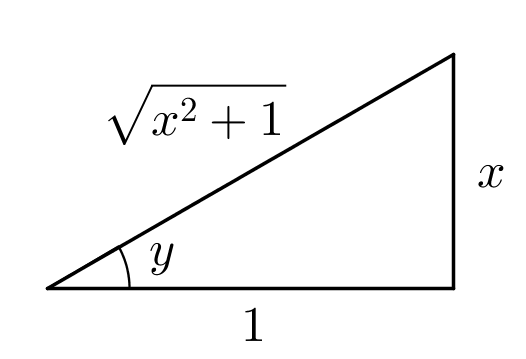
C'est-à-dire le côté opposé est égal à  et le côté adjacent est égal à
et le côté adjacent est égal à 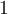 . Par Pythagore, on a que l'hypoténuse doit être égale à
. Par Pythagore, on a que l'hypoténuse doit être égale à 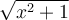 .
.
Ainsi,
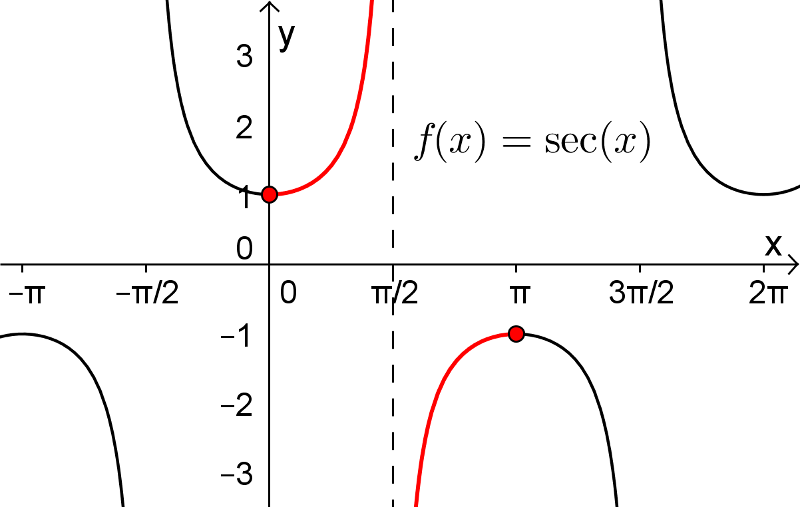
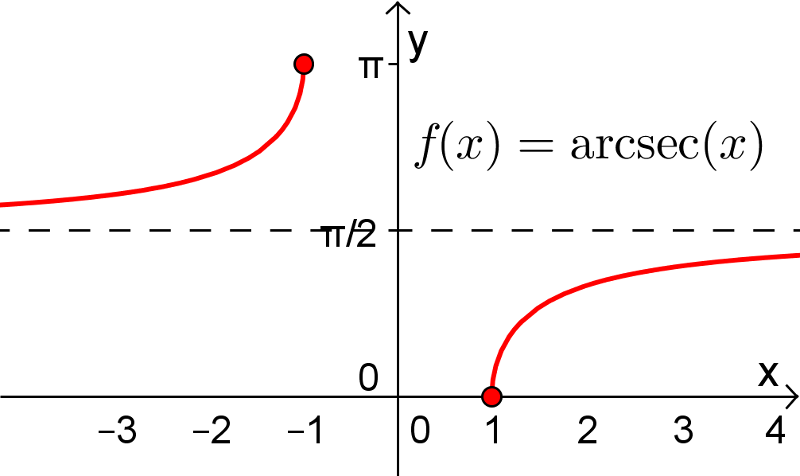
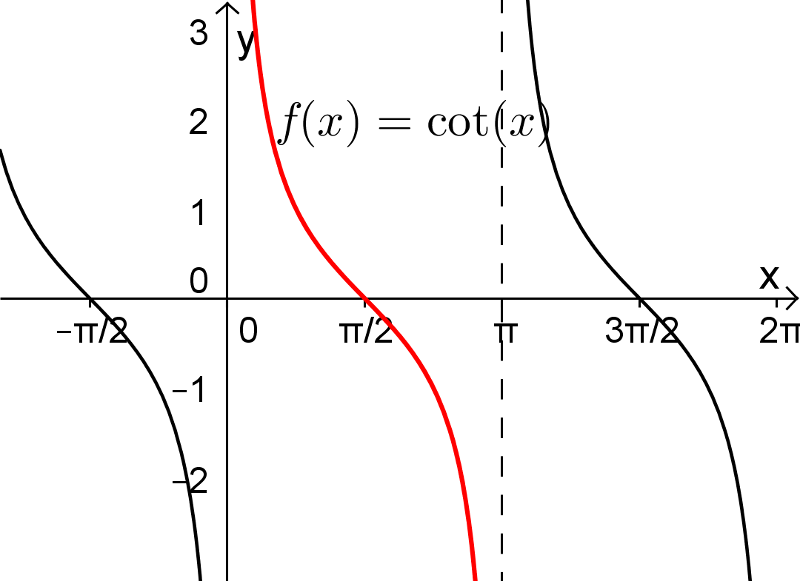
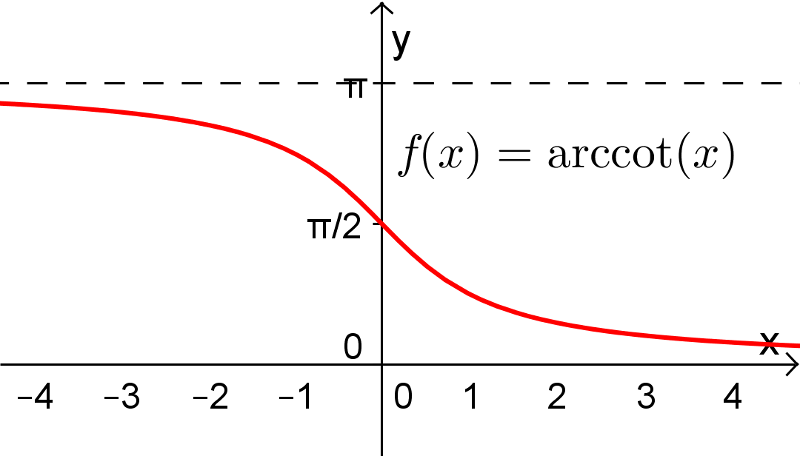
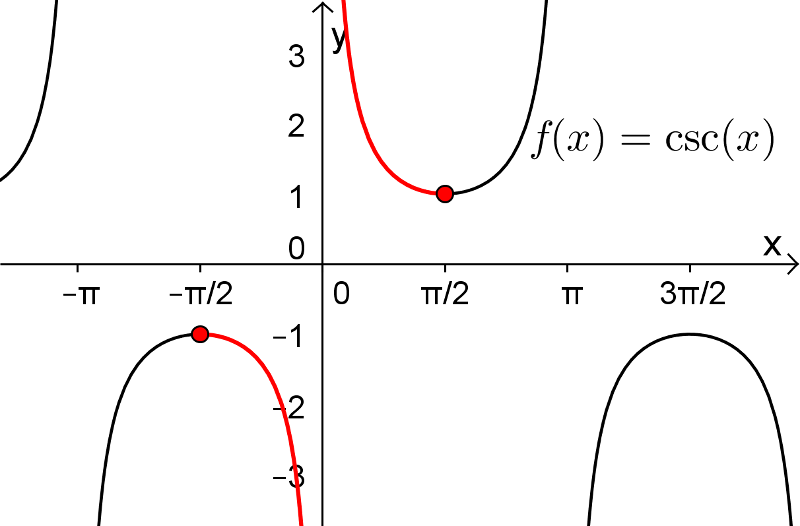
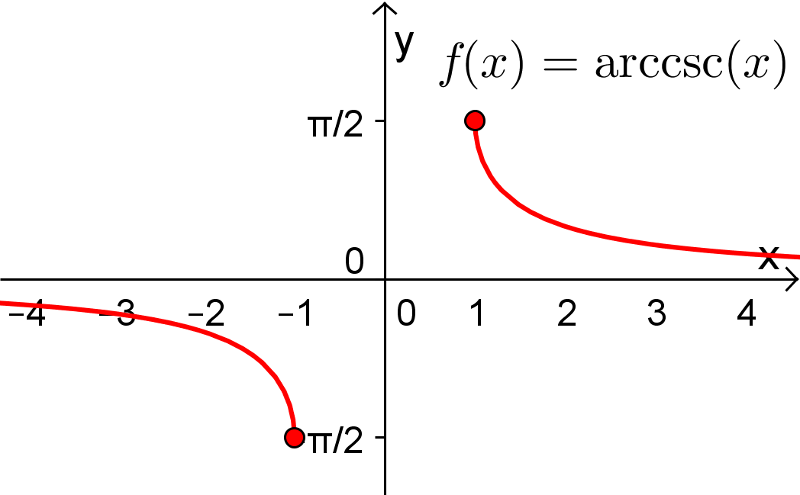
5. Fonctions arcsec, arccot et arccsc
Les fonctions sécante, cotangente et cosécante possèdent également leurs fonctions réciproques sur un intervalle restreint de leur domaine. Pour les fonctions arcsec et arccsc, le choix de l'intervalle restreint pour  ne fait pas l'unanimité chez plusieurs mathématiciens en raison du signe de la dérivée de ces fonctions. Tout cela vous sera expliqué dans votre cours Calcul différentiel. Voici les définitions de ces trois dernières fonctions réciproques.
ne fait pas l'unanimité chez plusieurs mathématiciens en raison du signe de la dérivée de ces fonctions. Tout cela vous sera expliqué dans votre cours Calcul différentiel. Voici les définitions de ces trois dernières fonctions réciproques.
6. Résoudre une équation trigonométrique
Résoudre une équation contenant des fonctions trigonométriques signifie trouver l'angle qui vérifie cette équation dans les restrictions données. Nous avons fait quelques exemples de ce type de problème dans les sections précédentes. Nous allons voir dans la présente section d'autres situations où il faut déterminer la valeur d'un angle.
Voici quelques étapes qui nous aideront dans notre résolution.
- Déterminer le domaine de l'équation et les restrictions.
-
Transformer l'équation en une ou plusieurs équations équivalentes de la forme
Vous pouvez utiliser les définitions des rapports trigonométriques, ainsi que les identités afin de transformer votre équation.
- Chercher sur le cercle trigonométrique les angles
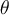 correspondant aux valeurs de sinus ou cosinus et respectant le domaine de l'équation.
correspondant aux valeurs de sinus ou cosinus et respectant le domaine de l'équation.
Exemples : Résoudre les équations suivantes.
Solution
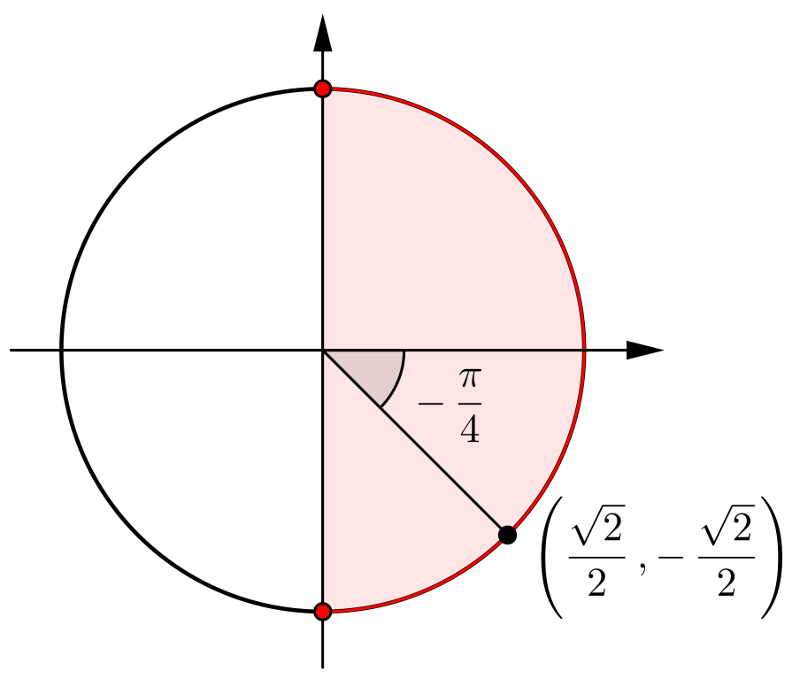
- Le domaine de cette équation est
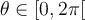 et il n'y a aucune restriction pour sinus.
et il n'y a aucune restriction pour sinus. 
Isolons la fonction sinus :
- Sur le cercle trigonométrique, on a
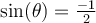 si
si 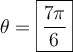 et
et 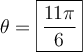 . Ces deux valeurs font partie du domaine.
. Ces deux valeurs font partie du domaine.
Solution On transforme tout d'abord le membre de droite pour obtenir des sinus et cosinus.
- Sur l'intervalle
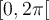 , il y a deux restrictions :
, il y a deux restrictions : 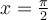 et
et 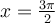 , car, pour ces deux valeurs, le dénominateur
, car, pour ces deux valeurs, le dénominateur 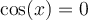 .
. -
Simplifions cette équation.
Ainsi, chacun des facteurs de cette dernière équation peut être égal à 0. C'est-à-dire
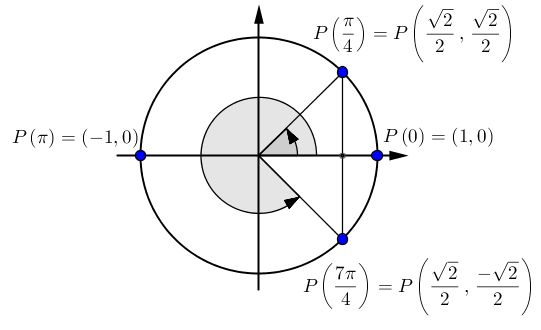
Pour l'équation (1), les valeurs de l'angle
 pour lesquelles
pour lesquelles 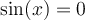 sont
sont  et
et 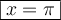 .
.Pour l'équation (2), on trouve sur le cercle trigonométrique les valeurs de l'angle
 pour lesquelles
pour lesquelles 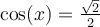 . Soit
. Soit
Ces quatre solutions font partie du domaine de l'équation et respectent les restrictions.
Exemple : Déterminer le domaine de la fonction 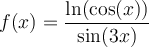 .
.
Solution Le domaine de cette fonction dépend des restrictions suivantes :
-
La fonction logarithmique ln est définie pour des arguments strictement positifs (> 0). Par conséquent, il faut que son argument
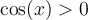 .
.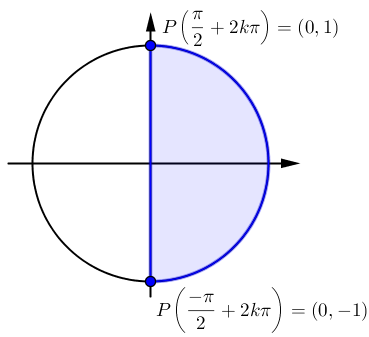
On trouve sur le cercle trigonométrique que les valeurs de l'angle
 pour lesquelles la valeur de cosinus est strictement positive sont
pour lesquelles la valeur de cosinus est strictement positive sont ![\left]\frac{-\pi}{2},\frac{\pi}{2}\right[ \left]\frac{-\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7a3a937ab84dac291b827974ef47af89.png) .
.Par contre, on sait également qu'en faisant des tours complets sur le cercle, il existe d'autres valeurs
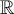 pour lesquelles cosinus est
pour lesquelles cosinus est 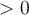 . Étant donné que
. Étant donné que -
La deuxième restriction est que le dénominateur doit être non nul. Par conséquent, il faut que
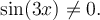
On a que
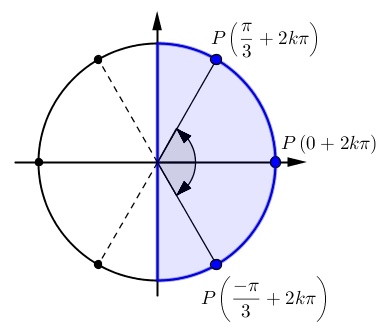
En situant les valeurs où
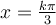 sur le cercle trigonométrique, on constate que seulement trois points font partie de l'intervalle de la restriction précédente :
sur le cercle trigonométrique, on constate que seulement trois points font partie de l'intervalle de la restriction précédente :Il faut donc exclure du domaine de
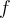 ces valeurs de
ces valeurs de  pour lesquelles
pour lesquelles 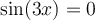 et qui se trouvent dans l'intervalle
et qui se trouvent dans l'intervalle ![x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[. x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[.](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/00bcc3627b91eb0e653741d68125be3d.png)
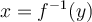
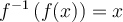
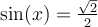
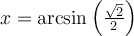
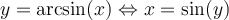
![y\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right] y\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/4a2da7ec8101d96f3f6dc9128b84a387.png)
![\text{dom}(\arcsin)=[-1,1] \text{dom}(\arcsin)=[-1,1]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7521eda7044f5661480e3f2eb1f81b53.png)
![\text{ima}(\arcsin)=\left[-\frac{\pi}{2},\frac{\pi}{2}\right] \text{ima}(\arcsin)=\left[-\frac{\pi}{2},\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ffb3373e70ff9d2373fb614fdca9ac74.png)
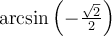

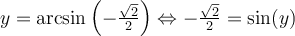
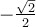
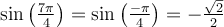
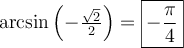
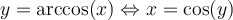
![y\in\left[0,\pi\right] y\in\left[0,\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0558feb0113ff6831af2332059a18985.png)
![\text{dom}(\arccos)=[-1,1] \text{dom}(\arccos)=[-1,1]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/76dcfaae0d48271dfb85d15877de31b4.png)
![\text{ima}(\arccos)=\left[0,\pi\right] \text{ima}(\arccos)=\left[0,\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/16a45cf9c303248688c1d3428f7a806a.png)
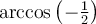
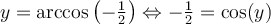
![y\in [0,\pi] y\in [0,\pi]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cf1f64a90a341c31ef34ddfd24c671ba.png)
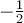
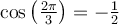
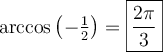
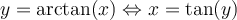
![y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[ y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d3cb5a455333a1e5c4b61b0b6f16df51.png)
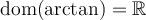
![\text{ima}(\arctan)=\left]-\frac{\pi}{2},\frac{\pi}{2}\right[ \text{ima}(\arctan)=\left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/4a86e3c2bd8a8ef2553a806baf6c9379.png)
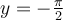
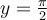
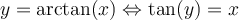
![y\in \left]-\frac{\pi}{2},\frac{\pi}{2}\right[ y\in \left]-\frac{\pi}{2},\frac{\pi}{2}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ddb9017d40ae21628b43743eca930757.png)
![\begin{array}{rll}\tan^2(y)+1&=\sec^2(y)&\\x^2+1&=\sec^2(y)&\small\text{; car }\tan(y)=x\\\sqrt{x^2+1}&=+\sec(y)&\small\text{ puisque }y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[,\\[-0.5em]&&\small\text{ alors }\sec{y} > 0\\\sqrt{x^2+1}&=\dfrac{1}{\cos(y)}&\\\cos(y)&=\dfrac{1}{\sqrt{x^2+1}}&\end{array} \begin{array}{rll}\tan^2(y)+1&=\sec^2(y)&\\x^2+1&=\sec^2(y)&\small\text{; car }\tan(y)=x\\\sqrt{x^2+1}&=+\sec(y)&\small\text{ puisque }y\in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[,\\[-0.5em]&&\small\text{ alors }\sec{y} > 0\\\sqrt{x^2+1}&=\dfrac{1}{\cos(y)}&\\\cos(y)&=\dfrac{1}{\sqrt{x^2+1}}&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/4eee0b9ee13ff14593f3a1442304fa17.png)
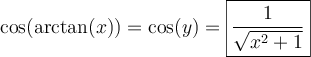
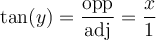
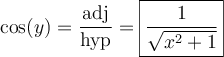
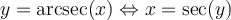
![y\in\left[0,\frac{\pi}{2}\right[\cup\left]\frac{\pi}{2},\pi\right] y\in\left[0,\frac{\pi}{2}\right[\cup\left]\frac{\pi}{2},\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c7b1a86e07a554cbcd2afa6c5641e6ad.png)
![\text{dom}(\text{arcsec})=]-\infty,-1]\cup[1,\infty[ \text{dom}(\text{arcsec})=]-\infty,-1]\cup[1,\infty[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3c78b49eb2f0926e4a7d3f5ff72c79d7.png)
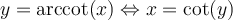
![y\in\left]0,\pi\right[ y\in\left]0,\pi\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/81a8984d324c8954afbb0dd54d7216cd.png)
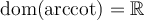
![y\in\left[-\frac{\pi}{2},0\right[\cup\left]0,\frac{\pi}{2}\right] y\in\left[-\frac{\pi}{2},0\right[\cup\left]0,\frac{\pi}{2}\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cb21661f30a4dae2fe502249dacd3715.png)
![\text{dom}(\text{arccsc})=\left]-\infty,-1]\cup [1,\infty\right[ \text{dom}(\text{arccsc})=\left]-\infty,-1]\cup [1,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c472018bddbce3a41f4f1804bec64b01.png)
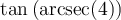
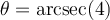
![\theta\in\left[0,\pi\right]\setminus\left\lbrace\frac{\pi}{2}\right\rbrace \theta\in\left[0,\pi\right]\setminus\left\lbrace\frac{\pi}{2}\right\rbrace](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8625cfdf1b563518029ab545d1a0d25c.png)
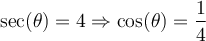
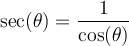
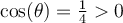
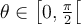

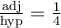
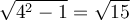
![\begin{array}{rll}\tan\left(\text{arcsec}(4)\right)&=\tan(\theta)&\small\text{; car }\theta=\text{arcsec}(4)\\&=\dfrac{\sqrt{15}}{1}&\small\text{; car }\tan(\theta)=\frac{\text{opp}}{\text{adj}}\\[1em]&=\sqrt{15}&\end{array} \begin{array}{rll}\tan\left(\text{arcsec}(4)\right)&=\tan(\theta)&\small\text{; car }\theta=\text{arcsec}(4)\\&=\dfrac{\sqrt{15}}{1}&\small\text{; car }\tan(\theta)=\frac{\text{opp}}{\text{adj}}\\[1em]&=\sqrt{15}&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f80624bf3e856c7eb7ede980a00d7ba4.png)
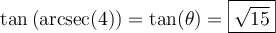
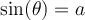
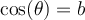
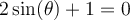
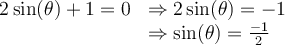
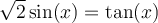
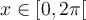
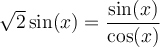
![\begin{array}{rll}\sqrt{2}\sin(x)&=\dfrac{\sin(x)}{\cos(x)}&\\[1em]\sqrt{2}\sin(x)\cos(x)&=\sin(x)&\small\text{; on a multiplié chaque}\\&&\small\text{ membre par }\cos(x)\\\sqrt{2}\sin(x)\cos(x)-\sin(x)&=0&\\[1em]\underset{(1)}{\underbrace{\sin(x)}}\underset{(2)}{\underbrace{\left(\sqrt{2}\cos(x)-1\right)}}&=0&\small\text{; on a factorisé}\end{array} \begin{array}{rll}\sqrt{2}\sin(x)&=\dfrac{\sin(x)}{\cos(x)}&\\[1em]\sqrt{2}\sin(x)\cos(x)&=\sin(x)&\small\text{; on a multiplié chaque}\\&&\small\text{ membre par }\cos(x)\\\sqrt{2}\sin(x)\cos(x)-\sin(x)&=0&\\[1em]\underset{(1)}{\underbrace{\sin(x)}}\underset{(2)}{\underbrace{\left(\sqrt{2}\cos(x)-1\right)}}&=0&\small\text{; on a factorisé}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2fda081a813fbf3567e6baa15955e4af.png)
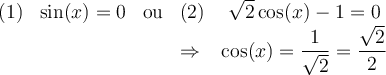
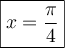
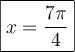
![\begin{array}{rl}P\left(\frac{-\pi}{2}\right)&=P\left(\frac{-\pi}{2}+2k\pi\right)\\[1em]\text{et }P\left(\frac{\pi}{2}\right)&=P\left(\frac{\pi}{2}+2k\pi\right)\end{array} \begin{array}{rl}P\left(\frac{-\pi}{2}\right)&=P\left(\frac{-\pi}{2}+2k\pi\right)\\[1em]\text{et }P\left(\frac{\pi}{2}\right)&=P\left(\frac{\pi}{2}+2k\pi\right)\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9afc16ee56da2ba8e3eac9987fc6cd7b.png)
![x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[ x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/01a92d51c8a6652c32afb757807ce9aa.png)
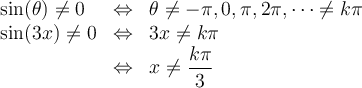
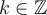
![\begin{array}{rl}P\left(\frac{-\pi}{3}\right)&=P\left(\frac{-\pi}{3}+2k\pi\right)\\[1em]P(0)&=P(2k\pi)\\[1em]P\left(\frac{\pi}{3}\right)&=P\left(\frac{\pi}{3}+2k\pi\right)\end{array} \begin{array}{rl}P\left(\frac{-\pi}{3}\right)&=P\left(\frac{-\pi}{3}+2k\pi\right)\\[1em]P(0)&=P(2k\pi)\\[1em]P\left(\frac{\pi}{3}\right)&=P\left(\frac{\pi}{3}+2k\pi\right)\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/37f05ce0b84e4a49ec34bbfe544ecb2c.png)
![\text{dom}\left(\frac{\ln(\cos(x))}{\sin(3x)}\right)=x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[\setminus\left\lbrace\frac{-\pi}{3}+2k\pi, 2k\pi,\frac{\pi}{3}+2k\pi\right\rbrace \text{dom}\left(\frac{\ln(\cos(x))}{\sin(3x)}\right)=x\in\left]\frac{-\pi}{2}+2k\pi,\frac{\pi}{2}+2k\pi\right[\setminus\left\lbrace\frac{-\pi}{3}+2k\pi, 2k\pi,\frac{\pi}{3}+2k\pi\right\rbrace](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c04a95e3a526250c513de5fa8f0c0ece.png)