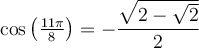3.2 Les identités trigonométriques
- Introduction
- Identités de base
- Formules trigonométriques utiles
- Formules d'addition d'angles
- Démonstration d'une identité
4. Formules d'addition d'angles
Les formules suivantes permettent de calculer le sinus et le cosinus d'une somme ou d'une différence d'angles.
Cliquez sur le lien suivant pour voir une démonstration de la formule d'addition d'angle de la fonction sinus. Les autres formules se démontrent d'une façon similaire.
Exemple : On peut calculer la valeur de 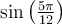 avec la formule 1 d'addition d'angles et les valeurs du sinus et cosinus d'angles remarquables. En effet,
avec la formule 1 d'addition d'angles et les valeurs du sinus et cosinus d'angles remarquables. En effet,
Par conséquent, on obtient :
À partir des formules d'addition d'angles, nous pouvons également créer deux nouvelles identités, celles du double des angles.
En voici les démonstrations :
Finalement, la formule 6 nous permet de créer ces deux dernières formules liées aux carrés des fonctions sinus et cosinus qui serviront en calcul intégral.
En voici les démonstrations :
-
Sachant que
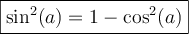 , on peut la remplacer dans la formule 6,
, on peut la remplacer dans la formule 6, 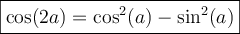 , pour obtenir
, pour obtenir -
Sachant que
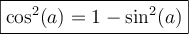 , on peut la remplacer dans la formule 6,
, on peut la remplacer dans la formule 6, 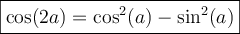 , pour obtenir
, pour obtenir
Exemple : On peut calculer la valeur de 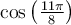 avec la formule 7 et la valeur du cosinus d'angles remarquables. En effet, en posant
avec la formule 7 et la valeur du cosinus d'angles remarquables. En effet, en posant
on obtient :
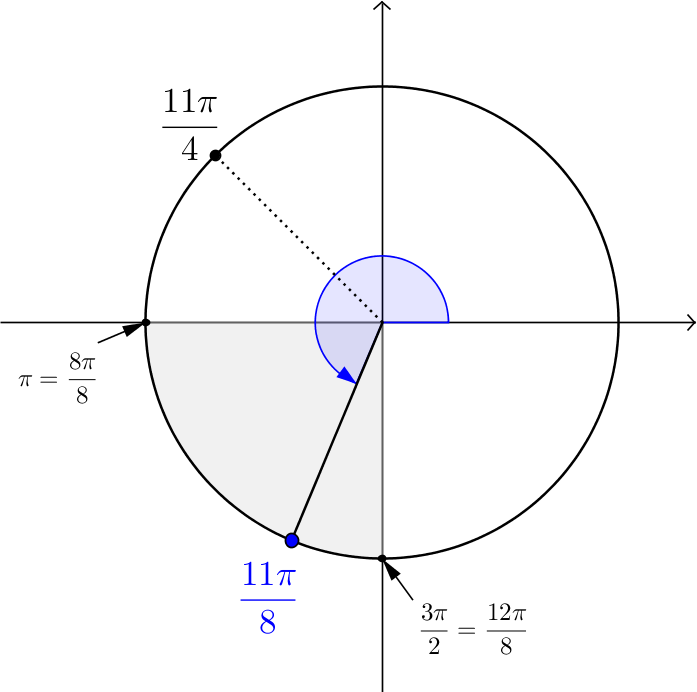
Finalement, on détermine le signe de 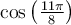 en plaçant un point sur le cercle trigonométrique situé à un angle de
en plaçant un point sur le cercle trigonométrique situé à un angle de 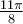 , soit dans le troisième quadrant. Par conséquent, on aura une valeur négative.
, soit dans le troisième quadrant. Par conséquent, on aura une valeur négative.
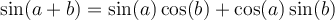
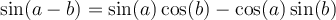
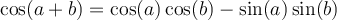
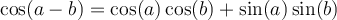
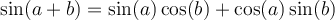
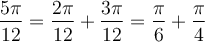
![\begin{array}{ll}\sin\left(\frac{5\pi}{12}\right)&=\sin\left(\frac{\pi}{6}+\frac{\pi}{4}\right)\\[1em]&=\sin\left(\frac{\pi}{6}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{6}\right)\sin\left(\frac{\pi}{4}\right)\\[1em]&=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\[1em]&=\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}\\[1em]&=\boxed{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\end{array} \begin{array}{ll}\sin\left(\frac{5\pi}{12}\right)&=\sin\left(\frac{\pi}{6}+\frac{\pi}{4}\right)\\[1em]&=\sin\left(\frac{\pi}{6}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{6}\right)\sin\left(\frac{\pi}{4}\right)\\[1em]&=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\[1em]&=\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}\\[1em]&=\boxed{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f79e9717b8d7cdbc2101706902fb89bf.png)
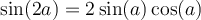
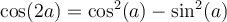
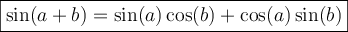
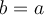
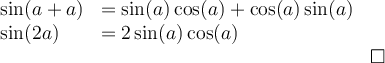
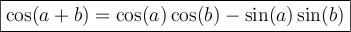
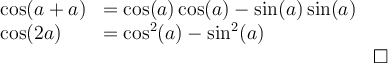
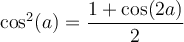
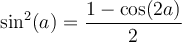
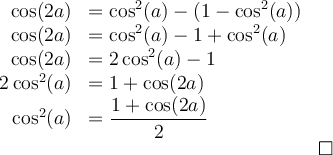
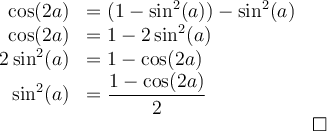
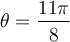
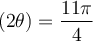
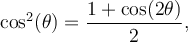
![\begin{array}{ll}\cos\left(\frac{11\pi}{8}\right)&=\pm\sqrt{\dfrac{1+\cos\left(\frac{11\pi}{4}\right)}{2}}\\[1em]&=\pm\sqrt{\dfrac{1-\frac{\sqrt{2}}{2}}{2}} \\[1em]&=\pm\sqrt{\dfrac{2-\sqrt{2}}{4}}\\[1em]&=\pm\dfrac{\sqrt{2-\sqrt{2}}}{2}\end{array} \begin{array}{ll}\cos\left(\frac{11\pi}{8}\right)&=\pm\sqrt{\dfrac{1+\cos\left(\frac{11\pi}{4}\right)}{2}}\\[1em]&=\pm\sqrt{\dfrac{1-\frac{\sqrt{2}}{2}}{2}} \\[1em]&=\pm\sqrt{\dfrac{2-\sqrt{2}}{4}}\\[1em]&=\pm\dfrac{\sqrt{2-\sqrt{2}}}{2}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ad33462fe4f9e7b66e8972ec58031c9e.png)