3.2 Les identités trigonométriques
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 3.2 Les identités trigonométriques |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 07:47 |
Description
- Introduction
- Identités de base
- Formules trigonométriques utiles
- Formules d'addition d'angles
- Démonstration d'une identité
1. Introduction
Dans cette section, nous allons démontrer et illustrer les différentes formules de trigonométrie qui sont utiles au cours du cursus collégial et qui servent à simplifier des expressions trigonométriques.
Par définition, une identité trigonométrique est une égalité permettant de transformer une expression trigonométrique en une expression équivalente, mais plus simple.
Voici une liste qui regroupe les identités trigonométriques les plus courantes.
2. Identités de base
Soit le triangle
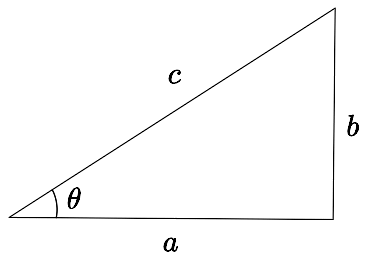
L'identité à la base de toutes les autres s'appelle le théorème de Pythagore.
En divisant par 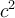 de chaque côté, on obtient
de chaque côté, on obtient
Par conséquent, en utilisant les définitions des fonctions trigonométriques, on obtient
Afin de trouver les deux autres identités de base, il suffit de diviser l'équation ci-dessus par 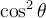 ou par
ou par 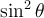 .
.
En effet,
3. Formules trigonométriques utiles
Les formules trigonométriques proviennent des propriétés des angles associés suivants :
- Les angles opposés
- Les angles complémentaires et anticomplémentaires
- Les angles supplémentaires et antisupplémentaires
Angles opposés
Deux angles sont opposés si et seulement si leur somme est égale à 0. Les angles 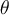 et
et 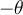 sont opposés et à l'aide du cercle trigonométrique ci-contre, on peut en déduire ces formules :
sont opposés et à l'aide du cercle trigonométrique ci-contre, on peut en déduire ces formules :
Exemple : 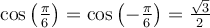 , car les angles
, car les angles 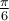 et
et 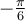 sont deux angles opposés,
sont deux angles opposés, 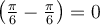 .
.
On a vu précédemment que la valeur du cosinus des angles 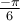 et
et 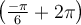 est la même. On peut en déduire également l'égalité suivante :
est la même. On peut en déduire également l'égalité suivante :
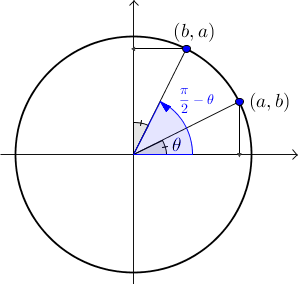
Angles complémentaires et anticomplémentaires
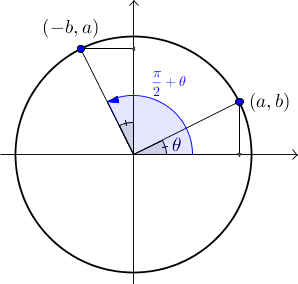
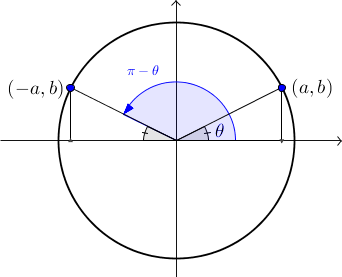
Deux angles sont complémentaires si et seulement si leur somme est égale à 90°, tandis que deux angles sont anticomplémentaires si et seulement si la valeur absolue de leur différence est égale à 90°. Les angles 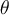 et
et 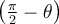 sont complémentaires et les angles
sont complémentaires et les angles 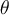 et
et 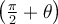 sont anticomplémentaires. À l'aide des figures, on peut en déduire les formules suivantes :
sont anticomplémentaires. À l'aide des figures, on peut en déduire les formules suivantes :
Angles supplémentaires et antisupplémentaires
Deux angles sont supplémentaires si et seulement si leur somme est égale à 180°, tandis que deux angles sont antisupplémentaires si et seulement si la valeur absolue de leur différence est égale à 180°. Les angles 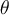 et
et 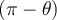 sont supplémentaires et les angles
sont supplémentaires et les angles 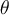 et
et 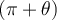 sont antisupplémentaires.
sont antisupplémentaires.
Exemples :
a) 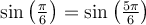 , car les angles
, car les angles 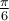 et
et 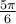 sont deux angles supplémentaires,
sont deux angles supplémentaires, 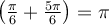 .
.
b) 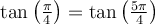 , car les angles
, car les angles 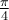 et
et 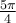 sont deux angles antisupplémentaires,
sont deux angles antisupplémentaires, 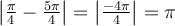 .
.
Exercices formatifs WeBWorK
 Formules trigonométriques utiles
Formules trigonométriques utiles
4. Formules d'addition d'angles
Les formules suivantes permettent de calculer le sinus et le cosinus d'une somme ou d'une différence d'angles.
Cliquez sur le lien suivant pour voir une démonstration de la formule d'addition d'angle de la fonction sinus. Les autres formules se démontrent d'une façon similaire.
Exemple : On peut calculer la valeur de 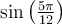 avec la formule 1 d'addition d'angles et les valeurs du sinus et cosinus d'angles remarquables. En effet,
avec la formule 1 d'addition d'angles et les valeurs du sinus et cosinus d'angles remarquables. En effet,
Par conséquent, on obtient :
À partir des formules d'addition d'angles, nous pouvons également créer deux nouvelles identités, celles du double des angles.
En voici les démonstrations :
Finalement, la formule 6 nous permet de créer ces deux dernières formules liées aux carrés des fonctions sinus et cosinus qui serviront en calcul intégral.
En voici les démonstrations :
-
Sachant que
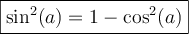 , on peut la remplacer dans la formule 6,
, on peut la remplacer dans la formule 6, 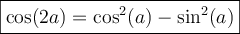 , pour obtenir
, pour obtenir -
Sachant que
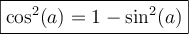 , on peut la remplacer dans la formule 6,
, on peut la remplacer dans la formule 6, 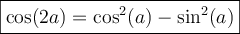 , pour obtenir
, pour obtenir
Exemple : On peut calculer la valeur de 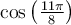 avec la formule 7 et la valeur du cosinus d'angles remarquables. En effet, en posant
avec la formule 7 et la valeur du cosinus d'angles remarquables. En effet, en posant
on obtient :
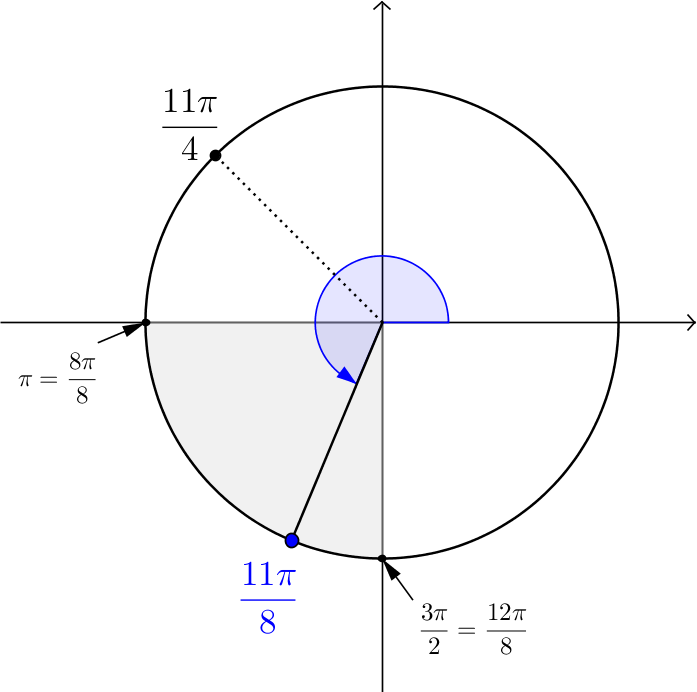
Finalement, on détermine le signe de 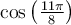 en plaçant un point sur le cercle trigonométrique situé à un angle de
en plaçant un point sur le cercle trigonométrique situé à un angle de 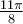 , soit dans le troisième quadrant. Par conséquent, on aura une valeur négative.
, soit dans le troisième quadrant. Par conséquent, on aura une valeur négative.
Exercices formatifs WeBWorK
 Formules d'addition d'angles
Formules d'addition d'angles
5. Démonstration d'une identité
On peut démontrer des identités plus complexes à l'aide des définitions des fonctions trigonométriques et des identités et formules démontrées précédemment. Il n'existe pas de démarche infaillible pour démontrer une identité, il faut souvent utiliser son intuition et son imagination, en se laissant guider par les opérations présentées et par les identités connues. En voici quelques exemples :
Exemples : Démontrons les identités suivantes.
Il faut tout d'abord exprimer tous les membres de cette équation en terme de sinus et cosinus. Nous allons développer le membre de droite de cette égalité, c'est-à-dire le transformer pour obtenir le membre de gauche.
L'identité est vérifiée.
Nous allons développer le membre de gauche de cette égalité pour obtenir celui de droite, car il est plus complexe, et par le fait même, peut se transformer plus facilement.
L'identité est vérifiée.
Nous allons développer le membre de gauche de cette égalité pour obtenir celui de droite, pour les mêmes raisons qu'à l'exemple précédent.
Tout d'abord, observons les identités connues qui pourraient nous être utiles, car elles contiennent des expressions qui se trouvent également dans l'identité à démontrer :
Nous allons utiliser les identités (1) et (3) pour développer notre membre de gauche.
L'identité est vérifiée.
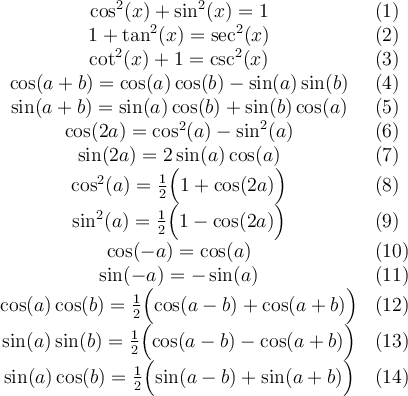
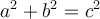
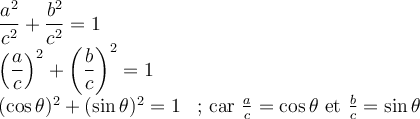
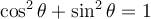
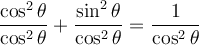
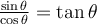
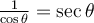
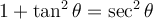
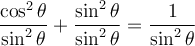
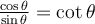
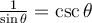
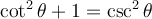
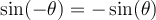
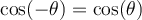

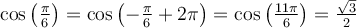
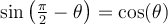
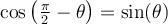
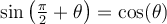
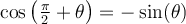
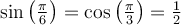
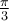
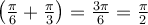
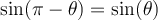
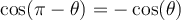
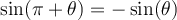
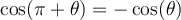

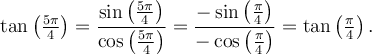
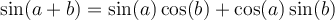
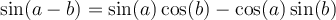
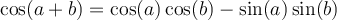
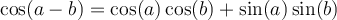
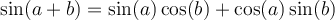
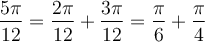
![\begin{array}{ll}\sin\left(\frac{5\pi}{12}\right)&=\sin\left(\frac{\pi}{6}+\frac{\pi}{4}\right)\\[1em]&=\sin\left(\frac{\pi}{6}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{6}\right)\sin\left(\frac{\pi}{4}\right)\\[1em]&=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\[1em]&=\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}\\[1em]&=\boxed{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\end{array} \begin{array}{ll}\sin\left(\frac{5\pi}{12}\right)&=\sin\left(\frac{\pi}{6}+\frac{\pi}{4}\right)\\[1em]&=\sin\left(\frac{\pi}{6}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{6}\right)\sin\left(\frac{\pi}{4}\right)\\[1em]&=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\\[1em]&=\dfrac{\sqrt{6}}{4}+\dfrac{\sqrt{2}}{4}\\[1em]&=\boxed{\dfrac{\sqrt{6}+\sqrt{2}}{4}}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/f79e9717b8d7cdbc2101706902fb89bf.png)
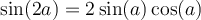
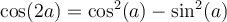
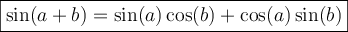
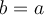
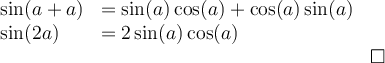
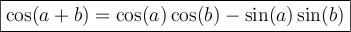
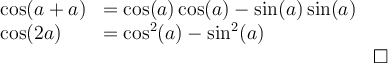
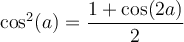
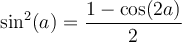
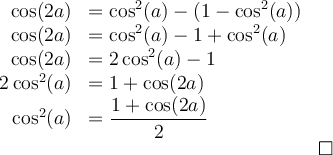
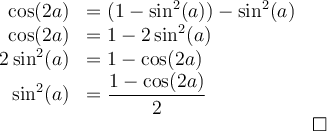
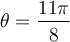
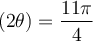
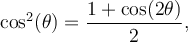
![\begin{array}{ll}\cos\left(\frac{11\pi}{8}\right)&=\pm\sqrt{\dfrac{1+\cos\left(\frac{11\pi}{4}\right)}{2}}\\[1em]&=\pm\sqrt{\dfrac{1-\frac{\sqrt{2}}{2}}{2}} \\[1em]&=\pm\sqrt{\dfrac{2-\sqrt{2}}{4}}\\[1em]&=\pm\dfrac{\sqrt{2-\sqrt{2}}}{2}\end{array} \begin{array}{ll}\cos\left(\frac{11\pi}{8}\right)&=\pm\sqrt{\dfrac{1+\cos\left(\frac{11\pi}{4}\right)}{2}}\\[1em]&=\pm\sqrt{\dfrac{1-\frac{\sqrt{2}}{2}}{2}} \\[1em]&=\pm\sqrt{\dfrac{2-\sqrt{2}}{4}}\\[1em]&=\pm\dfrac{\sqrt{2-\sqrt{2}}}{2}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ad33462fe4f9e7b66e8972ec58031c9e.png)
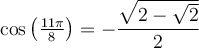
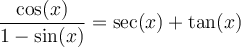
![\begin{array}{ll}\sec(x)+\tan(x)&\\[0.7em]=\dfrac{1}{\cos(x)}+\dfrac{\sin(x)}{\cos(x)}&\small{\text{; définition de }\tan(x)\text{ et }\sec(x)}\\[1em]=\dfrac{1+\sin(x)}{\cos(x)}&\\[1em]=\dfrac{(1+\sin(x))}{\cos(x)}\cdot\dfrac{(1-\sin(x))}{(1-\sin(x))}&\small\text{; multiplication par le conjugué du numérateur}\\[1em]=\dfrac{1-\sin^2(x)}{\cos(x)(1-\sin(x))}&\small ;\;(1+\sin(x))(1-\sin(x))=1-\sin^2(x)\\[1em]=\dfrac{\cos^2(x)}{\cos(x)(1-\sin(x))}&\small{\text{; identité }\cos^2(x)=1-\sin^2(x)}\\[1em]=\dfrac{\cos(x)}{1-\sin(x)}&\small{\text{; simplication par }\cos(x)}\\&\square\end{array} \begin{array}{ll}\sec(x)+\tan(x)&\\[0.7em]=\dfrac{1}{\cos(x)}+\dfrac{\sin(x)}{\cos(x)}&\small{\text{; définition de }\tan(x)\text{ et }\sec(x)}\\[1em]=\dfrac{1+\sin(x)}{\cos(x)}&\\[1em]=\dfrac{(1+\sin(x))}{\cos(x)}\cdot\dfrac{(1-\sin(x))}{(1-\sin(x))}&\small\text{; multiplication par le conjugué du numérateur}\\[1em]=\dfrac{1-\sin^2(x)}{\cos(x)(1-\sin(x))}&\small ;\;(1+\sin(x))(1-\sin(x))=1-\sin^2(x)\\[1em]=\dfrac{\cos^2(x)}{\cos(x)(1-\sin(x))}&\small{\text{; identité }\cos^2(x)=1-\sin^2(x)}\\[1em]=\dfrac{\cos(x)}{1-\sin(x)}&\small{\text{; simplication par }\cos(x)}\\&\square\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/80d42dfbb4522a79b791708da3433a77.png)
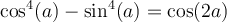
![\begin{array}{ll}\cos^4(a)-\sin^4(a)&\\[1em]=\left(\cos^2(a)+\sin^2(a)\right)\left(\cos^2(a)-\sin^2(a)\right)&\small\text{; il s'agit d'une différence de carrés}\\&\;\small u^2-v^2=(u+v)(u-v)\\&\small{\text{ où }u=\cos^2(a)\text{ et }v=\sin^2(a)}\\=(1)(\cos(2a))&\small{\text{; identités }\cos^2(a)+\sin^2(a)=1}\\&\;\small{\text{ et }\cos^2(a)-\sin^2(a)=\cos(2a)}\\=\cos(2a)&\\&\square\end{array} \begin{array}{ll}\cos^4(a)-\sin^4(a)&\\[1em]=\left(\cos^2(a)+\sin^2(a)\right)\left(\cos^2(a)-\sin^2(a)\right)&\small\text{; il s'agit d'une différence de carrés}\\&\;\small u^2-v^2=(u+v)(u-v)\\&\small{\text{ où }u=\cos^2(a)\text{ et }v=\sin^2(a)}\\=(1)(\cos(2a))&\small{\text{; identités }\cos^2(a)+\sin^2(a)=1}\\&\;\small{\text{ et }\cos^2(a)-\sin^2(a)=\cos(2a)}\\=\cos(2a)&\\&\square\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c24d120c915717a8fab24a1f48730d6f.png)
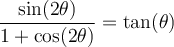
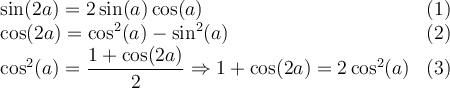
![\begin{array}{lll}\dfrac{\sin(2\theta)}{1+\cos(2\theta)}&=\dfrac{2\sin(\theta)\cos(\theta)}{2\cos^2(\theta)}&\small\text{; identités (1) et (3)}\\[1em]&=\dfrac{\sin(\theta)}{\cos(\theta)}&\small{\text{; simplification par }2\cos(\theta)}\\[1em]&=\tan(\theta)&\small\text{; définition de tangente}\\&&\square\end{array} \begin{array}{lll}\dfrac{\sin(2\theta)}{1+\cos(2\theta)}&=\dfrac{2\sin(\theta)\cos(\theta)}{2\cos^2(\theta)}&\small\text{; identités (1) et (3)}\\[1em]&=\dfrac{\sin(\theta)}{\cos(\theta)}&\small{\text{; simplification par }2\cos(\theta)}\\[1em]&=\tan(\theta)&\small\text{; définition de tangente}\\&&\square\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/75a941aaa5e7415643a9239a7667264f.png)