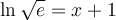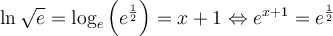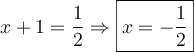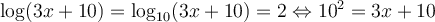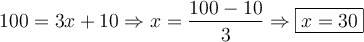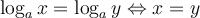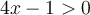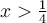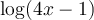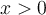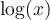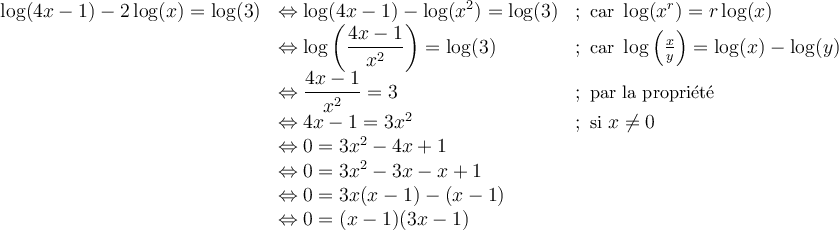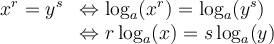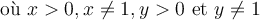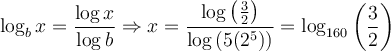2.5 Fonctions exponentielles et logarithmiques
- Introduction
- Fonction exponentielle
- Nombre d'Euler
- Logarithme et ses propriétés
- Table des logarithmes décimaux
- Fonction logarithmique
- Équations contenant des fonctions exponentielles et logarithmiques
7. Équations contenant des fonctions exponentielles et logarithmiques
Dans une équation exponentielle, la variable qui se retrouve en exposant ne peut pas être isolée à l'aide des opérations arithmétiques de base 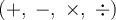 . De même, lorsqu'une équation comporte un ou plusieurs logarithmes, il faut d'abord effectuer une transformation pour faire disparaître ce dernier. Voici différentes catégories d'équations contenant des expressions exponentielles ou des logarithmes qui seront résolues dans cette page.
. De même, lorsqu'une équation comporte un ou plusieurs logarithmes, il faut d'abord effectuer une transformation pour faire disparaître ce dernier. Voici différentes catégories d'équations contenant des expressions exponentielles ou des logarithmes qui seront résolues dans cette page.
Nous aurons besoin des différentes propriétés des logarithmes vues dans les sections précédentes. Voici un tableau résumant ces propriétés.
Les équations contenant des expressions exponentielles qu'on peut ramener à une base commune
La propriété suivante dit que pour deux fonctions exponentielles égales, si les bases sont identiques, alors les exposants doivent être égaux.
Nous allons résoudre les équations suivantes à l'aide de cette propriété.
solution On peut exprimer 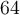 comme une puissance de
comme une puissance de 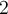 , ainsi :
, ainsi :

Les solutions de cette équation sont  et
et  .
.
solution Résoudre cette équation signifie isoler le  situé dans les exposants. Tout d'abord, il faut transformer les deux membres de l'égalité pour les mettre sur une base commune, soit
situé dans les exposants. Tout d'abord, il faut transformer les deux membres de l'égalité pour les mettre sur une base commune, soit 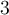 .
.
Les équations contenant des logarithmes
Nous avons vu qu'un logarithme n'est rien d'autre qu'un exposant. La définition de logarithme permet ainsi de transformer l'équation logarithmique en une équation exponentielle.
Cette égalité se traduit par la phrase suivante : « 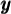 , le logarithme, est l'exposant que l'on doit attribuer à
, le logarithme, est l'exposant que l'on doit attribuer à 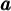 pour obtenir
pour obtenir 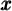 ».
».
Nous allons résoudre les équations suivantes à l'aide de cette définition.
solution On sait que
solution On sait que
Si les deux membres de l'égalité contiennent des logarithmes de même base, on peut utiliser la propriété de la fonction logarithmique suivante :
Nous allons résoudre l'équation 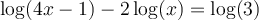 à l'aide de cette propriété.
à l'aide de cette propriété.
solution La solution de cette équation doit faire partie du domaine de l'équation, donc respecter les conditions suivantes :
Le domaine de l'équation est dont ![\left]\frac{1}{4},\infty\right[ \left]\frac{1}{4},\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7df16ac6a553c11ab9a673147f03a467.png) et la solution doit faire partie de ce domaine.
et la solution doit faire partie de ce domaine.
On résout l'équation de la façon suivante :
Les solutions de cette équation sont  et
et 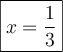 , car elles font parties du domaine.
, car elles font parties du domaine.
Les équations exponentielles que l'on peut résoudre à l'aide des logarithmes
Si l'on veut résoudre une équation contenant des exponentielles où il est impossible de trouver une base commune, il faut utiliser la propriété suivante :Nous allons résoudre l'équation 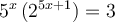 .
.
solution On ne peut pas trouver de base commune à 5 et 2. On utilise donc la propriété précédente en calculant le logarithme décimal à chaque membre de l'égalité.
La solution de l'équation est 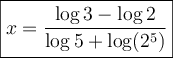 ou, en simplifiant à l'aide des propriétés des logarithmes,
ou, en simplifiant à l'aide des propriétés des logarithmes, 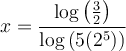 .
.
Pour le plaisir, on pourrait également exprimer cette solution à l'aide d'un seul logarithme en utilisant la formule de changement de base et le fait que 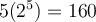 .
.
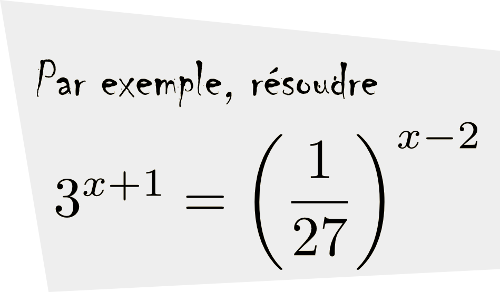
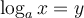
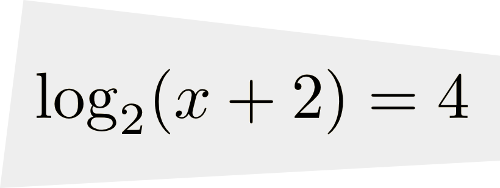
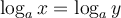
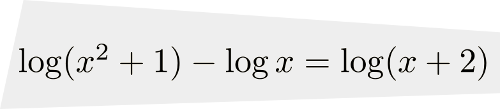
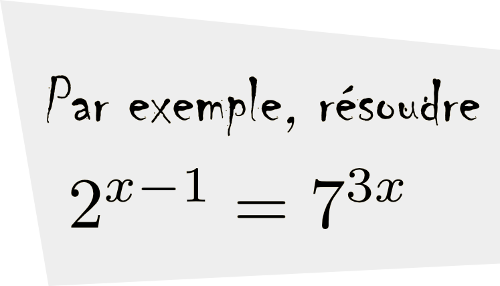
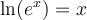
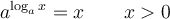
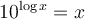
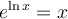
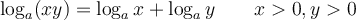
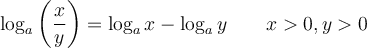

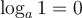
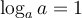
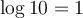
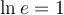
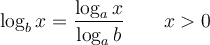
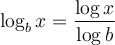
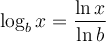
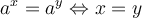
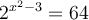
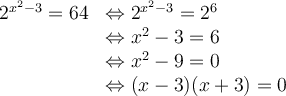
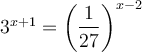
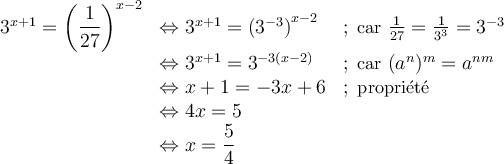
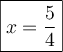
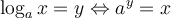
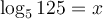
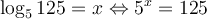
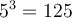
 b) Résoudre l'équation
b) Résoudre l'équation