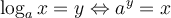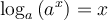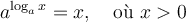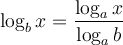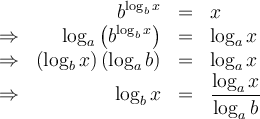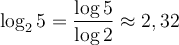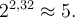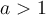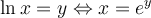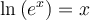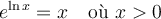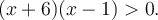2.5 Fonctions exponentielles et logarithmiques
- Introduction
- Fonction exponentielle
- Nombre d'Euler
- Logarithme et ses propriétés
- Table des logarithmes décimaux
- Fonction logarithmique
- Équations contenant des fonctions exponentielles et logarithmiques
6. Fonction logarithmique
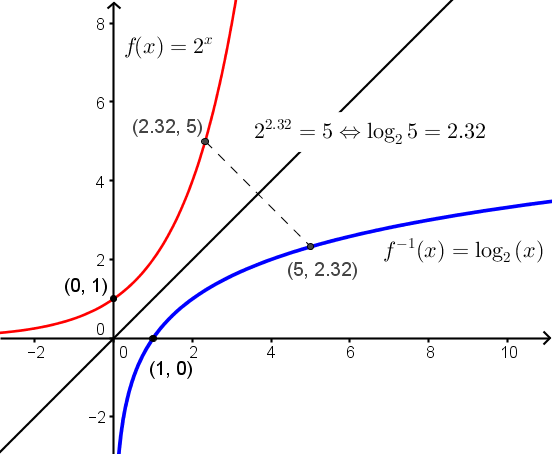
La fonction logarithmique est la fonction réciproque de la fonction exponentielle. Si 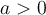 et
et 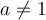 , la fonction exponentielle
, la fonction exponentielle 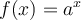 possède une fonction réciproque
possède une fonction réciproque 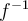 , qu'on appelle la fonction logarithmique de base
, qu'on appelle la fonction logarithmique de base 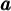 et que l'on note
et que l'on note 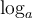 .
.
Par définition de la fonction réciproque, le graphique de la fonction logarithmique est la réflexion des points du graphique de la fonction exponentielle par rapport à la droite 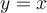 . Par conséquent, on aura :
. Par conséquent, on aura :
De plus, sachant que deux fonctions réciproques sont telles que 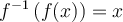 et
et 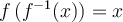 , on peut déduire deux autres propriétés des logarithmiques.
, on peut déduire deux autres propriétés des logarithmiques.
Ces deux dernières propriétés nous permettent de créer la formule de changement de base suivante :
Preuve :
La formule de changement de base est utile pour calculer, à l'aide de la calculatrice, des valeurs comme 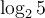 en utilisant le logarithme décimal
en utilisant le logarithme décimal 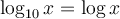 ou le logarithme naturel
ou le logarithme naturel 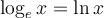 . En effet,
. En effet,
Représentations des fonctions logarithmiques
Il existe deux types de fonctions logarithmiques 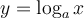 , celles pour lesquelles
, celles pour lesquelles 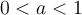 et celles pour lesquelles
et celles pour lesquelles 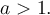 À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions logarithmiques pour ces différentes valeurs positives de
À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions logarithmiques pour ces différentes valeurs positives de  .
.
Toutes ces fonctions ont comme point commun 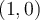 , car si l'exposant est
, car si l'exposant est  , alors
, alors
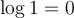 , car
, car 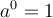
pour toutes valeurs positives de 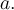
De plus, ![\text{dom }f = \left]{0, \infty}\right[ \text{dom }f = \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3002e546d7172a9563ec19bf9dd43cfc.png) . Cela signifie que la fonction possède une asymptote verticale, soit l'axe des
. Cela signifie que la fonction possède une asymptote verticale, soit l'axe des  . Finalement, il n'y a ni minimum, ni maximum, de sorte que l'image de la fonction est
. Finalement, il n'y a ni minimum, ni maximum, de sorte que l'image de la fonction est 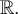
![]() Déplacez le curseur vertical à droite afin de noter l'effet sur le graphique de l'augmentation et de la diminution de la base
Déplacez le curseur vertical à droite afin de noter l'effet sur le graphique de l'augmentation et de la diminution de la base  .
.
Fonction logarithmique naturel 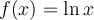
![]() Faites apparaître la fonction logarithmique
Faites apparaître la fonction logarithmique 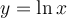 en cochant la case associée. La courbe représentant cette fonction est en vert. En déplaçant le curseur vertical pour que la courbe rouge se rapproche de plus en plus de la courbe verte, vous remarquez que la base
en cochant la case associée. La courbe représentant cette fonction est en vert. En déplaçant le curseur vertical pour que la courbe rouge se rapproche de plus en plus de la courbe verte, vous remarquez que la base  s'approche du nombre d'Euler
s'approche du nombre d'Euler 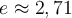 . Le logarithme naturel est en fait le logarithmique de base
. Le logarithme naturel est en fait le logarithmique de base 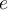 .
.
Ainsi, la fonction 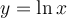 est la fonction réciproque de la fonction exponentielle
est la fonction réciproque de la fonction exponentielle 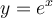 . On peut en déduire que
. On peut en déduire que
Le domaine de fonctions logarithmiques composées
Dans une section précédente, nous avons vu les conditions à respecter pour trouver le domaine d'une fonction composée. Cliquez sur ce lien si vous désirez vous rafraîchir la mémoire. Pour trouver le domaine d'une fonction composée, il faut tenir compte du domaine de chacune des fonctions qui la compose. Voici un exemple où la fonction logarithmique fait partie d'une de ces fonctions.
Trouvons le domaine de la fonction 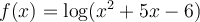 .
.
solution Puisque la fonction 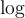 est définie seulement sur les réels positifs, c'est-à-dire sur
est définie seulement sur les réels positifs, c'est-à-dire sur ![\left]0,+\infty\right[ \left]0,+\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/8a44a3d914a6c2134c9bda0c382a20dd.png) , il faut que la fonction « à l'intérieur » du
, il faut que la fonction « à l'intérieur » du 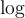 appartienne à cet intervalle.
appartienne à cet intervalle.
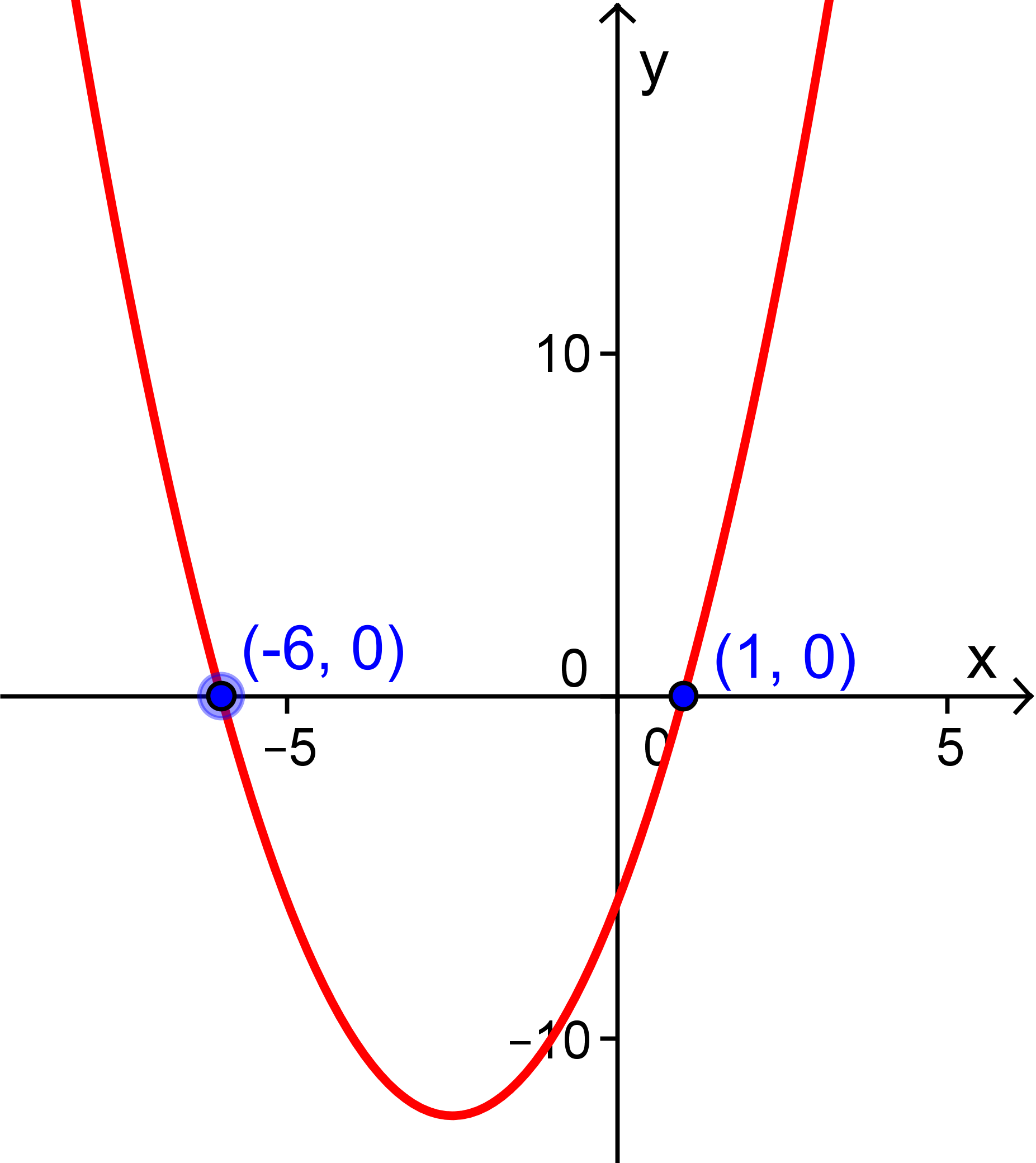
On peut exprimer notre fonction composée par  où
où 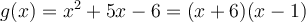 .
.
Ainsi, il faut trouver les valeurs de  pour que
pour que ![g(x)=(x+6)(x-1)\in\left]0,+\infty\right[ g(x)=(x+6)(x-1)\in\left]0,+\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/35e0e14a93be7832f85a539be77abf19.png) . Il faut donc résoudre l'inéquation
. Il faut donc résoudre l'inéquation
À partir du graphique de la fonction quadratique, on a que  est strictement positive si
est strictement positive si  et
et 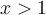 .
.
De plus, comme  est définie sur les réels, on a que le domaine de
est définie sur les réels, on a que le domaine de  est
est ![\left]-\infty,-6\right[\cup\left]1,+\infty\right[ \left]-\infty,-6\right[\cup\left]1,+\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3d5fab69bf73cd6fc7755a12066f239c.png) .
.