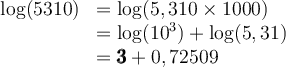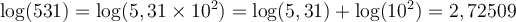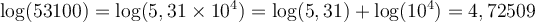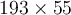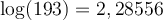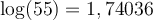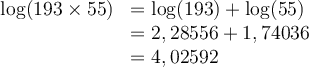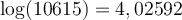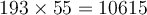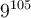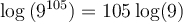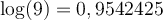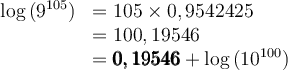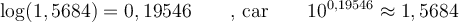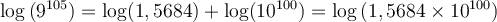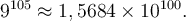2.5 Fonctions exponentielles et logarithmiques: Table des logarithmes décimaux

5. Table des logarithmes décimaux

Avant l'arrivée des calculatrices et des ordinateurs, il n'y a pas si longtemps d'ailleurs, on utilisait des tables de logarithmes pour faire des calculs périlleux comportant des multiplications, des divisions et des exposants.

Tout d'abord, étant donné que nous travaillons avec les logarithmes décimaux, on peut remarquer la caractéristique suivante :

Puissance de 10 inférieure à $x$ , la plus près	$x$	$\log(x)$
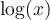10⁰ = 1	2	0,30103
10⁰ = 1	5	0,69897
10¹	12	1,07918
10¹	75	1,87506
10²	225	2,35218
	600	2,77815
	835	2,92168
10³	1200	3,07918
	5310	3,72509
	9420	3,97405

Par la propriété des logarithmes, si on prend par exemple le nombre 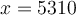$x = 5310$ , on aura

$\begin{array}{ll}\log(5310)&=\log(5,310\times1000)\\&=\log(10^3)+\log(5,31)\\&=\pmb{3}+0,72509\end{array}$

Par conséquent, dans une table, le logarithme d'un nombre se compose de deux parties :

Une partie entière (3) qui indique l'ordre de grandeur du nombre $x$ : c'est la caractéristique. C'est aussi l'exposant de la puissance de 10 la plus près et inférieure à notre nombre.
Une partie décimale (0,72509), qui porte le nom de mantisse. C'est cette dernière qui est lue sur la table.

Par exemple, comme 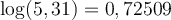$\log(5,31)=0,72509$ , on peut déduire les logarithmes de 531 et 53100.

$\log(531)=\log(5,31\times 10^2)= \log(5,31)+\log(10^2)=2,72509$

$\log(53100)=\log(5,31\times 10^4)=\log(5,31)+\log(10^4)=4,72509$

a) Calculons le produit suivant :

$193 \times 55$

Si $\log(193) = 2,28556$ et $\log(55)=1,74036$ , alors

$\begin{array}{ll}\log(193\times55)&=\log(193) + \log(55)\\&=2,28556 + 1,74036\\&=4,02592\end{array}$

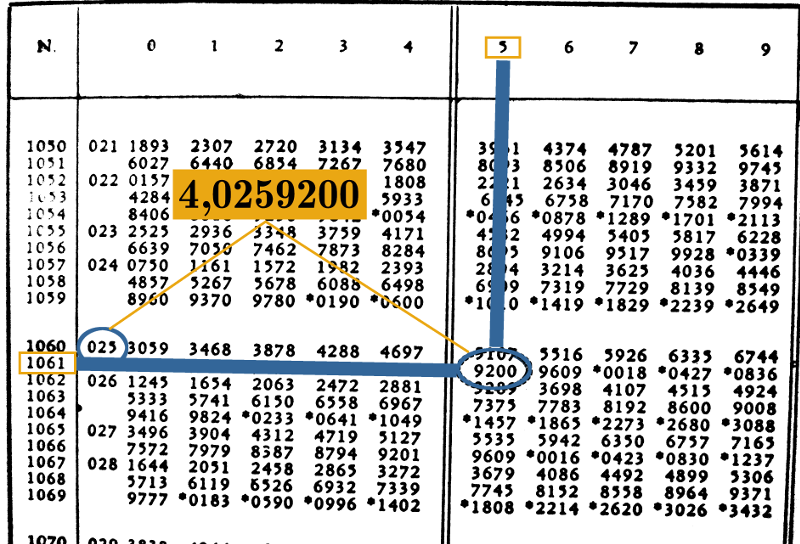
En lisant sur une table de logarithmes, on trouve que

$\log(10615) = 4,02592$

On peut ainsi conclure que

$193 \times 55=10615$

b) Donnons une approximation du nombre

$9^{105}$

À la calculatrice, ce calcul est impossible, mais en utilisant les propriétés des logarithmes, on peut approximer ce nombre. En effet,

$\log\left({9^{105}}\right)=105\log(9)$

Comme $\log(9)=0,9542425$ , alors

$\begin{array}{rl}\log\left({9^{105}}\right)&=105\times0,9542425\\&=100,19546\\&=\pmb{0,19546}+\log\left({10^{100}}\right)\end{array}$

Pour trouver notre nombre, on va avoir besoin de trouver le nombre dont le logarithme correspond à 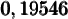$\pmb{0,19546}$ . En lisant sur une table de logarithme, on trouve que

$\log(1,5684)=0,19546 \qquad \text{, car} \qquad 10^{0,19546} \approx 1,5684$

On peut donc conclure que

$\log\left({9^{105}}\right)=\log(1,5684) + \log(10^{100})=\log\left({1,5684\times10^{100}}\right)$

et donc

$9^{105}\approx 1,5684\times10^{100}.$