2.5 Fonctions exponentielles et logarithmiques
- Introduction
- Fonction exponentielle
- Nombre d'Euler
- Logarithme et ses propriétés
- Table des logarithmes décimaux
- Fonction logarithmique
- Équations contenant des fonctions exponentielles et logarithmiques
4. Logarithme et ses propriétés
Les origines du logarithme

John Napier
Au XVIe siècle, les calculatrices n'existaient évidemment pas encore et les nombres décimaux n'étaient pas d'usage courant. Pourtant, l'astronomie, la navigation et le commerce demandaient d'effectuer des opérations de plus en plus complexes avec des nombres très élevés. C'est ainsi que le mathématicien John Napier, aussi connu sous le nom francisé de Neper, publie en 1614 un outil permettant de simplifier les calculs opératoires : le logarithme.
Au départ, Neper a développé les logarithmes pour simplifier les calculs de trigonométrie utiles en astronomie. Il donne ainsi une première table des logarithmes des sinus d'angles. L'astronome écossais Jost Bürgi aurait également inventé les logarithmes au même moment et indépendamment, mais sa publication est postérieure.
Toutefois, les logarithmes ne trouveront leur essor dans la communauté scientifique qu'après la mort de Napier. Le mathématicien anglais Henry Briggs (1561-1630) imagina un autre système de logarithmes en base 10, aussi appelés logarithmes vulgaires ou décimaux, qui seront rapidement adoptées par tous.
Pour comprendre comment fonctionnait ces calculs, il faut d'abord définir les logarithmes.Commençons avec le logarithme en base 10. On décida de définir les logarithmes décimaux, noté 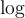 , comme les exposants de 10. Ainsi,
, comme les exposants de 10. Ainsi,
Par exemple,
On comprend bien cette définition avec des puissances positives et négatives de 10, mais 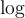 ne donne pas nécessairement une valeur entière. Par exemple,
ne donne pas nécessairement une valeur entière. Par exemple,
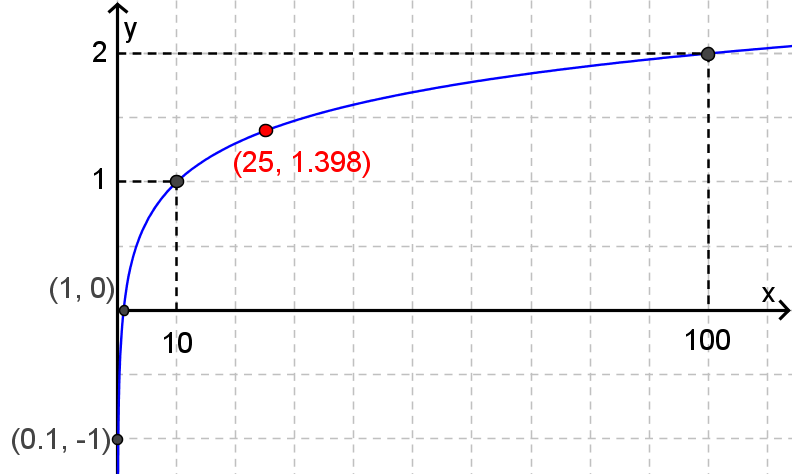
Si log(10) = 1 et log(100) = 2, alors on imagine que pour tout nombre  situé entre 10 et 100, log(x) est situé entre 1 et 2. En effet, log(25) = 1,397...
situé entre 10 et 100, log(x) est situé entre 1 et 2. En effet, log(25) = 1,397...
Ainsi, log est une fonction qui associe une valeur log(x) (l'exposant de 10) à chaque valeur de  donnée. On peut construire la courbe représentative de la fonction logarithmique de base 10 pour les valeurs de
donnée. On peut construire la courbe représentative de la fonction logarithmique de base 10 pour les valeurs de  strictement positives.
strictement positives.
Propriétés des logarithmes
L'idée de départ de l'utilisation des logarithmes était de remplacer les multiplications par des additions et les divisions par des soustractions afin de faciliter, rappelons-le, les calculs astronomiques à une époque où tout se faisait manuellement. Observons le tableau suivant.

La dernière ligne représente ce qu'on appelle une progression géométrique de raison 10 (101, 102, 103, 104) et la première ligne représente plutôt une progression arithmétique de raison 1 (1, 2, 3, 4). Tout simplement, lorsqu'on multiplie des puissances de 10 ensemble, il existe un lien d'addition entre leurs exposants. C'est ce que représente la propriété des exposants suivante :
Par exemple, on sait que log(10)=1, log(102)=2 et log(103)=3. On peut donc écrire
De plus, on sait que 103 = 10 × 102. Alors on peut conclure que
On peut généraliser cette propriété pour tout nombre réel positif et on peut également en déduire une propriété équivalente pour les soustractions de log.
On peut aussi déduire d'autres propriétés tout aussi importantes à partir de ces dernières.
Voici quelques exemples d'applications des propriétés précédentes.
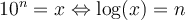

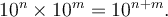
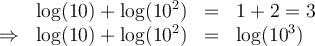
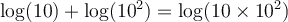

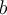
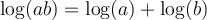
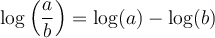
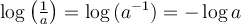
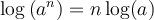
![\log\left({\sqrt[n]{a}}\right)=\dfrac{1}{n}\log(a) \log\left({\sqrt[n]{a}}\right)=\dfrac{1}{n}\log(a)](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2b0a33480737704c262c9df58e21cff0.png)
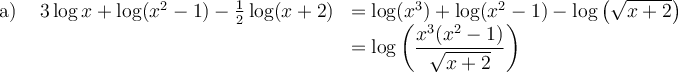
![\begin{array}{lrlr}\text{b) }&\dfrac{\log 5}{\log 100}+\log 1 &= \dfrac{\log 5}{\log_{10}(10^2)}+\log_{10}(10^0)&;\small\text{ attention: } \frac{\log a}{\log b}\neq\log a-\log b \\[0.8em]&&= \dfrac{\log 5}{2} + 0&\\[0.8em] &&=\frac{1}{2}(\log 5)&\\[0.8em]&&=\log\sqrt{5}&\end{array} \begin{array}{lrlr}\text{b) }&\dfrac{\log 5}{\log 100}+\log 1 &= \dfrac{\log 5}{\log_{10}(10^2)}+\log_{10}(10^0)&;\small\text{ attention: } \frac{\log a}{\log b}\neq\log a-\log b \\[0.8em]&&= \dfrac{\log 5}{2} + 0&\\[0.8em] &&=\frac{1}{2}(\log 5)&\\[0.8em]&&=\log\sqrt{5}&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/aa70f475b624d0bc12826d7497e0f1e5.png)
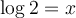
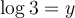

![\begin{array}{lrl}\text{a) }&\log\dfrac{8}{9}&=\log 8-\log 9\\[0.8em]&&=\log 2^3-\log 3^2\\[0.8em]&&=3\log 2 - 2\log 3\\[0.8em]&&=3x-2y \end{array} \begin{array}{lrl}\text{a) }&\log\dfrac{8}{9}&=\log 8-\log 9\\[0.8em]&&=\log 2^3-\log 3^2\\[0.8em]&&=3\log 2 - 2\log 3\\[0.8em]&&=3x-2y \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d5277db2aeb0f8c90362287e5fd1596a.png)
![\begin{array}{lrlr}\text{b) }&\log\sqrt{120}&=\dfrac{1}{2}\log(4\times 3\times 10)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 4 + \log 3 + \log 10\right)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 2^2 +\log 3 + 1\right)&;\small\text{ car } \log_{10} 10 = 1\\[0.8em]&&=\dfrac{1}{2}\left(2\log 2+\log 3 + 1\right)&\\[0.8em]&&=\dfrac{1}{2}\left(2x+y+1\right)& \end{array} \begin{array}{lrlr}\text{b) }&\log\sqrt{120}&=\dfrac{1}{2}\log(4\times 3\times 10)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 4 + \log 3 + \log 10\right)&\\[0.8em]&&=\dfrac{1}{2}\left(\log 2^2 +\log 3 + 1\right)&;\small\text{ car } \log_{10} 10 = 1\\[0.8em]&&=\dfrac{1}{2}\left(2\log 2+\log 3 + 1\right)&\\[0.8em]&&=\dfrac{1}{2}\left(2x+y+1\right)& \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/207262676be5906b140d4faeb60dc95b.png)