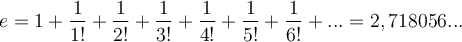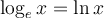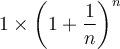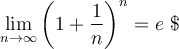2.5 Fonctions exponentielles et logarithmiques: Nombre d'Euler

3. Nombre d'Euler

Les applications du nombre $e$ sont variées. Au moyen de la fonction exponentielle, il est utilisé en économie (calcul des intérêts versés de façon continue), en biologie (mesure de la multiplication des cellules vivant dans un organisme), en sciences physiques, etc.

C'est le mathématicien Leonhard Euler qui, en 1727, a choisi la lettre $e$ pour désigner cette constante. Même s'il s'agit de l'initiale de son nom, ce serait plutôt parce que e est la première lettre du mot exponentiel. Euler obtient une estimation de $e$ avec 18 décimales en utilisant la formule suivante :

$e=1+ \dfrac{1}{1!} +\dfrac{1}{2!}+\dfrac{1}{3!} + \dfrac{1}{4!}+\dfrac{1}{5!}+\dfrac{1}{6!}+... =2,718056...$

Si vous n'avez jamais vu le symbole « ! », il signifie factoriel, par exemple 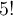$5!$ se dit « 5 factoriel » et est égal à $1 \times 2 \times 3 \times 4 \times 5 = 120$ .

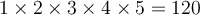Mais bien avant les études d'Euler sur le nombre $e$ , ce nombre fabuleux fit sa première apparition en 1618, dans un livre de John Napier, qui traitait des logarithmes. Eh oui, les logarithmes étaient pour les mathématiciens et scientifiques de cette époque bien plus intéressants à étudier, car ils facilitaient les calculs astronomiques qu'ils devaient faire. C'est pourquoi $e$ n'était pas en lui-même le centre d'intérêt. Ce livre définissait $e$ comme la base du logarithmique naturel qui, dans le langage d'aujourd'hui, est défini de la façon suivante :

$\log_{e}x = \ln{x}$

À cette époque, on ne remarqua par les merveilleuses possibilités du nombre $e$ . Ce n'est que plusieurs années plus tard, précisément en 1683, que Jacob Bernoulli, un mathématicien qui s'intéressait à la finance et aux intérêts composés, donna une première estimation de $e$ à l'aide du concept de limite (cette notion est abordée dans le cours Calcul différentiel).

L'activité suivante vous permettra de comprendre cette estimation.

Un placement d'argent à la banque engendre des intérêts composés lorsque, à la fin de chaque période, les intérêts sont ajoutés au placement afin de générer de nouveaux intérêts.

Même si ce n'est pas représentatif de la réalité, si l'on investit une somme de 1 $ à un taux d'intérêt annuel de 100 % et si les intérêts sont calculés une fois par année, la valeur de ce placement à la fin de l'année est de :

1 $ × 2 = 2 $

Vous avez fait 1 $ d'intérêt sur votre 1 $ de placement.

Mais si les intérêts annuels de 100 % sont calculées 2 fois par année (aux 6 mois), la valeur du placement à la fin de l'année se calcule ainsi :

après 6 mois : 1 $ + 1 × 50 % = 1 + 0,5 = 1,50 $
après 12 mois : 1,50 $ + 1,50 × 50 % = 1,50 (1 + 0,5) = 1,50 × 1,5 = 2,25 $

Au total, la somme accumulée sera de 1 $ × 1,5 × 1,5 = 2,25 $

Complétez maintenant le tableau suivant :

Nombre de périodes par années	Taux d'intérêt calculé à chaque période (%)	Calcul	Valeur du placement à la fin de l'année ($)
1 (annuellement)	100	1 × 2	2 $
2 (semestriellement)	50	1 × 1,5²	2,25 $
4 (trimestriellement)	25	1 × 1,25⁴	$
12 (mensuellement)			$
52 (chaque semaine)			$
365 (chaque jour)			$
8760 (chaque heure)			$
$n$	$\dfrac{100}{n}$	$1 \times \left({1+\dfrac{1}{n}}\right)^n$

Vous pouvez comparer vos réponses avec l'application Geogebra suivante :

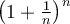Elle évalue l'expression de la dernière ligne pour différentes valeurs de n. Déplacez le curseur n afin de faire augmenter sa valeur ou, tout simplement, entrez la valeur de n désirée dans le champ de saisie. De quelle valeur l'expression $\left({1+\frac{1}{n}}\right)^n$ se rapproche-t-elle lorsque la valeur de n est de plus en plus grande ?

La réponse est le nombre d'Euler 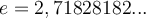$e = 2,71828182...$

En effet, si l'on investit une somme de 1 $ à un taux d'intérêt annuel de 100 % et que les intérêts sont calculés de façon continue, cela signifie que n prend des valeurs infiniment grandes, ainsi la valeur de notre placement à la fin de l'année sera :

$\lim \limits_{n\to \infty}\left({1+\dfrac{1}{n}}\right)^n=e \text{ \$}$

Pour terminer, voici un extrait du « Théorème du perroquet », un roman de Denis Guedj publié en 1998 et qui illustre bien cette dernière représentation du nombre $e$ :

« Suppose qu'il y a un an tu aies amassé un beau pécule qui nous permettra de payer notre voyage pour Manaus. Soit P, ce pécule. Tu l'as placé en attendant. Coup de bol, ton banquier t'a proposé un taux d'intérêt mirobolant : 100 % ! Ne rigole pas, ça s'est vu. Pas avec les pauvres, mais avec les riches. Rêve ! Calcule ! Au bout d'un an, tu aurais eu P + P = 2P. Tu aurais doublé ton pécule.
Si au lieu de toucher les intérêts à la fin de l'année, tu les avais touchés tous les six mois et que tu les aies replacés, au bout d'un an ça t'aurait fait P(1 + 1/2)². Calcule ! Tu aurais plus que doublé ton pécule tu aurais 2,25P. Si au lieu de toucher les intérêts tous les six mois, tu les avais touchés tous les trimestres et que tu les aies replacés, au bout de l'année, ça t'aurait fait P(1 + 1/4)⁴. Calcule ! Tu aurais gagné encore plus : 2,441P. Si tu les avais touchés tous les mois et que tu les aies replacés, ça t'aurait fait P(l + 1/12)¹². Calcule ! 2, 596. Encore plus ! Puis, tous les jours : P(1 + 1/365)³⁶⁵. Encore plus toutes les secondes, encore plus. Et puis, tous les riens du tout, « en continu ». Tu n'en peux plus, tu t'envoles, tu planes, tu te dis que c'est Byzance, que ton pécule pécuple, qu'il va quadrupler, décupler, centupler, millionupler, milliardupler, [ ... ] Tes intérêts composés, ils ont beau se décomposer, eh bien, à l'arrivée, tu n'as même pas le triple de ton pécule, ni même 2,9 fois plus, ni même 2,8 fois plus, ni même 2,75 fois plus, ni même 2,72 fois plus... Tu as seulement 2, 71 828 1828 ! ... Mon pauvre John, après toute cette richesse, te voilà seulement e fois moins pauvre qu'au départ ! »