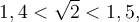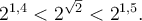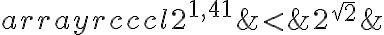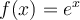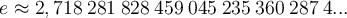2.5 Fonctions exponentielles et logarithmiques
- Introduction
- Fonction exponentielle
- Nombre d'Euler
- Logarithme et ses propriétés
- Table des logarithmes décimaux
- Fonction logarithmique
- Équations contenant des fonctions exponentielles et logarithmiques
2. Fonction exponentielle
Les fonctions exponentielles peuvent décrire plusieurs phénomènes importants en mathématiques appliquées et sont notamment utilisées pour prévoir la taille d'une population, pour déterminer l'âge d'un objet ancien en archéologie, pour calculer la valeur d'une hypothèque, etc.
Qu'ont en commun ces phénomènes et pourquoi peuvent-ils être décrits selon un modèle exponentiel? Considérons la situation suivante :
Supposons qu'un troupeau d'éléphants double à tous les 6 ans. Si le troupeau compte 7 éléphants en 2010,
en 2016 (6 ans plus tard) la population du troupeau sera de 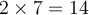 éléphants (elle aura doublé),
éléphants (elle aura doublé),
en 2022, la population du troupeau sera de 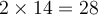 éléphants ou bien
éléphants ou bien 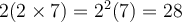 ,
,
en 2028, la population du troupeau sera de 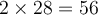 éléphants ou bien
éléphants ou bien 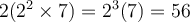 ,
,
...
après  période(s) de 6 années, la population du troupeau sera de
période(s) de 6 années, la population du troupeau sera de 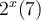 éléphants.
éléphants.
La variable  représente le temps et elle est l'exposant dans l'expression ci-dessus. Par conséquent, on dira que la population du troupeau d'éléphants varie en fonction du temps et selon un modèle exponentiel.
représente le temps et elle est l'exposant dans l'expression ci-dessus. Par conséquent, on dira que la population du troupeau d'éléphants varie en fonction du temps et selon un modèle exponentiel.
La population 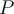 d'éléphants varie donc en fonction du temps
d'éléphants varie donc en fonction du temps  par un modèle exponentiel décrit par l'équation
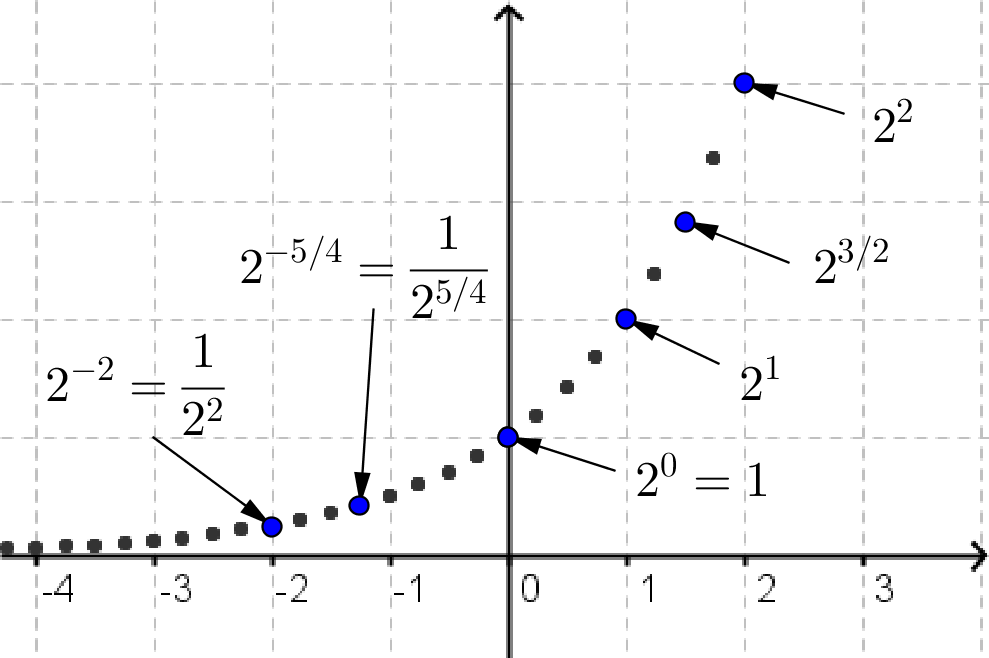
par un modèle exponentiel décrit par l'équation 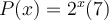 .
.
De façon générale,
Pour bien comprendre la fonction exponentielle et ses caractéristiques principales, il faut savoir manipuler adéquatement les propriétés des exposants entiers et rationnels. Dans cette section, nous faisons un rappel de ces propriétés, mais voici celles qui vous seront d'une grande utilité :
Par ces lois, on peut donner une explication logique à l'expression 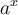 , où
, où 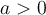 .
.
- Si l'exposant est un entier positif
 , alors
, alors 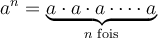 ;
; - Si l'exposant est un entier négatif
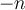 , alors
, alors 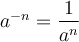 ;
; - Si l'exposant est un nombre rationnel
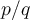 , où
, où 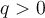 , alors
, alors ![a^{p/q}=\sqrt[q]{a^p}=\left({\sqrt[q]{a}}\right)^p a^{p/q}=\sqrt[q]{a^p}=\left({\sqrt[q]{a}}\right)^p](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9ebc8192f407efb646a4d8fbaf0c19f8.png) .
.
Cependant, si l'exposant est un nombre irrationnel, quelle explication peut-on donner ? Analysons plus en détails la fonction 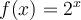 afin de répondre à cette question. Dans la figure ci-dessus, les trous dans le graphique sont en fait les valeurs de
afin de répondre à cette question. Dans la figure ci-dessus, les trous dans le graphique sont en fait les valeurs de 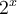 lorsque
lorsque  est un nombre irrationnel. Ainsi, ces valeurs sont comprises entre deux autres valeurs de
est un nombre irrationnel. Ainsi, ces valeurs sont comprises entre deux autres valeurs de 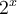 possédant des exposants rationnels.
possédant des exposants rationnels.
Par exemple, cherchons la valeur du nombre 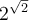 . On sait que
. On sait que
alors
Nous aurons de meilleures approximations de 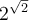 si nous prenons des valeurs rationnelles de
si nous prenons des valeurs rationnelles de  de plus en plus près de
de plus en plus près de 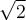 .
.
Représentations des fonctions exponentielles
Il existe deux types de fonctions exponentielles 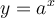 , celles dont
, celles dont 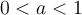 et celles dont
et celles dont 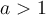 . À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions exponentielles pour différentes valeurs positives de
. À partir du graphique Geogebra suivant, étudions plus en détails les caractéristiques des fonctions exponentielles pour différentes valeurs positives de  .
.
Toutes ces fonctions ont comme point commun 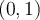 , car si l'exposant est
, car si l'exposant est  , alors
, alors
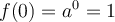
pour toute valeur positive de  .
.
- Si
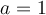 , la fonction obtenue est la droite horizontale
, la fonction obtenue est la droite horizontale 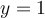 , car
, car 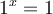 quelle que soit la valeur de l'exposant réel.
quelle que soit la valeur de l'exposant réel.
![]() Déplacez le curseur vertical à droite afin de remarquer l'effet obtenu sur le graphique en augmentant ou en diminuant la valeur de la base
Déplacez le curseur vertical à droite afin de remarquer l'effet obtenu sur le graphique en augmentant ou en diminuant la valeur de la base  .
.
- Si
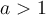 (au dessus de la ligne rose)
(au dessus de la ligne rose) - La fonction est croissante sur le domaine
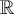 .
. - Les valeurs de
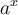 sont strictement positives, ainsi l'image est
sont strictement positives, ainsi l'image est![\left]{0, \infty}\right[ \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d13a6e4c304d2f4a427dad83ef19750a.png) . Cela signifie que la fonction possède l'axe des
. Cela signifie que la fonction possède l'axe des  comme asymptote horizontale.
comme asymptote horizontale. - Si
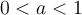
- On peut remarquer qu'étant donné que
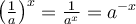 , le graphique de
, le graphique de 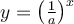 est une réflexion du graphique de
est une réflexion du graphique de 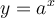 par rapport à l'axe des
par rapport à l'axe des  (voir la section : Transformations de fonctions).
(voir la section : Transformations de fonctions). - La fonction est décroissante sur le domaine
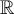 .
. - Son image est
![\left]{0,\infty}\right[ \left]{0,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6dd307f673b8f1b9fa5cdb6b6c78a955.png) .
.
Faites apparaître la fonction exponentielle 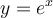
![]() en cochant la case associée. La courbe représentant cette fonction est en vert. Cette fonction possède des propriétés bien spéciales que nous explorons dans la section suivante.
en cochant la case associée. La courbe représentant cette fonction est en vert. Cette fonction possède des propriétés bien spéciales que nous explorons dans la section suivante.
![]() Pour l'instant, en déplaçant le curseur vertical pour déplacer la courbe rouge de plus en plus près de la courbe verte, vous obtenez une petite approximation de la valeur de cette base
Pour l'instant, en déplaçant le curseur vertical pour déplacer la courbe rouge de plus en plus près de la courbe verte, vous obtenez une petite approximation de la valeur de cette base  .
.
Vous remarquez que la valeur de 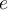 est très proche de
est très proche de 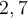 . En fait, ce nombre est irrationnel, donc son développement décimal n'est pas périodique. On l'appelle le nombre d'Euler et sa valeur approximative est :
. En fait, ce nombre est irrationnel, donc son développement décimal n'est pas périodique. On l'appelle le nombre d'Euler et sa valeur approximative est :
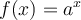
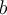
![\begin{array}{l@{ \hskip 5em}l} a^{x+y}=a^x a^y & a^{x-y}=\dfrac{a^x}{a^y} \\[0.8em] a^{xy}=\left({a^x}\right)^y & a^x b^x = \left({ab}\right)^x \end{array} \begin{array}{l@{ \hskip 5em}l} a^{x+y}=a^x a^y & a^{x-y}=\dfrac{a^x}{a^y} \\[0.8em] a^{xy}=\left({a^x}\right)^y & a^x b^x = \left({ab}\right)^x \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e4e8cb9218fd01ee954f1723be58274d.png)