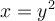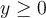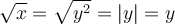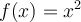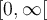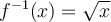2.4 Opérations sur les fonctions
- Introduction
- Transformation de fonctions
- Composition de fonctions
- Réciproque d'une fonction
4. Réciproque d'une fonction
On utilise la réciproque d'une fonction 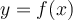 lorsqu'on veut exprimer la variable
lorsqu'on veut exprimer la variable  en fonction de la variable
en fonction de la variable  , c'est-à-dire :
, c'est-à-dire : 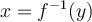 . Par contre, ce ne sont pas toutes les fonctions qui possèdent une fonction réciproque.
. Par contre, ce ne sont pas toutes les fonctions qui possèdent une fonction réciproque.
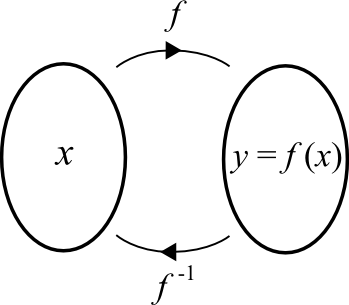
Comparons les deux diagrammes sagittaux des fonctions  et
et  ci-dessous. On observe que pour chaque valeur
ci-dessous. On observe que pour chaque valeur 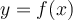 de l'ensemble B, on associe une seule valeur
de l'ensemble B, on associe une seule valeur  de l'ensemble A. Ce n'est pas le cas pour la fonction
de l'ensemble A. Ce n'est pas le cas pour la fonction  . En effet,
. En effet, 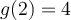 et
et 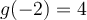 , ce qui implique qu'il existe deux valeurs de
, ce qui implique qu'il existe deux valeurs de  associées à la même valeur de
associées à la même valeur de  .
.
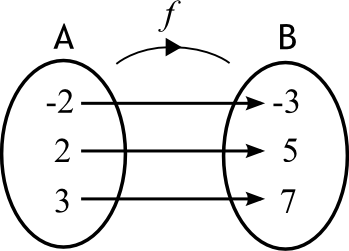
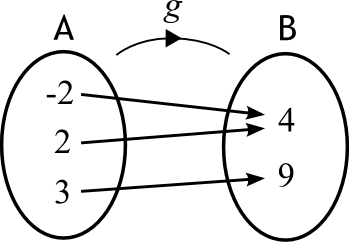
Ainsi, pour la fonction  , la relation qui associe les variables
, la relation qui associe les variables  de l'ensemble B aux variables
de l'ensemble B aux variables  de l'ensemble A ne respecte pas la définition d'une fonction.
de l'ensemble A ne respecte pas la définition d'une fonction.
On dira que  est une fonction injective, et donc possède une fonction réciproque, notée
est une fonction injective, et donc possède une fonction réciproque, notée 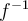 . La fonction
. La fonction  quant à elle n'est pas injective et ne possède donc pas de fonction réciproque.
quant à elle n'est pas injective et ne possède donc pas de fonction réciproque.
Nous pouvons maintenant définir la réciproque d'une fonction de la façon suivante :
Afin de trouver la règle de la fonction réciproque de  , il suffit de poser
, il suffit de poser 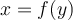 et d'isoler la variable
et d'isoler la variable  .
.
Exemple
Déterminons si la fonction 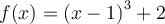 est injective. Si oui, trouvons la fonction réciproque de
est injective. Si oui, trouvons la fonction réciproque de  .
.
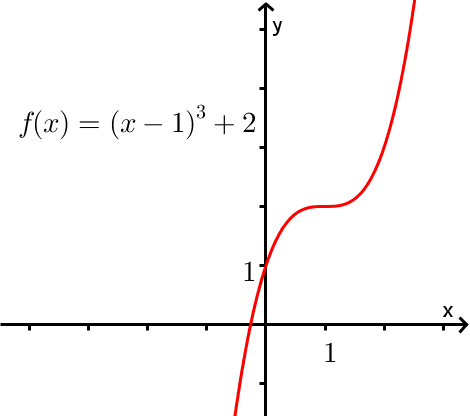
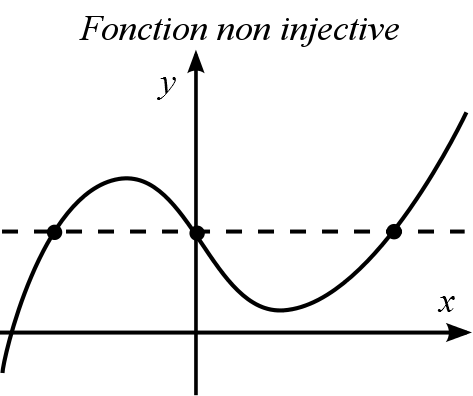
Pour toutes valeurs 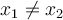 , on a que
, on a que 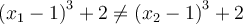 . En effet, en observant le graphique, on remarque que deux valeurs différentes de
. En effet, en observant le graphique, on remarque que deux valeurs différentes de  ne peuvent pas avoir la même image. De plus, le test de la droite horizontale confirme que
ne peuvent pas avoir la même image. De plus, le test de la droite horizontale confirme que  est injective.
est injective.
Afin de trouver la fonction réciproque de 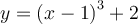 , procédons comme suit. Posons
, procédons comme suit. Posons
Isolons la variable  dans l'équation.
dans l'équation.
Ainsi, la fonction réciproque de  est définie par
est définie par ![f^{-1}(x)=\sqrt[3]{x-2}+1 f^{-1}(x)=\sqrt[3]{x-2}+1](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/30060d2f8a0d6cd3272e443aec2baeb0.png) .
.
De plus, la composition de la fonction  et de la fonction réciproque
et de la fonction réciproque 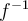 nous donne la formule de réciprocité souhaitée :
nous donne la formule de réciprocité souhaitée :
Remplacer  par
par  pour trouver la fonction réciproque est également la méthode utilisée pour obtenir le graphique de
pour trouver la fonction réciproque est également la méthode utilisée pour obtenir le graphique de 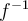 à partir du graphique de
à partir du graphique de  .
.
Soit un point 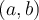 appartenant à la fonction
appartenant à la fonction  , alors par définition
, alors par définition 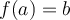 si et seulement
si et seulement 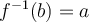 . Par conséquent le point
. Par conséquent le point 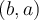 appartient à la fonction réciproque
appartient à la fonction réciproque 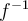 .
.
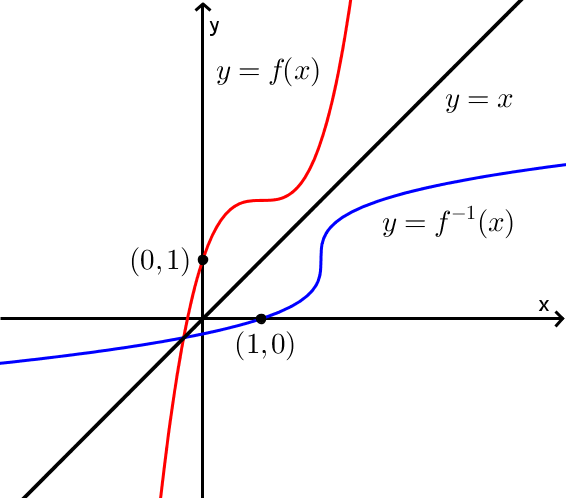
On remarque dans la figure ci-dessous que l'on obtient le point 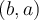 par une réflexion du point
par une réflexion du point 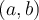 par rapport à la droite
par rapport à la droite 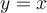 .
.
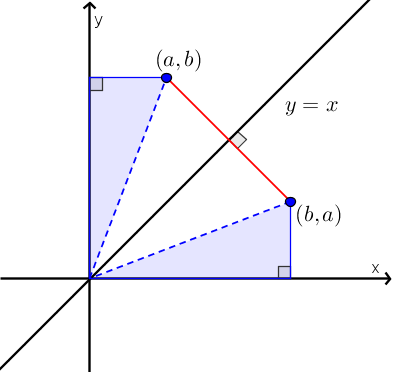
Donc,
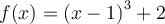 et de
et de ![f^{-1}(x)=\sqrt[3]{x-2}+1 f^{-1}(x)=\sqrt[3]{x-2}+1](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/30060d2f8a0d6cd3272e443aec2baeb0.png) .
.
Fonction racine carrée définie comme réciproque de la fonction quadratique
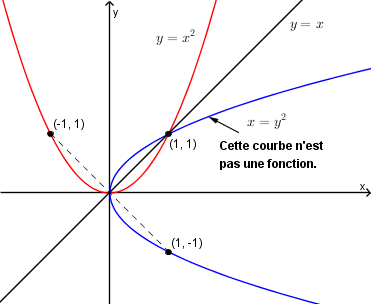
On remarque que la fonction quadratique 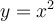 n'est pas une fonction injective sur son domaine, alors elle ne peut malheureusement pas avoir de fonction réciproque. En effet, pour une valeur de
n'est pas une fonction injective sur son domaine, alors elle ne peut malheureusement pas avoir de fonction réciproque. En effet, pour une valeur de  , il existe deux valeurs de
, il existe deux valeurs de  distinctes.
distinctes.
Par contre, si l'on définit 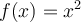 sur le domaine restreint
sur le domaine restreint 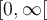 , elle possède alors une fonction réciproque déterminée ainsi :
, elle possède alors une fonction réciproque déterminée ainsi :
À partir du graphique Geogebra suivant, vous pouvez étudier la construction du graphique de la fonction 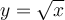 à partir de la fonction
à partir de la fonction 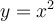 où
où 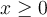 . Sa représentation correspond à la branche bleue de la parabole.
. Sa représentation correspond à la branche bleue de la parabole.
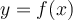
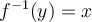
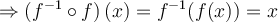
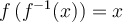
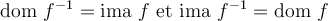
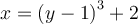
![\begin{array}{rll} x-2 &=&\left({y-1}\right)^3 \\ \left({x-2}\right)^{1/3} & =&y-1 \\ \sqrt[3]{x-2}+1 &=&y \end{array} \begin{array}{rll} x-2 &=&\left({y-1}\right)^3 \\ \left({x-2}\right)^{1/3} & =&y-1 \\ \sqrt[3]{x-2}+1 &=&y \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/5c68370abe26d6a4beac6fb85086ea36.png)
![\begin{array}{ll} (f^{-1} \circ f)(x) & = f^{-1}(f(x))\\ &=\sqrt[3]{\pmb{\Big({(x-1)^3+2}\Big)}-2}+1\\ &=\sqrt[3]{(x-1)^3}+1\\ &=x-1+1\\f^{-1}(f(x))&=x \end{array} \begin{array}{ll} (f^{-1} \circ f)(x) & = f^{-1}(f(x))\\ &=\sqrt[3]{\pmb{\Big({(x-1)^3+2}\Big)}-2}+1\\ &=\sqrt[3]{(x-1)^3}+1\\ &=x-1+1\\f^{-1}(f(x))&=x \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/383ad9188e18ad18285a37fa1ae1b7f1.png)