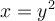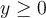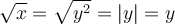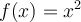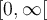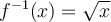2.4 Opérations sur les fonctions
| Site: | Mathéma-TIC |
| Cours: | Centre d'Aide en Mathéma-TIC (CAM-TIC) |
| Livre: | 2.4 Opérations sur les fonctions |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 18 mai 2024, 07:21 |
Description
- Introduction
- Transformation de fonctions
- Composition de fonctions
- Réciproque d'une fonction
1. Introduction
Dans cette section, nous allons étudier comment produire de nouvelles fonctions à partir des graphiques des fonctions de base en leur faisant subir des transformations diverses comme la translation, la déformation ou la réflexion.
On peut également combiner deux fonctions avec des opérations d'addition, de multiplication et de division ou bien en faire une fonction composée en prenant les images de la première fonction comme arguments pour la seconde.
2. Transformation de fonctions
En faisant subir certaines transformations aux graphiques des fonctions de base, on obtient les graphiques de fonctions de la même famille. Cela peut s'avérer utile lorsqu'on veut tracer rapidement le graphique de telles fonctions.
Les différentes transformations que nous allons étudier sont : la translation, la dilatation, la contraction et la réflexion. La nature de la transformation du graphique d'une fonction 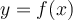 dépend des différents paramètres que l'on ajoute à sa règle initiale.
dépend des différents paramètres que l'on ajoute à sa règle initiale.
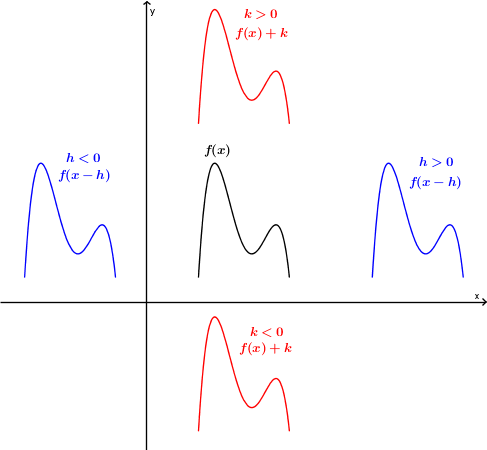
Translation
Voici le rôle que jouent les paramètres 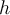 et
et 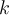 sur la translation du graphique de la fonction
sur la translation du graphique de la fonction 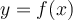 .
.
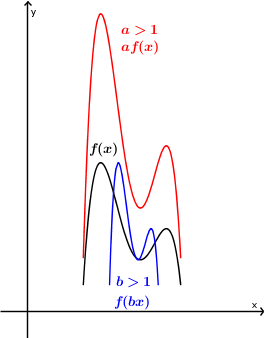
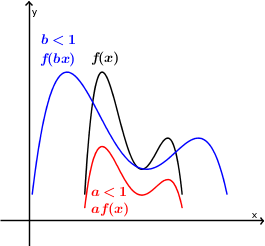
Contraction, dilatation et réflexion
Les paramètres  et
et 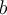 font subir au graphique de la fonction
font subir au graphique de la fonction 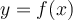 des transformations par dilatation, contraction et réflexion.
des transformations par dilatation, contraction et réflexion.
Si nous combinons les quatre paramètres dans une seule fonction, nous obtenons une fonction ayant pour règle
Le graphique de cette fonction se déduit du graphique de la fonction de base 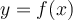 par la transformation
par la transformation
Exemples : À l'aide du graphique de la fonction de base associée, tracer les graphiques suivants.
Transformation des fonctions algébriques de base
Dans les sections précédentes, nous avons présenté les caractéristiques principales des graphiques de plusieurs fonctions algébriques, en utilisant l'application Geogebra. Vous pouvez explorer les effets des paramètres a, b, h et k sur ces graphiques en cliquant sur les liens.
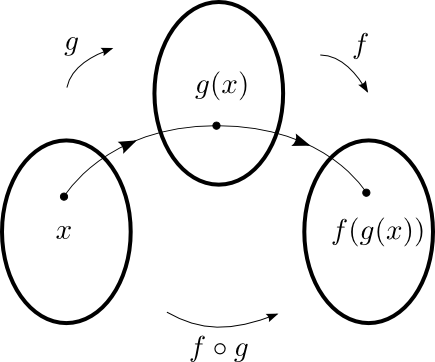
3. Composition de fonctions
La composition de fonctions est un processus qui combine deux fonctions pour en obtenir une nouvelle. La règle d'une fonction composée s'obtient par substitution.
Prenons, par exemple, deux fonctions  et
et  définies respectivement par
définies respectivement par 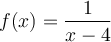 et
et 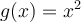 . Lorsqu'on veut calculer l'image de
. Lorsqu'on veut calculer l'image de 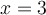 par la fonction composée de
par la fonction composée de  et
et  , il faut d'abord calculer l'image de
, il faut d'abord calculer l'image de 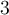 par la fonction
par la fonction  , soit
, soit 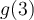 , et ensuite calculer l'image de
, et ensuite calculer l'image de 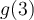 par la fonction
par la fonction  , soit
, soit 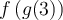 . Ainsi,
. Ainsi,
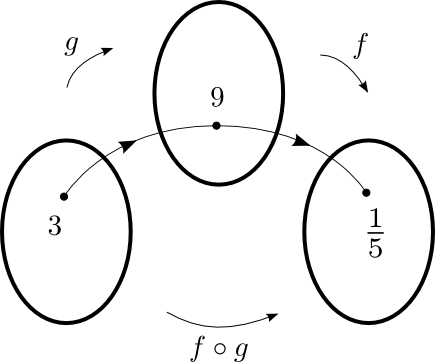
La règle de la fonction composée 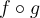 est obtenue en substituant
est obtenue en substituant 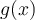 dans l'équation de la fonction
dans l'équation de la fonction  .
.
Domaine d'une fonction composée
Pour déterminer le domaine de la fonction composée 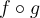 , il faut que
, il faut que  soit définie pour les valeurs de
soit définie pour les valeurs de  qu'on lui donne, et que
qu'on lui donne, et que  soit définie pour les valeurs de
soit définie pour les valeurs de 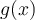 qu'on lui donne.
qu'on lui donne.
Ainsi, pour que 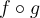 soit définie en
soit définie en  , c'est-à-dire que
, c'est-à-dire que 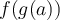 existe, il faut respecter ces deux conditions :
existe, il faut respecter ces deux conditions :
1.  doit appartenir au domaine de
doit appartenir au domaine de  .
.
2. 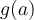 doit appartenir au domaine de
doit appartenir au domaine de  .
.
Dans l'exemple précédent, lorsque 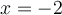 , on a
, on a 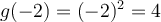 , mais
, mais 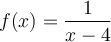 n'est pas définie en 4, car il y a division par zéro. Ainsi
n'est pas définie en 4, car il y a division par zéro. Ainsi 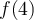 n'existe pas et par conséquent
n'existe pas et par conséquent 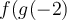 n'existe pas.
n'existe pas.
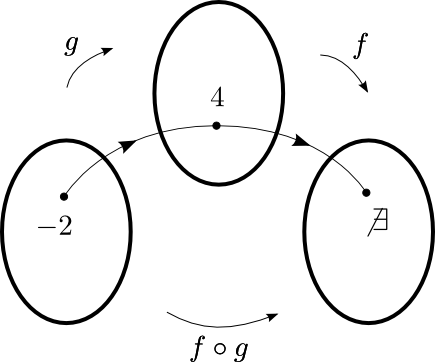
On a donc que 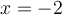 n'appartient pas au domaine de la fonction composée
n'appartient pas au domaine de la fonction composée 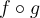 et, pour les mêmes raisons, on aura aussi que
et, pour les mêmes raisons, on aura aussi que 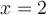 n'appartient pas au domaine.
n'appartient pas au domaine.
Exemple : Si 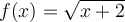 et
et 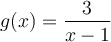 , déterminer la règle et le domaine des fonctions composées
, déterminer la règle et le domaine des fonctions composées 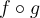 et
et 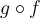 .
.
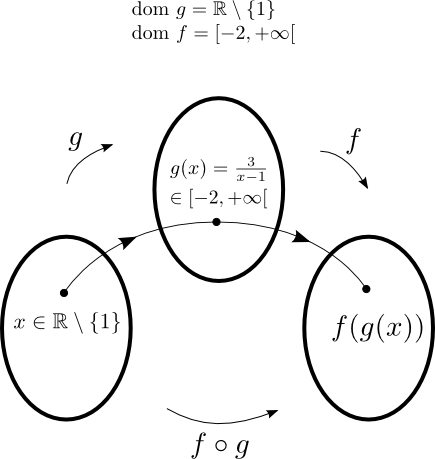
-
Pour que
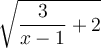 soit définie, il faut que
soit définie, il faut que 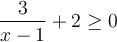 , c'est-à-dire que
, c'est-à-dire que 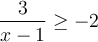 , donc que
, donc que 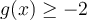 . Résolvons à l'aide d'un tableau de signes.
. Résolvons à l'aide d'un tableau de signes.![\left]{-\infty,-\frac{1}{2}}\right[ \left]{-\infty,-\frac{1}{2}}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6bdced3faa197713df8ff67e562708fc.png)
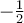
![\left]{-\frac{1}{2},1}\right[ \left]{-\frac{1}{2},1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7b5c92a264b02d14240a9f79a4081d52.png)

![\left]{1,\infty}\right[ \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1c8404c763714ff8de9f14e488b459df.png)
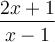



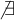

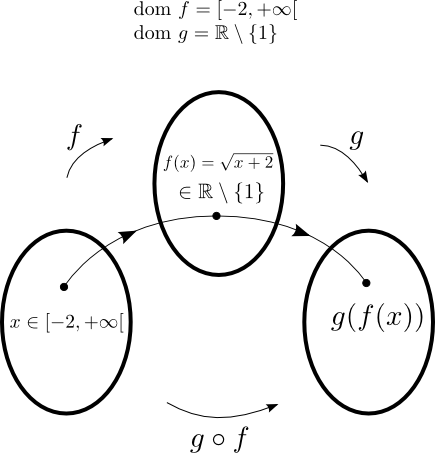
Par ce dernier exemple, nous pouvons remarquer que
À partir du graphique Geogebra ci-dessus, on remarque que le domaine d'une fonction composée n'est pas toujours ce que l'on croit.
On a que 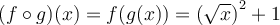 . En simplifiant, on obtient
. En simplifiant, on obtient 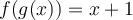 .
.
Or, on sait que le domaine de la droite 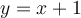 est :
est : 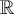 .
.
Pourtant, le domaine de la fonction composée 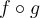 est :
est : 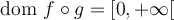 .
.
En effet, pour que  appartienne au domaine de
appartienne au domaine de 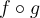 , il faut que
, il faut que
 appartienne au domaine de
appartienne au domaine de  , donc que
, donc que 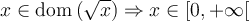 .
.
![]() En faisant bouger le point a sur le graphique de gauche, la trace de la fonction composée
En faisant bouger le point a sur le graphique de gauche, la trace de la fonction composée 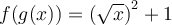 apparaît en bleue dans la fenêtre de droite pour créer la fonction linéaire
apparaît en bleue dans la fenêtre de droite pour créer la fonction linéaire 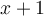 , mais seulement pour les valeurs de
, mais seulement pour les valeurs de 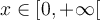 .
.
Exercices formatifs WeBWorK
 Fonction composée
Fonction composée
4. Réciproque d'une fonction
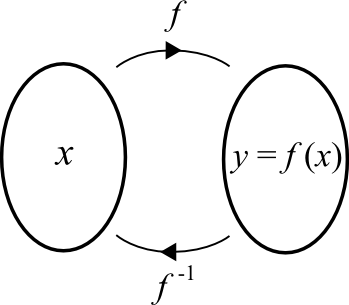
On utilise la réciproque d'une fonction 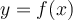 lorsqu'on veut exprimer la variable
lorsqu'on veut exprimer la variable  en fonction de la variable
en fonction de la variable  , c'est-à-dire :
, c'est-à-dire : 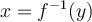 . Par contre, ce ne sont pas toutes les fonctions qui possèdent une fonction réciproque.
. Par contre, ce ne sont pas toutes les fonctions qui possèdent une fonction réciproque.
Comparons les deux diagrammes sagittaux des fonctions  et
et  ci-dessous. On observe que pour chaque valeur
ci-dessous. On observe que pour chaque valeur 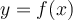 de l'ensemble B, on associe une seule valeur
de l'ensemble B, on associe une seule valeur  de l'ensemble A. Ce n'est pas le cas pour la fonction
de l'ensemble A. Ce n'est pas le cas pour la fonction  . En effet,
. En effet, 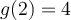 et
et 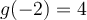 , ce qui implique qu'il existe deux valeurs de
, ce qui implique qu'il existe deux valeurs de  associées à la même valeur de
associées à la même valeur de  .
.
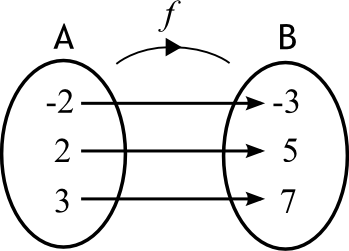
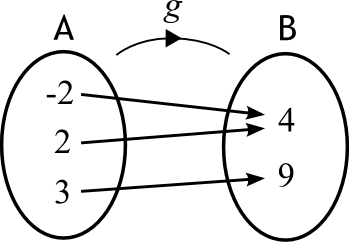
Ainsi, pour la fonction  , la relation qui associe les variables
, la relation qui associe les variables  de l'ensemble B aux variables
de l'ensemble B aux variables  de l'ensemble A ne respecte pas la définition d'une fonction.
de l'ensemble A ne respecte pas la définition d'une fonction.
On dira que  est une fonction injective, et donc possède une fonction réciproque, notée
est une fonction injective, et donc possède une fonction réciproque, notée 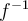 . La fonction
. La fonction  quant à elle n'est pas injective et ne possède donc pas de fonction réciproque.
quant à elle n'est pas injective et ne possède donc pas de fonction réciproque.
Nous pouvons maintenant définir la réciproque d'une fonction de la façon suivante :
Afin de trouver la règle de la fonction réciproque de  , il suffit de poser
, il suffit de poser 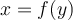 et d'isoler la variable
et d'isoler la variable  .
.
Exemple
Déterminons si la fonction 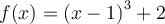 est injective. Si oui, trouvons la fonction réciproque de
est injective. Si oui, trouvons la fonction réciproque de  .
.
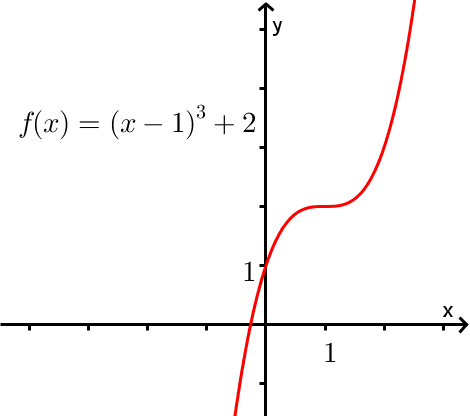
Pour toutes valeurs 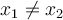 , on a que
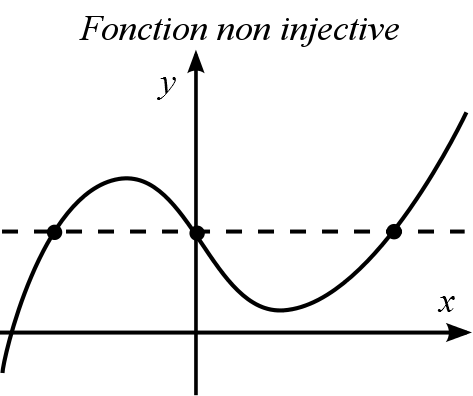
, on a que 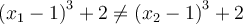 . En effet, en observant le graphique, on remarque que deux valeurs différentes de
. En effet, en observant le graphique, on remarque que deux valeurs différentes de  ne peuvent pas avoir la même image. De plus, le test de la droite horizontale confirme que
ne peuvent pas avoir la même image. De plus, le test de la droite horizontale confirme que  est injective.
est injective.
Afin de trouver la fonction réciproque de 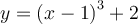 , procédons comme suit. Posons
, procédons comme suit. Posons
Isolons la variable  dans l'équation.
dans l'équation.
Ainsi, la fonction réciproque de  est définie par
est définie par ![f^{-1}(x)=\sqrt[3]{x-2}+1 f^{-1}(x)=\sqrt[3]{x-2}+1](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/30060d2f8a0d6cd3272e443aec2baeb0.png) .
.
De plus, la composition de la fonction  et de la fonction réciproque
et de la fonction réciproque 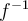 nous donne la formule de réciprocité souhaitée :
nous donne la formule de réciprocité souhaitée :
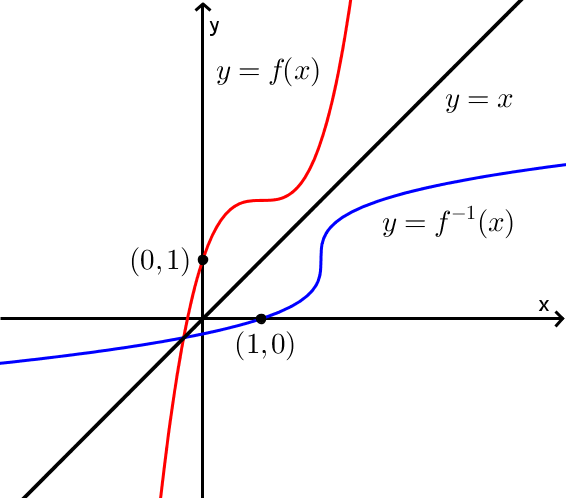
Remplacer  par
par  pour trouver la fonction réciproque est également la méthode utilisée pour obtenir le graphique de
pour trouver la fonction réciproque est également la méthode utilisée pour obtenir le graphique de 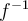 à partir du graphique de
à partir du graphique de  .
.
Soit un point 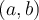 appartenant à la fonction
appartenant à la fonction  , alors par définition
, alors par définition 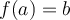 si et seulement
si et seulement 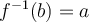 . Par conséquent le point
. Par conséquent le point 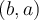 appartient à la fonction réciproque
appartient à la fonction réciproque 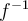 .
.
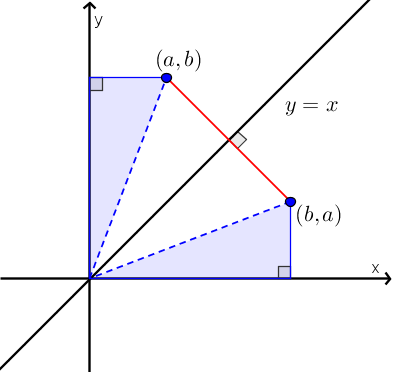
On remarque dans la figure ci-dessous que l'on obtient le point 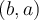 par une réflexion du point
par une réflexion du point 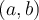 par rapport à la droite
par rapport à la droite 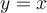 .
.
Donc,
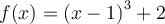 et de
et de ![f^{-1}(x)=\sqrt[3]{x-2}+1 f^{-1}(x)=\sqrt[3]{x-2}+1](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/30060d2f8a0d6cd3272e443aec2baeb0.png) .
.
Fonction racine carrée définie comme réciproque de la fonction quadratique
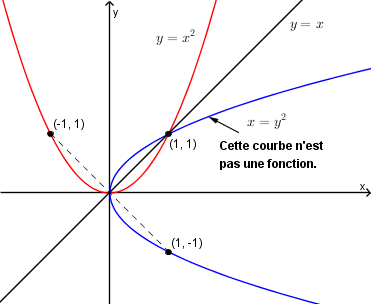
On remarque que la fonction quadratique 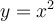 n'est pas une fonction injective sur son domaine, alors elle ne peut malheureusement pas avoir de fonction réciproque. En effet, pour une valeur de
n'est pas une fonction injective sur son domaine, alors elle ne peut malheureusement pas avoir de fonction réciproque. En effet, pour une valeur de  , il existe deux valeurs de
, il existe deux valeurs de  distinctes.
distinctes.
Par contre, si l'on définit 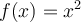 sur le domaine restreint
sur le domaine restreint 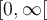 , elle possède alors une fonction réciproque déterminée ainsi :
, elle possède alors une fonction réciproque déterminée ainsi :
À partir du graphique Geogebra suivant, vous pouvez étudier la construction du graphique de la fonction 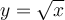 à partir de la fonction
à partir de la fonction 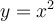 où
où 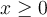 . Sa représentation correspond à la branche bleue de la parabole.
. Sa représentation correspond à la branche bleue de la parabole.
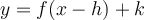
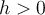
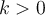
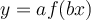
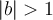
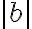
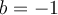
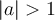

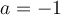
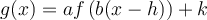
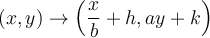
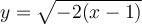
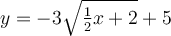

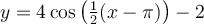
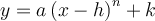
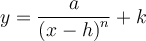
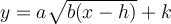
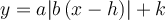
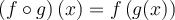
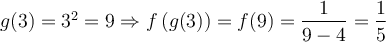
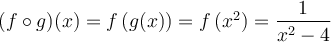
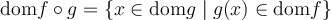
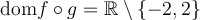
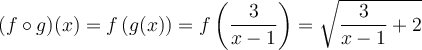
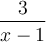
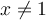
![\begin{array}{ll} \dfrac{3}{x-1} + 2 \geq 0 & \Leftrightarrow \dfrac{3 + 2(x-1)}{x-1} \geq 0 \\[0.8em] {} & \Leftrightarrow \dfrac{2x+1}{x-1} \geq 0 \end{array} \begin{array}{ll} \dfrac{3}{x-1} + 2 \geq 0 & \Leftrightarrow \dfrac{3 + 2(x-1)}{x-1} \geq 0 \\[0.8em] {} & \Leftrightarrow \dfrac{2x+1}{x-1} \geq 0 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2484a65c4ae3fa9378eb636d207fa47a.png)
![\left]{-\infty,-\frac{1}{2}}\right] \cup \left]{1,\infty}\right[ \left]{-\infty,-\frac{1}{2}}\right] \cup \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/db8a0350e61c8bb78f4dee954241e042.png)
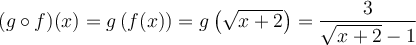
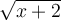

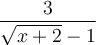
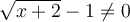
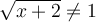
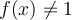
![\begin{array}{ll} \sqrt{x+2} \not= 1 & \Leftrightarrow \left({\sqrt{x+2}}\right)^2 \not= 1^2 \\[0.8em] {} & \Leftrightarrow x+2 \not= 1 \\[0.8em] {} & \Leftrightarrow x \not= -1 \end{array} \begin{array}{ll} \sqrt{x+2} \not= 1 & \Leftrightarrow \left({\sqrt{x+2}}\right)^2 \not= 1^2 \\[0.8em] {} & \Leftrightarrow x+2 \not= 1 \\[0.8em] {} & \Leftrightarrow x \not= -1 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9cd7581c56b748b043d223f4725721d6.png)
![\left[{-2,-1}\right[ \cup \left]{-1,\infty}\right[ \left[{-2,-1}\right[ \cup \left]{-1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e8d932bf40c90c3f6deccaf0942b363a.png)
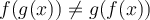
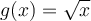
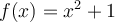
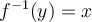
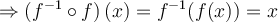
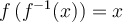
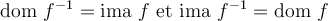
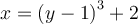
![\begin{array}{rll} x-2 &=&\left({y-1}\right)^3 \\ \left({x-2}\right)^{1/3} & =&y-1 \\ \sqrt[3]{x-2}+1 &=&y \end{array} \begin{array}{rll} x-2 &=&\left({y-1}\right)^3 \\ \left({x-2}\right)^{1/3} & =&y-1 \\ \sqrt[3]{x-2}+1 &=&y \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/5c68370abe26d6a4beac6fb85086ea36.png)
![\begin{array}{ll} (f^{-1} \circ f)(x) & = f^{-1}(f(x))\\ &=\sqrt[3]{\pmb{\Big({(x-1)^3+2}\Big)}-2}+1\\ &=\sqrt[3]{(x-1)^3}+1\\ &=x-1+1\\f^{-1}(f(x))&=x \end{array} \begin{array}{ll} (f^{-1} \circ f)(x) & = f^{-1}(f(x))\\ &=\sqrt[3]{\pmb{\Big({(x-1)^3+2}\Big)}-2}+1\\ &=\sqrt[3]{(x-1)^3}+1\\ &=x-1+1\\f^{-1}(f(x))&=x \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/383ad9188e18ad18285a37fa1ae1b7f1.png)