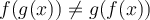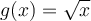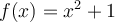2.4 Opérations sur les fonctions
- Introduction
- Transformation de fonctions
- Composition de fonctions
- Réciproque d'une fonction
3. Composition de fonctions
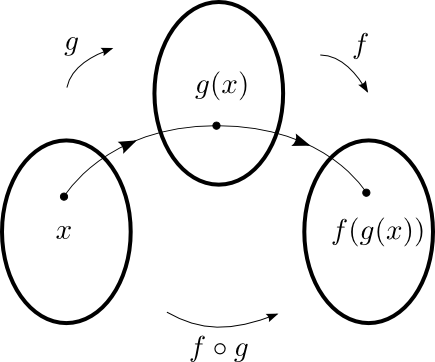
La composition de fonctions est un processus qui combine deux fonctions pour en obtenir une nouvelle. La règle d'une fonction composée s'obtient par substitution.
Prenons, par exemple, deux fonctions  et
et  définies respectivement par
définies respectivement par 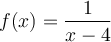 et
et 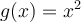 . Lorsqu'on veut calculer l'image de
. Lorsqu'on veut calculer l'image de 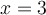 par la fonction composée de
par la fonction composée de  et
et  , il faut d'abord calculer l'image de
, il faut d'abord calculer l'image de 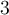 par la fonction
par la fonction  , soit
, soit 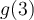 , et ensuite calculer l'image de
, et ensuite calculer l'image de 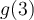 par la fonction
par la fonction  , soit
, soit 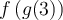 . Ainsi,
. Ainsi,
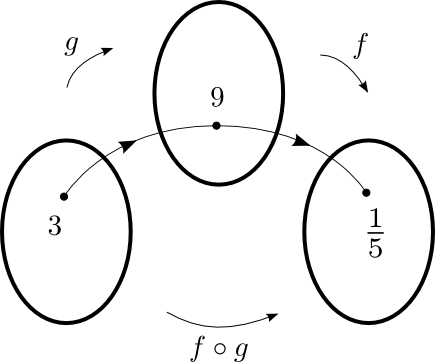
La règle de la fonction composée 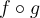 est obtenue en substituant
est obtenue en substituant 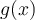 dans l'équation de la fonction
dans l'équation de la fonction  .
.
Domaine d'une fonction composée
Pour déterminer le domaine de la fonction composée 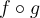 , il faut que
, il faut que  soit définie pour les valeurs de
soit définie pour les valeurs de  qu'on lui donne, et que
qu'on lui donne, et que  soit définie pour les valeurs de
soit définie pour les valeurs de 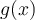 qu'on lui donne.
qu'on lui donne.
Ainsi, pour que 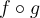 soit définie en
soit définie en  , c'est-à-dire que
, c'est-à-dire que 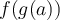 existe, il faut respecter ces deux conditions :
existe, il faut respecter ces deux conditions :
1.  doit appartenir au domaine de
doit appartenir au domaine de  .
.
2. 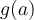 doit appartenir au domaine de
doit appartenir au domaine de  .
.
Dans l'exemple précédent, lorsque 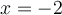 , on a
, on a 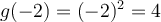 , mais
, mais 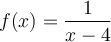 n'est pas définie en 4, car il y a division par zéro. Ainsi
n'est pas définie en 4, car il y a division par zéro. Ainsi 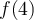 n'existe pas et par conséquent
n'existe pas et par conséquent 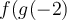 n'existe pas.
n'existe pas.
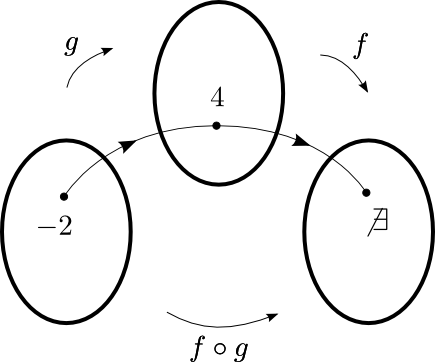
On a donc que 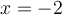 n'appartient pas au domaine de la fonction composée
n'appartient pas au domaine de la fonction composée 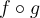 et, pour les mêmes raisons, on aura aussi que
et, pour les mêmes raisons, on aura aussi que 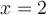 n'appartient pas au domaine.
n'appartient pas au domaine.
Exemple : Si 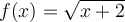 et
et 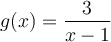 , déterminer la règle et le domaine des fonctions composées
, déterminer la règle et le domaine des fonctions composées 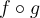 et
et 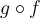 .
.
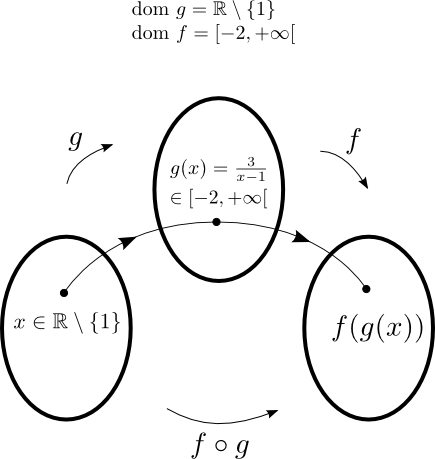
-
Pour que
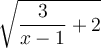 soit définie, il faut que
soit définie, il faut que 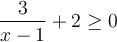 , c'est-à-dire que
, c'est-à-dire que 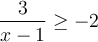 , donc que
, donc que 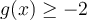 . Résolvons à l'aide d'un tableau de signes.
. Résolvons à l'aide d'un tableau de signes.![\left]{-\infty,-\frac{1}{2}}\right[ \left]{-\infty,-\frac{1}{2}}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6bdced3faa197713df8ff67e562708fc.png)
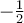
![\left]{-\frac{1}{2},1}\right[ \left]{-\frac{1}{2},1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7b5c92a264b02d14240a9f79a4081d52.png)

![\left]{1,\infty}\right[ \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1c8404c763714ff8de9f14e488b459df.png)
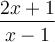



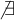

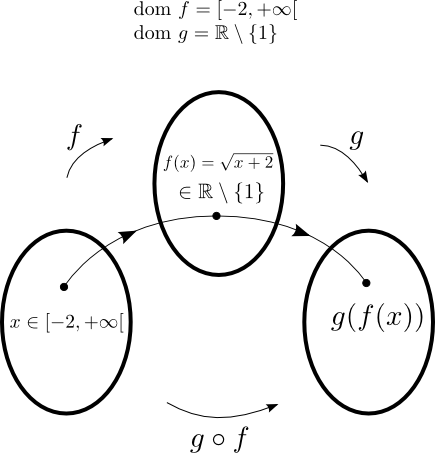
Par ce dernier exemple, nous pouvons remarquer que
À partir du graphique Geogebra ci-dessus, on remarque que le domaine d'une fonction composée n'est pas toujours ce que l'on croit.
On a que 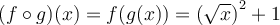 . En simplifiant, on obtient
. En simplifiant, on obtient 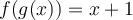 .
.
Or, on sait que le domaine de la droite 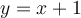 est :
est : 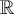 .
.
Pourtant, le domaine de la fonction composée 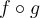 est :
est : 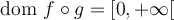 .
.
En effet, pour que  appartienne au domaine de
appartienne au domaine de 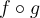 , il faut que
, il faut que
 appartienne au domaine de
appartienne au domaine de  , donc que
, donc que 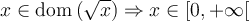 .
.
![]() En faisant bouger le point a sur le graphique de gauche, la trace de la fonction composée
En faisant bouger le point a sur le graphique de gauche, la trace de la fonction composée 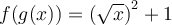 apparaît en bleue dans la fenêtre de droite pour créer la fonction linéaire
apparaît en bleue dans la fenêtre de droite pour créer la fonction linéaire 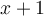 , mais seulement pour les valeurs de
, mais seulement pour les valeurs de 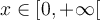 .
.
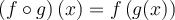
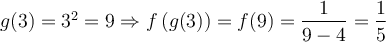
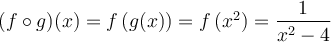
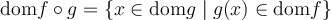
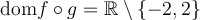
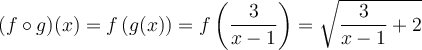
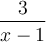
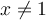
![\begin{array}{ll} \dfrac{3}{x-1} + 2 \geq 0 & \Leftrightarrow \dfrac{3 + 2(x-1)}{x-1} \geq 0 \\[0.8em] {} & \Leftrightarrow \dfrac{2x+1}{x-1} \geq 0 \end{array} \begin{array}{ll} \dfrac{3}{x-1} + 2 \geq 0 & \Leftrightarrow \dfrac{3 + 2(x-1)}{x-1} \geq 0 \\[0.8em] {} & \Leftrightarrow \dfrac{2x+1}{x-1} \geq 0 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2484a65c4ae3fa9378eb636d207fa47a.png)
![\left]{-\infty,-\frac{1}{2}}\right] \cup \left]{1,\infty}\right[ \left]{-\infty,-\frac{1}{2}}\right] \cup \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/db8a0350e61c8bb78f4dee954241e042.png)
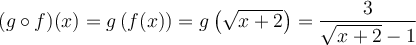
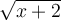

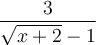
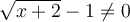
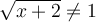
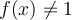
![\begin{array}{ll} \sqrt{x+2} \not= 1 & \Leftrightarrow \left({\sqrt{x+2}}\right)^2 \not= 1^2 \\[0.8em] {} & \Leftrightarrow x+2 \not= 1 \\[0.8em] {} & \Leftrightarrow x \not= -1 \end{array} \begin{array}{ll} \sqrt{x+2} \not= 1 & \Leftrightarrow \left({\sqrt{x+2}}\right)^2 \not= 1^2 \\[0.8em] {} & \Leftrightarrow x+2 \not= 1 \\[0.8em] {} & \Leftrightarrow x \not= -1 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9cd7581c56b748b043d223f4725721d6.png)
![\left[{-2,-1}\right[ \cup \left]{-1,\infty}\right[ \left[{-2,-1}\right[ \cup \left]{-1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e8d932bf40c90c3f6deccaf0942b363a.png)