2.3 Quelques fonctions particulières
- Fonction définie par parties ou par morceaux
- Fonction valeur absolue
- Fonctions paires et impaires
3. Fonctions paires et impaires
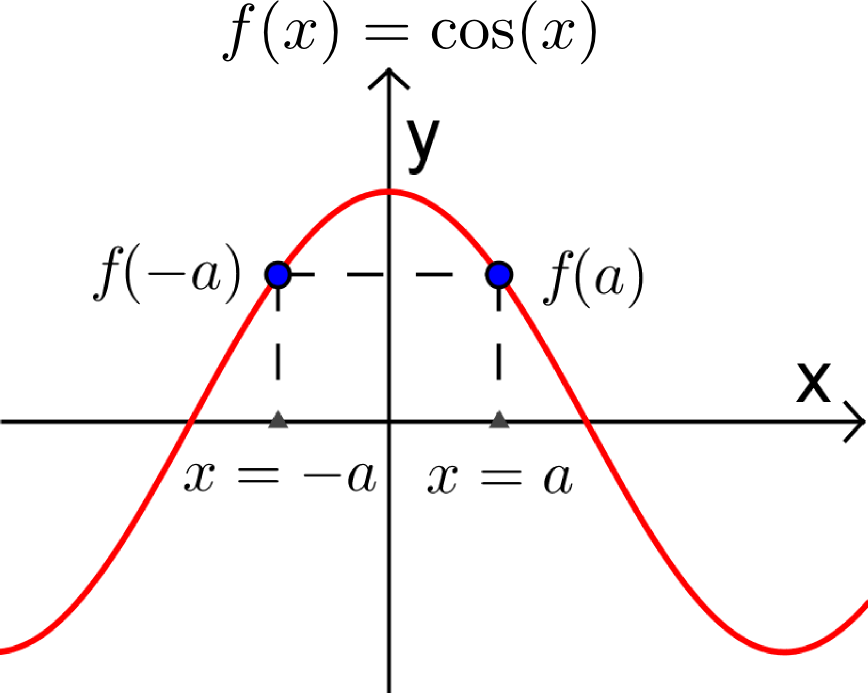
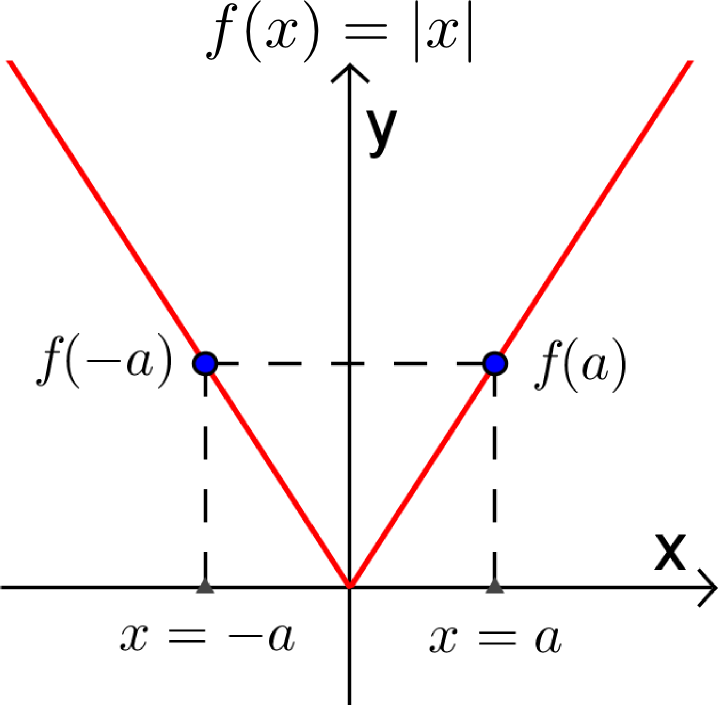
Les fonctions paires et impaires sont des fonctions dont la représentation graphique possède une certaine symétrie.
Il existe plusieurs fonctions de base qui sont des fonctions paires, comme par exemple 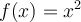 ,
, 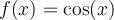 et
et 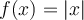 .
.
Exemple : Vérifier que la fonction 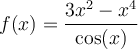 est une fonction paire.
est une fonction paire.
Solution Pour que  soit une fonction paire, elle doit satisfaire l'égalité
soit une fonction paire, elle doit satisfaire l'égalité 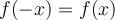 .
.
Vérifions
L'égalité est démontrée.
Les fonctions 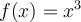 et
et 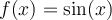 sont des fonctions de base impaires.
sont des fonctions de base impaires.
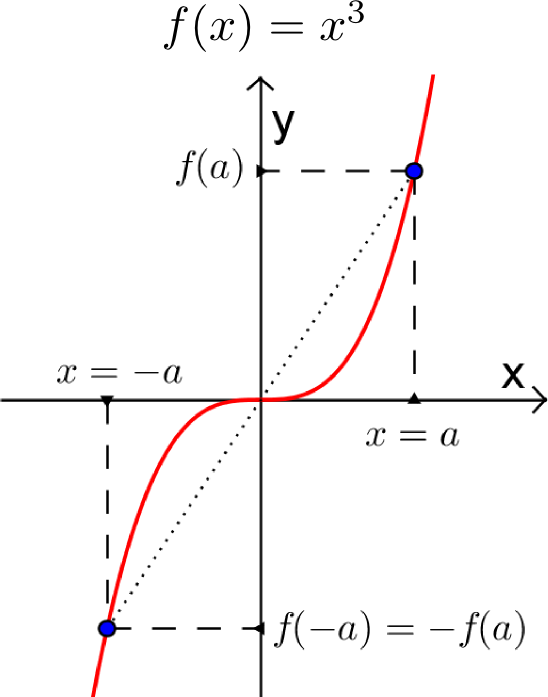
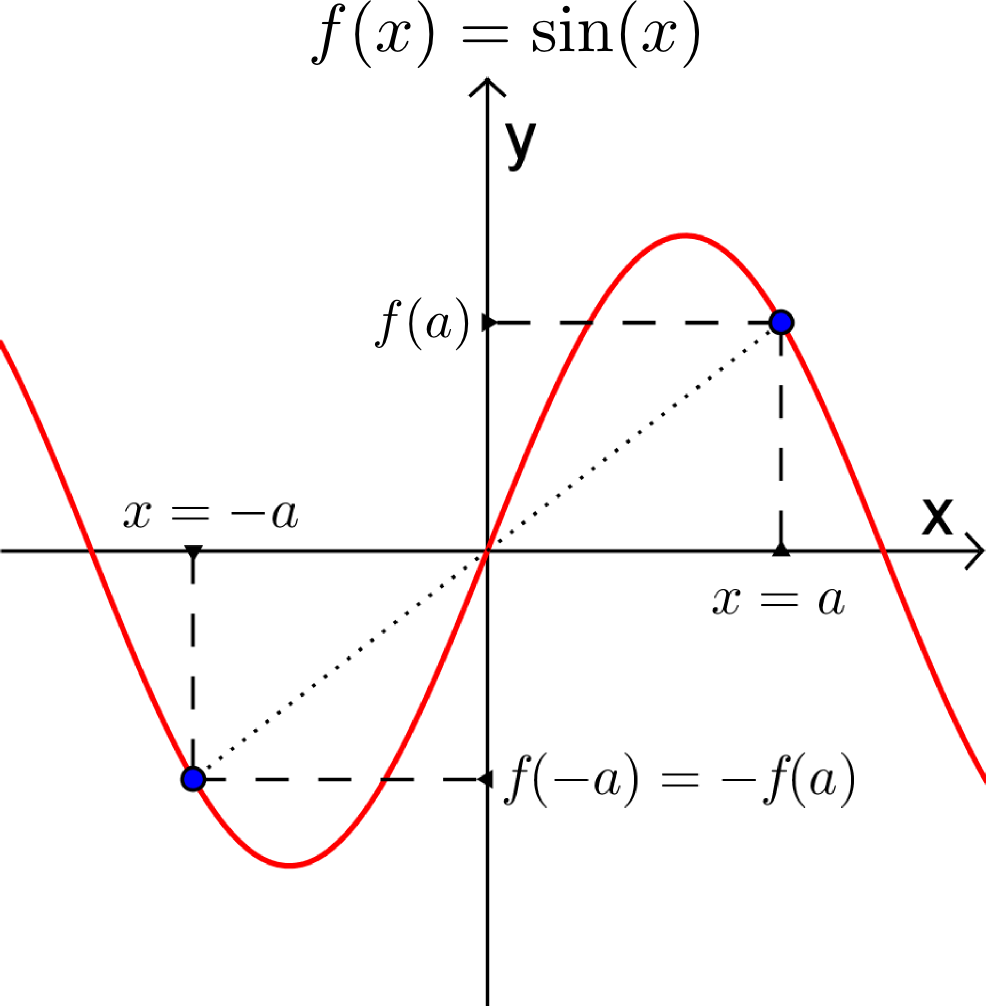
Il faut bien réaliser qu'une fonction n'est pas nécessairement paire ou impaire. En effet, il existe une infinité de fonctions qui ne sont ni paires ni impaires, car elles ne vérifient aucune des deux égalités ci-dessus.
Exemples : Déterminer si les fonctions suivantes sont paires, impaires ou si elles ne sont ni paires ni impaires.
Solution Il faut tout d'abord déterminer la valeur de 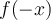 . Si
. Si 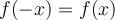 , la fonction est paire, si
, la fonction est paire, si 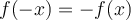 , la fonction est impaire et si on n'obtient aucune des deux égalités précédentes, la fonction n'est ni paire ni impaire.
, la fonction est impaire et si on n'obtient aucune des deux égalités précédentes, la fonction n'est ni paire ni impaire.
Vérifions,
Étant donné que 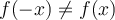 puisque
puisque 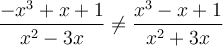 , on peut conclure que la fonction n'est pas paire.
, on peut conclure que la fonction n'est pas paire.
De plus 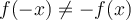 puisque
puisque 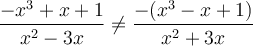 , alors la fonction n'est pas impaire.
, alors la fonction n'est pas impaire.
Par conséquent, la fonction n'est ni paire ni impaire.
Solution Tout comme dans la démarche précédente, il faut déterminer la valeur de 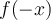 .
.
Calculons,
Voici un graphique Geogebra représentant la fonction paire et la fonction impaire des exemples précédents : 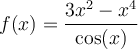 et
et 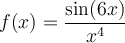 .
.
![]() Cliquez sur la case fonction paire ou fonction impaire pour voir apparaître la fonction de votre choix. Remarquez la symétrie qui existe dans chacun des graphiques. En déplaçant le curseur a, vous déplacez les points symétriques sur la courbe de la fonction.
Cliquez sur la case fonction paire ou fonction impaire pour voir apparaître la fonction de votre choix. Remarquez la symétrie qui existe dans chacun des graphiques. En déplaçant le curseur a, vous déplacez les points symétriques sur la courbe de la fonction.
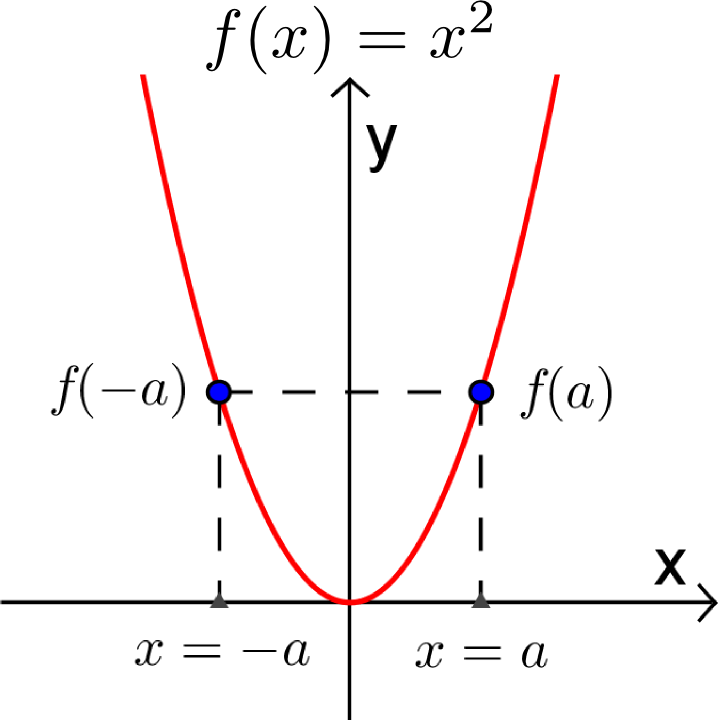
- Sur la fonction paire, pour une valeur de x=a donnée, l'image f(a) et l'image de son opposé f(-a) sont égales.
- Sur la fonction impaire, pour une valeur de x=a donnée, l'image f(a) et l'image de son opposé f(-a) sont opposées, donc de signe contraire.

![\begin{array}{lll}f(-x)&=\dfrac{3(-x)^2-(-x)^4}{\cos(-x)}&\small\text{; on remplace la variable par }-x\\[1em]&=\dfrac{3x^2-x^4}{\cos(x)}&\small\text{; car }(-x)^n=x^n\text{ si }n\text{ est un entier pair}\\[-1em]&&\;\small\text{ et }\cos(-x)=\cos(x)\text{ car cosinus est}\\[-0.5em]&&\;\small\text{ une fonction paire}\\&=f(x)&\end{array} \begin{array}{lll}f(-x)&=\dfrac{3(-x)^2-(-x)^4}{\cos(-x)}&\small\text{; on remplace la variable par }-x\\[1em]&=\dfrac{3x^2-x^4}{\cos(x)}&\small\text{; car }(-x)^n=x^n\text{ si }n\text{ est un entier pair}\\[-1em]&&\;\small\text{ et }\cos(-x)=\cos(x)\text{ car cosinus est}\\[-0.5em]&&\;\small\text{ une fonction paire}\\&=f(x)&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/fb38af90243a039e710820f1c6a99011.png)
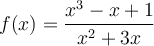
![\begin{array}{ll}f(-x)&=\dfrac{(-x)^3-(-x)+1}{(-x)^2+3(-x)}\\[0.8em]&=\dfrac{-x^3+x+1}{x^2-3x}\end{array} \begin{array}{ll}f(-x)&=\dfrac{(-x)^3-(-x)+1}{(-x)^2+3(-x)}\\[0.8em]&=\dfrac{-x^3+x+1}{x^2-3x}\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/3cb9dc5e2da5615840e34c7ccb217ee0.png)
![\begin{array}{lll}f(-x)&=\dfrac{\sin(-6x)}{(-x)^4}&\\[0.8em]&=\dfrac{-\sin(6x)}{x^4}&\small\text{; car sinus est une fonction impaire}\\[-0.5em]&&\;\small\text{ et }(-x)^4=x^4\\&=-\left(\dfrac{\sin(6x)}{x^4}\right)&\small\text{; mise en évidence de -1}\\&=-f(x)&\end{array} \begin{array}{lll}f(-x)&=\dfrac{\sin(-6x)}{(-x)^4}&\\[0.8em]&=\dfrac{-\sin(6x)}{x^4}&\small\text{; car sinus est une fonction impaire}\\[-0.5em]&&\;\small\text{ et }(-x)^4=x^4\\&=-\left(\dfrac{\sin(6x)}{x^4}\right)&\small\text{; mise en évidence de -1}\\&=-f(x)&\end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0abe1a49d00a6727a4cc5bf730147ad9.png)