2.3 Quelques fonctions particulières
- Fonction définie par parties ou par morceaux
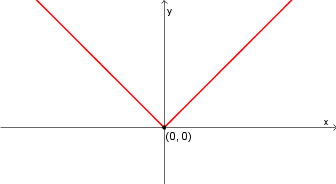
- Fonction valeur absolue
- Fonctions paires et impaires
2. Fonction valeur absolue
On peut remarquer que les caractéristiques principales de cette fonction sont:
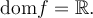
- La fonction possède un seul zéro en
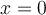 .
. - Elle admet un sommet au point
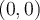 .
. - Cette fonction n'est jamais négative, donc
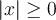 sur son domaine.
sur son domaine.
Il est possible de transformer la fonction valeur absolue de base en une fonction valeur absolue définie par
Explorons les caractéristiques de cette fonction à l'aide du graphique Geogebra suivant.
![]() Déplacez les différents curseurs « a », « b », « h » et « k ».
Déplacez les différents curseurs « a », « b », « h » et « k ».
- Le paramètre
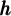 fait subir à la fonction
fait subir à la fonction 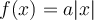 un déplacement horizontal et le paramètre
un déplacement horizontal et le paramètre 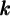 , un déplacement vertical.
, un déplacement vertical. - Le graphique admet pour axe de symétrie la droite
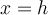 . De plus, le sommet de la fonction est le point
. De plus, le sommet de la fonction est le point 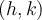 .
. - Le paramètre
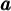 déforme la fonction
déforme la fonction 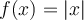 en la contractant ou en la dilatant. De plus, si
en la contractant ou en la dilatant. De plus, si  est négatif, la courbe subit une réflexion par rapport à l'axe des
est négatif, la courbe subit une réflexion par rapport à l'axe des  .
. - Par conséquent, si
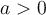 , le sommet
, le sommet 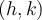 de la fonction est un minimum et si
de la fonction est un minimum et si  , le sommet est un maximum.
, le sommet est un maximum. - Le paramètre
 déforme également la fonction
déforme également la fonction 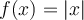 . Par contre, si
. Par contre, si 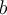 est négatif, la courbe ne subit aucune réflexion par rapport à l'axe des
est négatif, la courbe ne subit aucune réflexion par rapport à l'axe des  . Étant donné que
. Étant donné que 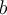 est à l'intérieur de la valeur absolue, il n'influence pas le signe de la fonction, c'est-à-dire que
est à l'intérieur de la valeur absolue, il n'influence pas le signe de la fonction, c'est-à-dire que 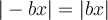 .
.
![]() Exemple : Étudions la fonction
Exemple : Étudions la fonction 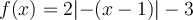 , où
, où 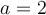 ,
, 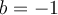 ,
, 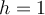 et
et 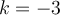 . Par simplification, on peut voir que cette fonction a également pour équation :
. Par simplification, on peut voir que cette fonction a également pour équation :
Le graphique est ouvert vers le haut, car 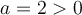 .
.
De plus, le sommet de la fonction est un minimum avec des coordonnées de 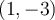 .
.
Pour déterminer les zéros de  , il faut résoudre l'équation
, il faut résoudre l'équation 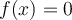 . En utilisant la démarche de résolution d'équations vue dans cette à la section 1.4, on doit résoudre :
. En utilisant la démarche de résolution d'équations vue dans cette à la section 1.4, on doit résoudre :
Finalement, on peut déterminer le signe de la fonction à l'aide du graphique. On a que  est positive sur l'intervalle
est positive sur l'intervalle ![\left]{-\infty,-\frac{1}{2}}\right[ \cup \left]{\frac{5}{2},\infty}\right[ \left]{-\infty,-\frac{1}{2}}\right[ \cup \left]{\frac{5}{2},\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/91b05ad5db6009388403dbd73e3f7c00.png) et
et  est négative sur l'intervalle
est négative sur l'intervalle ![\left]{-\frac{1}{2},\frac{5}{2}}\right[ \left]{-\frac{1}{2},\frac{5}{2}}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/a8bc9bf15dfa25040a6a6e1dcefd9759.png) .
.
Il est aussi intéressant d'étudier les graphiques des fonctions composées de la forme
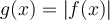
où 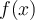 est une fonction quadratique.
est une fonction quadratique.
Le graphique d'une telle fonction n'a plus la forme habituelle d'un « V », car il dépend de la fonction qui est à l'intérieur de la valeur absolue. Par contre, la fonction reste quand même positive sur l'ensemble de son domaine.
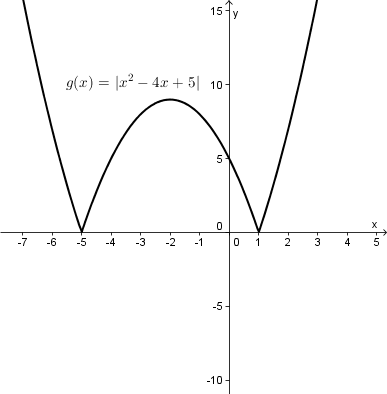
Exemple : Traçons le graphique de la fonction 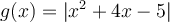 .
.
Étant donné que 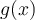 prend toujours des valeurs positives ou nulles, il faut déterminer les valeurs de
prend toujours des valeurs positives ou nulles, il faut déterminer les valeurs de  qui rendent négatif le polynôme à l'intérieur de la valeur absolue. Ainsi, on va étudier le signe du polynôme
qui rendent négatif le polynôme à l'intérieur de la valeur absolue. Ainsi, on va étudier le signe du polynôme 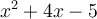 .
.
En factorisant, on obtient 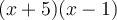 . Les zéros sont donc
. Les zéros sont donc 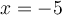 et
et 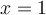 . Construisons un tableau de signes.
. Construisons un tableau de signes.
![\left]{-\infty,-5}\right[ \left]{-\infty,-5}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/592269c20cc54f7b02fd3f460a80193a.png) |
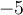 |
![\left]{-5,1}\right[ \left]{-5,1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e73071bfb801a11766a661c79e5425d3.png) |
 |
![\left]{1,\infty}\right[ \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1c8404c763714ff8de9f14e488b459df.png) |
|
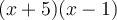 |
 |
 |
 |
 |
 |
Par conséquent,
Nous pouvons donc réécrire l'équation de la fonction  à partir de la définition de la fonction valeur absolue de la façon suivante :
à partir de la définition de la fonction valeur absolue de la façon suivante :
Nous pouvons maintenant traçer ces deux paraboles dans leur intervalle de définition. Sur le graphique de gauche, 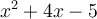 est représentée par la parabole en rouge et
est représentée par la parabole en rouge et 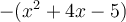 par la parabole en bleu. Par conséquent, en prenant seulement le tracé de ces courbes qui se situe au-dessus de l'axe des
par la parabole en bleu. Par conséquent, en prenant seulement le tracé de ces courbes qui se situe au-dessus de l'axe des  (positif), on obtient le graphique de la fonction
(positif), on obtient le graphique de la fonction 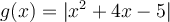 illustré à droite.
illustré à droite.

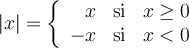
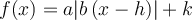
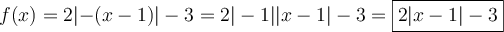
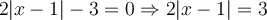
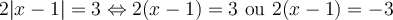
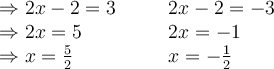
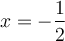
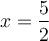
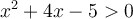
![\left]{-\infty,-5}\right[ \cup \left]{1,\infty}\right[ \left]{-\infty,-5}\right[ \cup \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/ca6a9aa733291a06cfd9266984feebdc.png)
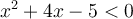
![\left]{-5,1}\right[ \left]{-5,1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6f35e945c2467f69e34d2349576f11ba.png)
![\lvert{x^2+4x-5}\rvert = \left\{\begin{array}{ll}x^2+4x-5&\text{si } x \leq -5 \text{ ou } x \geq 1 \\[0.8em] -(x^2+4x-5) & \text{si } -5 < x < 1 \end{array}\right. \lvert{x^2+4x-5}\rvert = \left\{\begin{array}{ll}x^2+4x-5&\text{si } x \leq -5 \text{ ou } x \geq 1 \\[0.8em] -(x^2+4x-5) & \text{si } -5 < x < 1 \end{array}\right.](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e5cc5f8855cf9d5e3ec6c6a90cbd3ce7.png)