2.2 Les fonctions algébriques
- Fonction linéaire (droite)
- Fonction quadratique (parabole)
- Fonction puissance (exposant naturel)
- Fonction rationnelle
- Fonction racine et exposant fractionnaire
- Trouver le domaine d'une fonction algébrique
6. Trouver le domaine d'une fonction algébrique
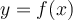 , l'ensemble des éléments
, l'ensemble des éléments  possédant une image réelle
possédant une image réelle  forment le domaine de la fonction
forment le domaine de la fonction  .
.Pour trouver le domaine d'une fonction algébrique quelconque, il faut toujours s'assurer de respecter ces deux restrictions. Voici quelques exemples.
Exemples : Trouvons le domaine des fonctions suivantes.
Le domaine de cette fonction dépend des deux restrictions suivantes :
-
Le dénominateur doit être non nul, c'est-à-dire
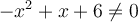 . Trouvons ces valeurs en factorisant :
. Trouvons ces valeurs en factorisant : -
L'expression à l'intérieur de la racine carrée doit être non-négative, c'est-à-dire
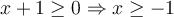 .
.

En combinant ces deux restrictions (voir la droite des réels ci-dessus), on obtient le domaine de  , soit
, soit ![\text{dom }f = \left[-1,3\right[ \cup \left] 3, \infty \right[ \text{dom }f = \left[-1,3\right[ \cup \left] 3, \infty \right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/9e06f3805607c907e8a6b502aa725815.png) . On remarque que
. On remarque que 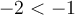 et il s'agit donc d'une valeur qui est déjà enlevée à cause de la deuxième restriction.
et il s'agit donc d'une valeur qui est déjà enlevée à cause de la deuxième restriction.
Voici un dernier exemple de détermination du domaine d'une fonction algébrique où nous avons recours à un tableau de signes pour résoudre une inéquation. Pour revoir les notions théoriques sur cette méthode, visitez la page « Résoudre une inéquation à l'aide d'un tableau de signes ».
Pour respecter la première restriction, il faut résoudre l'inéquation 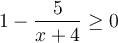 . En transformant cette inéquation sous la forme
. En transformant cette inéquation sous la forme 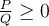 , on obtient :
, on obtient :
Sachant que le numérateur 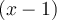 est nul si
est nul si 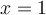 et que le dénominateur
et que le dénominateur 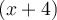 est nul si
est nul si 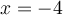 , on peut remplir le tableau de signes suivant pour résoudre l'inéquation.
, on peut remplir le tableau de signes suivant pour résoudre l'inéquation.
![\left]{-\infty,-4}\right[ \left]{-\infty,-4}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/c4873b204332e00af88b94a6d93340db.png) |
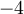 |
![\left]{-4,1}\right[ \left]{-4,1}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d853a16c2f5c3a62322fa6fe5407431a.png) |
 |
![\left]{1,\infty}\right[ \left]{1,\infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1c8404c763714ff8de9f14e488b459df.png) |
|
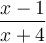 |
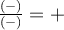 |
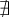 |
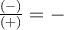 |
 |
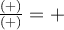 |
On obtient que ![\text{dom }f = \left]-\infty,-4\right[ \cup \left[1,\infty\right[ \text{dom }f = \left]-\infty,-4\right[ \cup \left[1,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7f2f97ff3a8115673a621ef4df7906e9.png) . On remarque que
. On remarque que 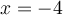 n'appartient pas au domaine de
n'appartient pas au domaine de  cette valeur entraîne un dénominateur nul.
cette valeur entraîne un dénominateur nul.
Voici un graphique Geogebra pour illustrer la fonction et le calcul d'images pour certaines valeurs de  .
. ![]() Déplacez le curseur b avec votre souris pour voir la valeur de l'image f(b). En même temps, le point bleu
Déplacez le curseur b avec votre souris pour voir la valeur de l'image f(b). En même temps, le point bleu 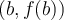 se déplace sur la courbe de la fonction
se déplace sur la courbe de la fonction 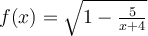 . Remarquez les valeurs de b qui font partie du domaine de
. Remarquez les valeurs de b qui font partie du domaine de  .
.
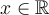
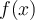
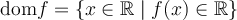
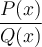
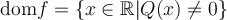
![\sqrt[n]{H(x)} \sqrt[n]{H(x)}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/2e4f25b82acfaae56935615e04f58357.png)
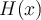
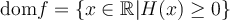
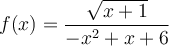
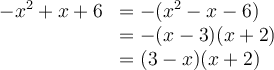
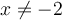
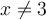
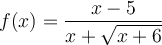
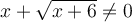
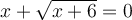

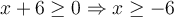
![\text{dom }f = \left[-6,-2\right[ \cup \left] -2,\infty\right[ \text{dom }f = \left[-6,-2\right[ \cup \left] -2,\infty\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/6e01a1f84912e669f9112d32c5c0df09.png)
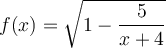
![\begin{array}{ll} 1-\dfrac{5}{x+4} \geq 0 & \Rightarrow \dfrac{(x+4)-5}{x+4} \geq 0\\[0.8em] &\Rightarrow \dfrac{x-1}{x+4} \geq 0 \end{array} \begin{array}{ll} 1-\dfrac{5}{x+4} \geq 0 & \Rightarrow \dfrac{(x+4)-5}{x+4} \geq 0\\[0.8em] &\Rightarrow \dfrac{x-1}{x+4} \geq 0 \end{array}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/7ba927fa01b6527924a868bd54114acd.png)