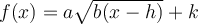2.2 Les fonctions algébriques
- Fonction linéaire (droite)
- Fonction quadratique (parabole)
- Fonction puissance (exposant naturel)
- Fonction rationnelle
- Fonction racine et exposant fractionnaire
- Trouver le domaine d'une fonction algébrique
5. Fonction racine et exposant fractionnaire
Comme nous avons vu dans une section précédente, les fonctions de la forme 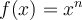 sont appelées fonctions puissances. Si l'exposant est un nombre fractionnaire, cela signifie que la fonction est irrationnelle et, dans son équation, la variable indépendante apparaît sous un radical.
sont appelées fonctions puissances. Si l'exposant est un nombre fractionnaire, cela signifie que la fonction est irrationnelle et, dans son équation, la variable indépendante apparaît sous un radical.
Voici la définition et le graphique de quelques fonctions à exposant fractionnaire.
![f(x) = x^{1/3} = \sqrt[3]{x} f(x) = x^{1/3} = \sqrt[3]{x}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/1f88f99349b9b43ffb704dfc00690fdb.png) 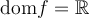 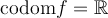 |
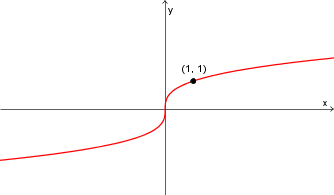 |
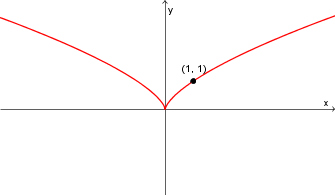
![f(x) = x^{2/3} = \sqrt[3]{x^2} f(x) = x^{2/3} = \sqrt[3]{x^2}](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cf72359649a6fb5f3a0fb6ad5cb7fb21.png) 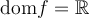 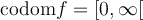 |
 |
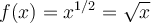 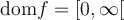 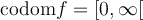 |
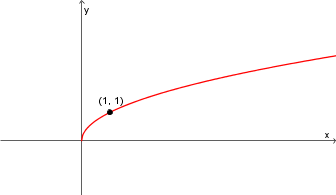 |
Étudions plus en détail cette dernière fonction, soit la fonction racine carrée
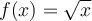 . Pour définir la fonction racine carrée, on peut faire appel à la réciproque de la fonction quadratique
. Pour définir la fonction racine carrée, on peut faire appel à la réciproque de la fonction quadratique 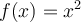 . Ce sujet est abordé dans une autre section. Contentons-nous d'explorer les caractéristiques de la fonction racine à partir du graphique GeoGebra suivant.
. Ce sujet est abordé dans une autre section. Contentons-nous d'explorer les caractéristiques de la fonction racine à partir du graphique GeoGebra suivant.La fonction racine carrée de base 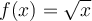 possède les caractéristiques suivantes:
possède les caractéristiques suivantes:
- La fonction possède un seul zéro en
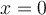 et il s'agit d'un minimum.
et il s'agit d'un minimum. - Elle est croissante sur tout son domaine, soit sur
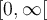 .
. - Elle est positive sur
![\left]{0, \infty}\right[ \left]{0, \infty}\right[](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/d13a6e4c304d2f4a427dad83ef19750a.png) et nulle si
et nulle si 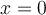 . Elle n'est jamais négative.
. Elle n'est jamais négative.
On peut également créer d'autres fonctions composées à partir de la fonction racine de base. Nous élaborerons ce concept plus en détails dans la section sur les transformations de fonctions. Pour l'instant, dans le graphique Geogebra, on s'intéresse aux fonctions de la forme
![]() Déplacez les différents curseurs « a », « b », « h » et « k ».
Déplacez les différents curseurs « a », « b », « h » et « k ».
- Le paramètre
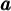 déforme verticalement la fonction racine de base. De plus, si
déforme verticalement la fonction racine de base. De plus, si  change de signe, la courbe subit une réflexion par rapport à l'axe des
change de signe, la courbe subit une réflexion par rapport à l'axe des 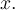
- Le paramètre
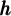 fait subir à la fonction
fait subir à la fonction 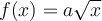 une translation horizontale et le paramètre
une translation horizontale et le paramètre 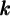 , une translation verticale.
, une translation verticale. - Si
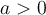 , le point
, le point 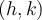 est un minimum et si
est un minimum et si  , le point
, le point 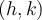 est un maximum.
est un maximum. - Le paramètre
 déforme horizontalement la fonction racine de base. Par contre, si
déforme horizontalement la fonction racine de base. Par contre, si 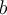 change de signe, la courbe subit une réflexion par rapport à la droite verticale passant par le sommet
change de signe, la courbe subit une réflexion par rapport à la droite verticale passant par le sommet 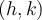 .
. - La règle de transformation appliquée au graphique de la fonction de base est :
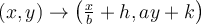 . Tous les points
. Tous les points 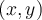 de la fonction
de la fonction 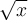 sont transformés par cette règle.
sont transformés par cette règle.
Dans le graphique Geogebra, cela est illustré par le point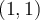 de la fonction
de la fonction 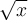 pointillée qui s'est déplacé au point P.
pointillée qui s'est déplacé au point P.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 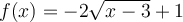 .
.
On a que 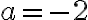 et
et 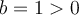 . La courbe est donc décroissante, car elle a subit une réflexion verticale. On remarque aussi que tous les points du graphique
. La courbe est donc décroissante, car elle a subit une réflexion verticale. On remarque aussi que tous les points du graphique 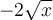 subissent un déplacement vers la droite de
subissent un déplacement vers la droite de 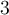 et vers le haut de
et vers le haut de  . L'extrémité
. L'extrémité 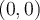 s'est donc déplacé au point
s'est donc déplacé au point 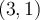 . Il s'agit d'un maximum.
. Il s'agit d'un maximum.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 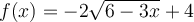 .
.
En effectuant une mise en évidence, on a que 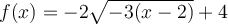 . Ainsi,
. Ainsi, 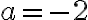 et
et 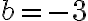 . La courbe est donc croissante, car elle a subit une réflexion verticale et une réflexion horizontale. De plus, le sommet
. La courbe est donc croissante, car elle a subit une réflexion verticale et une réflexion horizontale. De plus, le sommet 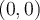 s'est déplacé au point
s'est déplacé au point 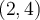 . Il s'agit d'un minimum.
. Il s'agit d'un minimum.