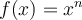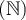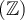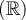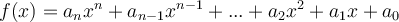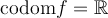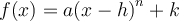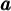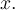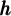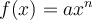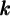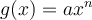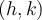2.2 Les fonctions algébriques
- Fonction linéaire (droite)
- Fonction quadratique (parabole)
- Fonction puissance (exposant naturel)
- Fonction rationnelle
- Fonction racine et exposant fractionnaire
- Trouver le domaine d'une fonction algébrique
3. Fonction puissance (exposant naturel)
Si  est un entier négatif, il s'agit de fonctions rationnelles et elles seront traitées dans la prochaine section. Les exposants de la forme
est un entier négatif, il s'agit de fonctions rationnelles et elles seront traitées dans la prochaine section. Les exposants de la forme 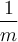 , les fonctions racines, et les exposants réels seront également abordés plus loin. Les fonctions puissances à exposant naturel, celles qui nous intéressent, servent de base dans la construction des fonctions polynomiales de degré
, les fonctions racines, et les exposants réels seront également abordés plus loin. Les fonctions puissances à exposant naturel, celles qui nous intéressent, servent de base dans la construction des fonctions polynomiales de degré  de la forme :
de la forme :
où les coefficients 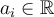 pour tout
pour tout 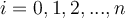 ,
, 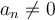 et
et 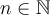 .
.
À partir du graphique GeoGebra suivant, étudions plus en détails les caractéristiques des fonctions puissances pour différentes valeurs de  .
.
Les premières valeurs de  correspondent à des fonctions de base :
correspondent à des fonctions de base :
- Pour
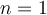 , c'est la fonction linéaire
, c'est la fonction linéaire 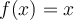 .
. - Pour
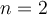 , c'est la fonction quadratique
, c'est la fonction quadratique 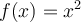 .
. - Pour
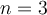 , c'est la fonction cubique
, c'est la fonction cubique 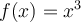 .
. - Si
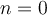 , on aura la fonction constante
, on aura la fonction constante 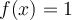 .
.
Toutes ces fonctions ont comme point commun 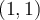 .
. ![]() Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique d'une augmentation ou d'une diminution de l'exposant.
Déplacez le curseur vertical à gauche afin de remarquer l'effet sur le graphique d'une augmentation ou d'une diminution de l'exposant.
On peut séparer les fonctions puissances en deux catégories, selon que l'exposant  est pair ou impair.
est pair ou impair.
- Pour
 pair,
pair, 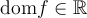
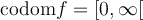 .
.- La fonction possède l'axe des
 comme axe de symétrie.
comme axe de symétrie. - Elle possède un seul zéro en
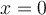 et il s'agit d'un minimum.
et il s'agit d'un minimum. - Pour
 impair,
impair,
On peut également créer d'autres fonctions composées à partir des fonctions puissances de base. Nous élaborerons ce concept plus en détail dans la section sur les transformations de fonctions. Pour l'instant, dans le graphique Geogebra, on s'intéresse aux fonctions de la forme
![]() Déplacez les différents curseurs « a », « h » et « k ».
Déplacez les différents curseurs « a », « h » et « k ».
![]() Ex. : Choisissez la fonction de base
Ex. : Choisissez la fonction de base 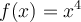 . Si
. Si 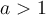 , la fonction décroit et croit plus rapidement que la fonction
, la fonction décroit et croit plus rapidement que la fonction 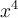 (la courbe se comprime sur l'axe des
(la courbe se comprime sur l'axe des  ). Si
). Si 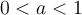 , la fonction décroit et croit moins rapidement. De plus, pour
, la fonction décroit et croit moins rapidement. De plus, pour 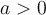 , la fonction est positive et pour
, la fonction est positive et pour 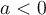 , la fonction est négative.
, la fonction est négative.
![]() Ex. : Choisissez la fonction
Ex. : Choisissez la fonction 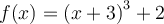 . On remarque le graphique de la fonction de base
. On remarque le graphique de la fonction de base 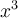 subit un déplacement vers la gauche de
subit un déplacement vers la gauche de 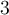 et vers le haut de
et vers le haut de 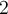 . Donc le point
. Donc le point 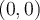 s'est déplacé au point
s'est déplacé au point 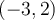 .
.
Par conséquent, on peut généraliser les résultats précédents.