3.3 Fonctions trigonométriques inverses
- Introduction
- Fonction arcsin
- Fonction arccos
- Fonction arctan
- Autres fonctions trigonométriques inverses
- Résoudre une équation trigonométrique
3. Fonction arccos
De la même manière que la fonction arcsinus, la fonction arccosinus est la réciproque d'une fonction injective cosinus définie sur un domaine restreint. En effet, on constate que la fonction 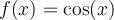 définie sur
définie sur 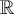 n'est pas injective, et par conséquent sa courbe réciproque n'est pas celle d'une fonction.
n'est pas injective, et par conséquent sa courbe réciproque n'est pas celle d'une fonction.
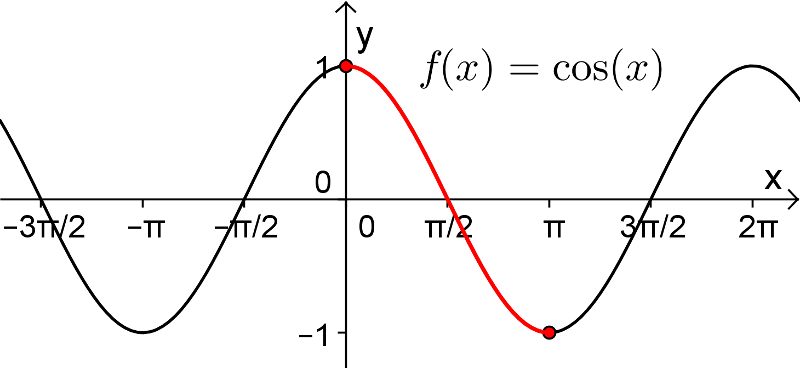

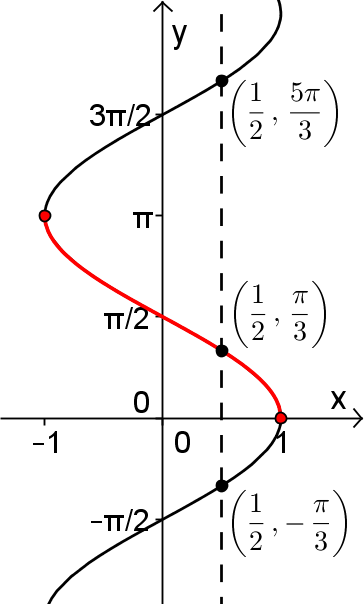
Par convention, c'est sur l'intervalle des valeurs ![x\in\left[0,\pi\right] x\in\left[0,\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/e28905bc597d51e5f27a8e9b597f21b6.png) qu'est définie notre fonction injective
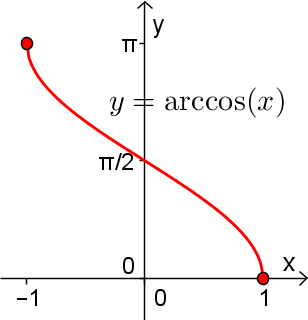
qu'est définie notre fonction injective 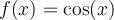 , représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arccosinus de la façon suivante.
, représentée par la courbe rouge ci-dessus. Nous pouvons alors définir la fonction arccosinus de la façon suivante.
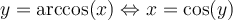
![y\in\left[0,\pi\right] y\in\left[0,\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/0558feb0113ff6831af2332059a18985.png)
![\text{dom}(\arccos)=[-1,1] \text{dom}(\arccos)=[-1,1]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/76dcfaae0d48271dfb85d15877de31b4.png)
![\text{ima}(\arccos)=\left[0,\pi\right] \text{ima}(\arccos)=\left[0,\pi\right]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/16a45cf9c303248688c1d3428f7a806a.png)
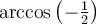
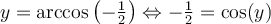
![y\in [0,\pi] y\in [0,\pi]](https://mathematic.moodle.decclic.qc.ca/filter/tex/pix.php/cf1f64a90a341c31ef34ddfd24c671ba.png)